Theory and Applications of Boosting
Rob Schapire

Example: How May I Help You?

[Gorin et al.]

goal: automatically categorize type of call requested by phone customer (Collect, CallingCard, PersonToPerson, etc.) yes Id like to place a collect call long distance please (Collect) operator I need to make a call but I need to bill it to my office (ThirdNumber) yes Id like to place a call on my master card please (CallingCard) I just called a number in sioux city and I musta rang the wrong number because I got the wrong party and I would like to have that taken off of my bill (BillingCredit) observation:

easy to nd rules of thumb that are often correct e.g.: IF card occurs in utterance THEN predict CallingCard hard to nd single highly accurate prediction rule

The Boosting Approach

devise computer program for deriving rough rules of thumb apply procedure to subset of examples obtain rule of thumb apply to 2nd subset of examples obtain 2nd rule of thumb repeat T times

Key Details

how to choose examples on each round?

concentrate on hardest examples (those most often misclassied by previous rules of thumb) take (weighted) majority vote of rules of thumb

how to combine rules of thumb into single prediction rule?

Boosting

boosting = general method of converting rough rules of

thumb into highly accurate prediction rule
technically:

assume given weak learning algorithm that can consistently nd classiers (rules of thumb) at least slightly better than random, say, accuracy 55% (in two-class setting) [ weak learning assumption ] given sucient data, a boosting algorithm can provably construct single classier with very high accuracy, say, 99%

Outline of Tutorial

basic algorithm and core theory fundamental perspectives practical extensions advanced topics

Preamble: Early History

Strong and Weak Learnability
boostings roots are in PAC learning model strong PAC learning algorithm:

[Valiant 84]

get random examples from unknown, arbitrary distribution

for any distribution with high probability given polynomially many examples (and polynomial time) can nd classier with arbitrarily small generalization error same, but generalization error only needs to be slightly better than random guessing ( 1 ) 2 does weak learnability imply strong learnability?

weak PAC learning algorithm

[Kearns & Valiant 88]:

If Boosting Possible, Then...

can use (fairly) wild guesses to produce highly accurate

predictions
if can learn part way then can learn all the way should be able to improve any learning algorithm for any learning problem:

either can always learn with nearly perfect accuracy or there exist cases where cannot learn even slightly better than random guessing

First Boosting Algorithms

[Schapire 89]:

rst provable boosting algorithm optimal algorithm that boosts by majority rst experiments using boosting limited by practical drawbacks introduced AdaBoost algorithm strong practical advantages over previous boosting algorithms

[Freund 90]:

[Drucker, Schapire & Simard 92]:

[Freund & Schapire 95]:

Basic Algorithm and Core Theory
introduction to AdaBoost analysis of training error analysis of test error

and the margins theory
experiments and applications

Basic Algorithm and Core Theory
introduction to AdaBoost analysis of training error analysis of test error

and the margins theory
experiments and applications

A Formal Description of Boosting

given training set for t = 1, . . . , T :

(x1 , y1 ), . . . , (xm , ym )

yi {1, +1} correct label of instance xi X

construct distribution Dt on {1, . . . , m} nd weak classier (rule of thumb) ht : X {1, +1} with error t on Dt : t = PriDt [ht (xi ) = yi ]

output nal/combined classier Hnal

AdaBoost
constructing Dt :

[with Freund]

D1 (i) = 1/m given Dt and ht : Dt+1 (i) = = Dt (i) e t if yi = ht (xi ) if yi = ht (xi ) e t Zt Dt (i) exp(t yi ht (xi )) Zt

where Zt = normalization factor 1 1 t >0 t = ln 2 t nal classier:

Hnal (x) = sign
t

t ht (x)

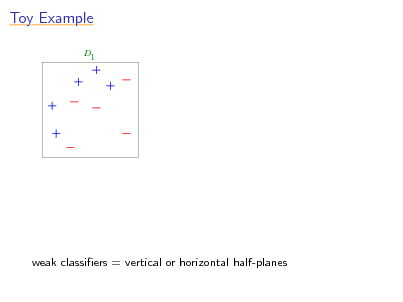
Toy Example
D1

weak classiers = vertical or horizontal half-planes

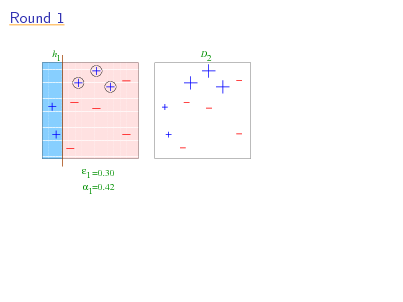
Round 1
1 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 1 =0.30 1=0.42 h D2

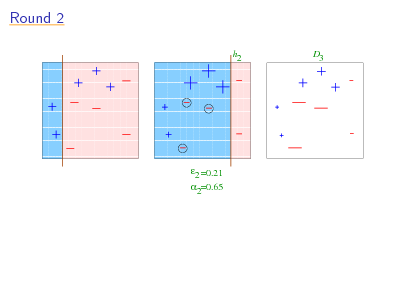
Round 2
11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 1111111111111 2 00000000000001111 11111111111110000 1111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000001111 11111111111110000 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000 11111111111111111 00000000000000000

h

D3

2 =0.21 2=0.65

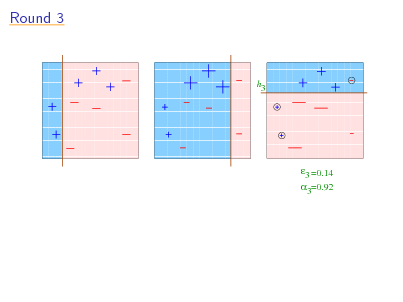
Round 3
11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 11111 1111111111111 00000 0000000000000 11111 00000 1111111111111 0000000000000 11111 00000 1111111111111 0000000000000 11111 1111111111111 00000 0000000000000 1111111111111 00000000000001111 111111111111111 000000000000000 11111111111110000 1111 00000000000000000 111111111111111 000000000000000 11111111111111111 00000000000000000 111111111111111 000000000000000 11111111111111111 000000000000000 00000000000000000 111111111111111 11111111111111111 111111111111111 000000000000000 00000000000000000 11111111111111111 111111111111111 000000000000000 00000000000000000 11111111111111111 111111111111111 00000000000000000 11111111111111111 00000000000000000 h 000000000000000 111111111111111 000000000000000 000000000000000 11111111111111111 00000000000000000 111111111111111 11111111111111111 111111111111111 00000000000000000 3 000000000000000 11111111111111111 00000000000000000 111111111111111 000000000000000 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 111111111111111 000000000000000 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 111111111111111 000000000000000 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 111111111111111 000000000000000 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 111111111111111 000000000000000 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111 11111111111111111 00000000000000000 000000000000000 111111111111111

3 =0.14 3=0.92

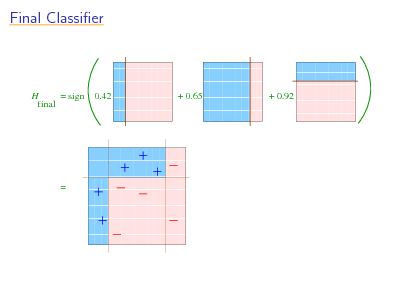
Final Classier
000 000000000 111 111111111 000 000000000 111 111111111 111 000 111111111 000000000 000 000000000 111 111111111 000 000000000 111 111111111 000 000000000 111 111111111 111 000 111111111 000000000 000 000000000 111 111111111 000 000000000 111 111111111 000 000000000 111 111 000 111111111 000000000 0.42 111111111 + 000 000000000 111 111111111 000 000000000 111 111111111 000 000000000 111 111111111 000 000000000 111 111111111 111 000 111111111 000000000 000 000000000 111 111111111 000 000000000 111 111111111 000 000000000 111 111111111 000000000 00 111111111 11 000000000 00 111111111 11 111111111 000000000 11 00 000000000 00 111111111 11 000000000 00 111111111 11 000000000 00 111111111 11 111111111 000000000 11 00 000000000 00 111111111 11 000000000 00 111111111 11 000000000 00 111111111 11 111111111 000000000 11 00 0.65 000000000 00 111111111 11 000000000 00 111111111 11 000000000 00 111111111 11 000000000 00 111111111 11 111111111 000000000 11 00 000000000 00 111111111 11 000000000 00 111111111 11 000000000 00 111111111 11 1111111111 0000000000 1111111111 0000000000 1111111111 0000000000 1111111111 0000000000 1111111111 0000000000 1111111111 0000000000 1111111111 0000000000 1111111111 0000000000 0000000000 1111111111 1111111111 0000000000 1111111111 0000000000 1111111111 0000000000 0000000000 1111111111 1111111111 0000000000 1111111111 0000000000 1111111111 0000000000 1111111111 0000000000 0000000000 1111111111 1111111111 0000000000 1111111111 0000000000

H = sign final

+ 0.92

=

1111111111111 0000000000000 11111 00000 111111111111 000000000000 1111111111111 0000000000000 11111 00000 111111111111 000000000000 1111111111111 0000000000000 11111 00000 111111111111 000000000000 0000000000000 1111111111111 11111 00000 111111111111 000000000000 0000000000000 1111111111111 11111 111111111111 00000 000000000000 1111111111111 0000000000000 11111 00000 111111111111 000000000000 1111111111111 0000000000000 11111 111111111111 00000 000000000000 1111111111111 0000000000000 11111 00000 111111111111 000000000000 1111111111111 0000000000000 11111 111111111111 00000 000000000000 0000000000000 1111111111111 11111 111111111111 00000 000000000000 1111111111111 0000000000000 11111 00000 111111111111 000000000000 11111 111111111111 00000 000000000000 11111 00000 111111111111 000000000000 11111 00000 111111111111 000000000000 11111 111111111111 00000 000000000000 11111 00000 111111111111 000000000000 11111 111111111111 00000 000000000000 11111 111111111111 00000 000000000000 11111 00000 111111111111 000000000000 11111 111111111111 00000 000000000000 11111 00000 111111111111 000000000000 11111 00000 111111111111 000000000000 11111 111111111111 00000 000000000000 11111 00000 111111111111 000000000000 11111 111111111111 00000 000000000000 11111 111111111111 00000 000000000000 11111 00000 111111111111 000000000000 11111 00000 111111111111 000000000000 11111 00000 111111111111 000000000000 11111 111111111111 00000 000000000000 11111 111111111111 00000 000000000000 11111 00000 111111111111 000000000000

Basic Algorithm and Core Theory
introduction to AdaBoost analysis of training error analysis of test error

and the margins theory
experiments and applications

Analyzing the Training Error
Theorem:

[with Freund]

write t as then

1 2

t

[ t = edge ] 2 t (1 t )
t 2 1 4t t

training error(Hnal ) =

exp 2
t

2 t

so: if t : t > 0

then training error(Hnal ) e 2 T AdaBoost is adaptive: does not need to know or T a priori can exploit t

2

Proof
let F (x) =
t

t ht (x) Hnal (x) = sign(F (x))

Step 1: unwrapping recurrence:

Dnal (i) =

1 m

exp yi
t

t ht (xi ) Zt
t

=

1 exp (yi F (xi )) m Zt
t

Proof (cont.)
Step 2: training error(Hnal )
t

Zt

Proof:

training error(Hnal ) =

1 m 1 m 1 m

i

1 if yi = Hnal (xi ) 0 else 1 if yi F (xi ) 0 0 else exp(yi F (xi ))

= =

i

i

Dnal (i)
i t

Zt

=
t

Zt

Proof (cont.)

Step 3: Zt = 2 Proof:

t (1 t )

Zt

=
i

Dt (i) exp(t yi ht (xi )) Dt (i)e t +
i:yi =ht (xi ) t e t + (1

= =

Dt (i)e t

t ) e

i:yi =ht (xi ) t

= 2 t (1 t )

Basic Algorithm and Core Theory
introduction to AdaBoost analysis of training error analysis of test error

and the margins theory
experiments and applications

How Will Test Error Behave? (A First Guess)
1 0.8

error

0.6 0.4 0.2

test train
20 40 60 80 100

# of rounds (T)

expect:
training error to continue to drop (or reach zero) test error to increase when Hnal becomes too complex

Occams razor overtting hard to know when to stop training

Technically...

with high probability:

generalization error training error + O bound depends on m = # training examples d = complexity of weak classiers T = # rounds

dT m

generalization error = E [test error] predicts overtting

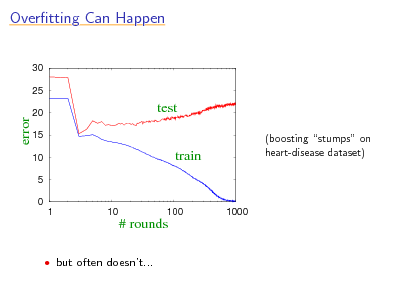
Overtting Can Happen
30 25

error

20 15 10 5 0 1 10

test train
(boosting stumps on heart-disease dataset)

100

1000

# rounds
but often doesnt...

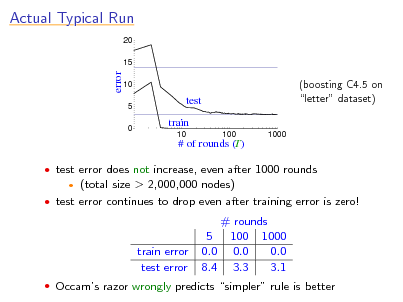
Actual Typical Run
20 15

error

10 5 0

test train
10 100 1000

(boosting C4.5 on letter dataset)

# of rounds (T)
test error does not increase, even after 1000 rounds

(total size > 2,000,000 nodes) test error continues to drop even after training error is zero!

train error test error

# rounds 5 100 1000 0.0 0.0 0.0 8.4 3.3 3.1

Occams razor wrongly predicts simpler rule is better

A Better Story: The Margins Explanation
key idea:

[with Freund, Bartlett & Lee]

training error only measures whether classications are right or wrong should also consider condence of classications

recall: Hnal is weighted majority vote of weak classiers measure condence by margin = strength of the vote

= (weighted fraction voting correctly) (weighted fraction voting incorrectly)
high conf. incorrect 1 Hfinal incorrect high conf. correct Hfinal correct +1

low conf. 0

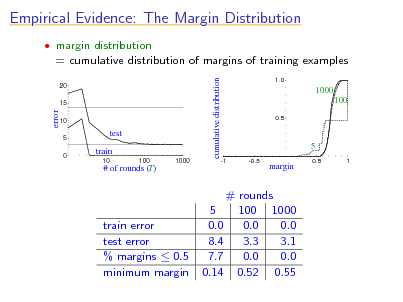
Empirical Evidence: The Margin Distribution
margin distribution

= cumulative distribution of margins of training examples
cumulative distribution
20 15
1.0

1000 100
0.5

error

10 5 0

test train
10 100 1000

5
-1 -0.5

# of rounds (T)

margin

0.5

1

train error test error % margins 0.5 minimum margin

# rounds 5 100 1000 0.0 0.0 0.0 8.4 3.3 3.1 7.7 0.0 0.0 0.14 0.52 0.55

Theoretical Evidence: Analyzing Boosting Using Margins
Theorem: large margins better bound on generalization

error (independent of number of rounds) proof idea: if all margins are large, then can approximate nal classier by a much smaller classier (just as polls can predict not-too-close election)
Theorem: boosting tends to increase margins of training

examples (given weak learning assumption) moreover, larger edges larger margins proof idea: similar to training error proof
so:

although nal classier is getting larger, margins are likely to be increasing, so nal classier actually getting close to a simpler classier, driving down the test error

More Technically...
with high probability, > 0 :

generalization error Pr[margin ] + O

d/m

(Pr[ ] = empirical probability)

bound depends on m = # training examples d = complexity of weak classiers entire distribution of margins of training examples
1 2

Pr[margin ] 0 exponentially fast (in T ) if t <

(t)

so: if weak learning assumption holds, then all examples will quickly have large margins

Consequences of Margins Theory
predicts good generalization with no overtting if:

weak classiers have large edges (implying large margins) weak classiers not too complex relative to size of training set

e.g., boosting decision trees resistant to overtting since trees

often have large edges and limited complexity
overtting may occur if:

small edges (undertting), or overly complex weak classiers

e.g., heart-disease dataset:

stumps yield small edges also, small dataset

Improved Boosting with Better Margin-Maximization?

can design algorithms more eective than AdaBoost at

maximizing the minimum margin
in practice, often perform worse why?? more aggressive margin maximization seems to lead to: [Breiman]

more complex weak classiers (even using same weak learner); or higher minimum margins, but margin distributions that are lower overall

[with Reyzin]

Comparison to SVMs

both AdaBoost and SVMs:

work by maximizing margins nd linear threshold function in high-dimensional space

dierences:

margin measured slightly dierently (using dierent norms) SVMs handle high-dimensional space using kernel trick; AdaBoost uses weak learner to search over space SVMs maximize minimum margin; AdaBoost maximizes margin distribution in a more diuse sense

Basic Algorithm and Core Theory
introduction to AdaBoost analysis of training error analysis of test error

and the margins theory
experiments and applications

Practical Advantages of AdaBoost
fast simple and easy to program no parameters to tune (except T ) exible can combine with any learning algorithm no prior knowledge needed about weak learner provably eective, provided can consistently nd rough rules

of thumb shift in mind set goal now is merely to nd classiers barely better than random guessing
versatile

can use with data that is textual, numeric, discrete, etc. has been extended to learning problems well beyond binary classication

Caveats

performance of AdaBoost depends on data and weak learner consistent with theory, AdaBoost can fail if

weak classiers too complex overtting weak classiers too weak (t 0 too quickly) undertting low margins overtting

empirically, AdaBoost seems especially susceptible to uniform

noise

UCI Experiments
tested AdaBoost on UCI benchmarks used:

[with Freund]

C4.5 (Quinlans decision tree algorithm) decision stumps: very simple rules of thumb that test on single attributes

eye color = brown ? yes predict +1 no predict -1

height > 5 feet ? yes predict -1 no predict +1

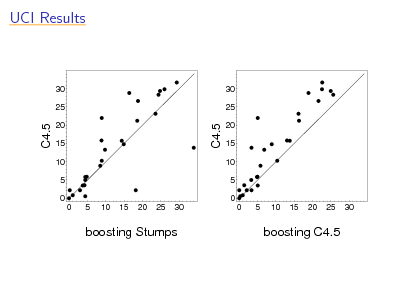
UCI Results

30 25

30 25

C4.5

C4.5

20 15 10 5 0 0 5 10 15 20 25 30

20 15 10 5 0 0 5 10 15 20 25 30

boosting Stumps

boosting C4.5

Application: Detecting Faces

[Viola & Jones]

problem: nd faces in photograph or movie weak classiers: detect light/dark rectangles in image

many clever tricks to make extremely fast and accurate

Application: Human-Computer Spoken Dialogue

[with Rahim, Di Fabbrizio, Dutton, Gupta, Hollister & Riccardi]

application: automatic store front or help desk for AT&T

Labs Natural Voices business
caller can request demo, pricing information, technical

support, sales agent, etc.
interactive dialogue

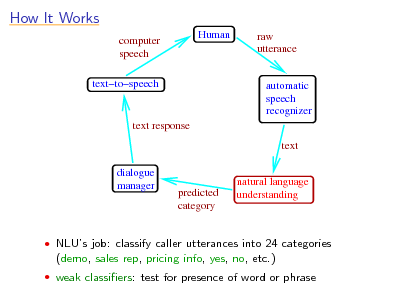
How It Works
computer speech texttospeech Human raw utterance

automatic speech recognizer text

text response

dialogue manager

predicted category

natural language understanding

NLUs job: classify caller utterances into 24 categories

(demo, sales rep, pricing info, yes, no, etc.)
weak classiers: test for presence of word or phrase

Problem: Labels are Expensive

for spoken-dialogue task

getting examples is cheap getting labels is expensive must be annotated by humans

how to reduce number of labels needed?

Active Learning

[with Tur & Hakkani-Tr] u

idea:

use selective sampling to choose which examples to label focus on least condent examples [Lewis & Gale]

for boosting, use (absolute) margin as natural condence measure [Abe & Mamitsuka]

Labeling Scheme

start with pool of unlabeled examples choose (say) 500 examples at random for labeling run boosting on all labeled examples

get combined classier F choose examples with minimum |F (x)| (proportional to absolute margin)

pick (say) 250 additional examples from pool for labeling

repeat

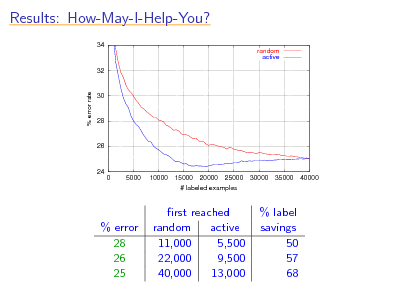
Results: How-May-I-Help-You?
34 random active

32

% error rate

30

28

26

24 0 5000 10000 15000 20000 25000 # labeled examples 30000 35000 40000

% error 28 26 25

rst reached random active 11,000 5,500 22,000 9,500 40,000 13,000

% label savings 50 57 68

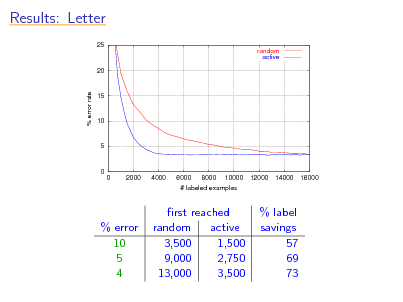
Results: Letter
25 random active

20

% error rate

15

10

5

0 0 2000 4000 6000 8000 10000 # labeled examples 12000 14000 16000

% error 10 5 4

rst reached random active 3,500 1,500 9,000 2,750 13,000 3,500

% label savings 57 69 73

Fundamental Perspectives
game theory loss minimization an information-geometric view

Fundamental Perspectives
game theory loss minimization an information-geometric view

Just a Game

[with Freund]

can view boosting as a game, a formal interaction between

booster and weak learner
on each round t:

booster chooses distribution Dt weak learner responds with weak classier ht

game theory: studies interactions between all sorts of

players

Games

game dened by matrix M:

Rock Paper Scissors

Rock 1/2 0 1

Paper 1 1/2 0

Scissors 0 1 1/2

row player (Mindy) chooses row i column player (Max) chooses column j (simultaneously) Mindys goal: minimize her loss M(i, j) assume (wlog) all entries in [0, 1]

Randomized Play
usually allow randomized play:

Mindy chooses distribution P over rows Max chooses distribution Q over columns (simultaneously)

Mindys (expected) loss

=
i,j

P(i)M(i, j)Q(j)

= P MQ M(P, Q)

i, j = pure strategies P, Q = mixed strategies m = # rows of M also write M(i, Q) and M(P, j) when one side plays pure and

other plays mixed

Sequential Play
say Mindy plays before Max if Mindy chooses P then Max will pick Q to maximize

M(P, Q) loss will be L(P) max M(P, Q)
Q

so Mindy should pick P to minimize L(P)

loss will be min L(P) = min max M(P, Q)
P P Q

similarly, if Max plays rst, loss will be

max min M(P, Q)
Q P

Minmax Theorem
playing second (with knowledge of other players move)

cannot be worse than playing rst, so: min max M(P, Q) max min M(P, Q)
P Q Q P

Mindy plays rst

Mindy plays second

von Neumanns minmax theorem:

min max M(P, Q) = max min M(P, Q)
P Q Q P

in words: no advantage to playing second

Optimal Play
minmax theorem:

min max M(P, Q) = max min M(P, Q) = value v of game
P Q Q P

optimal strategies:

P = arg minP maxQ M(P, Q) = minmax strategy Q = arg maxQ minP M(P, Q) = maxmin strategy

in words:

Mindys minmax strategy P guarantees loss v (regardless of Maxs play) optimal because Max has maxmin strategy Q that can force loss v (regardless of Mindys play)

e.g.: in RPS, P = Q = uniform solving game = nding minmax/maxmin strategies

Weaknesses of Classical Theory
seems to fully answer how to play games just compute

minmax strategy (e.g., using linear programming)
weaknesses:

game M may be unknown game M may be extremely large opponent may not be fully adversarial may be possible to do better than value v e.g.: Lisa (thinks): Poor predictable Bart, always takes Rock. Bart (thinks): Good old Rock, nothing beats that.

Repeated Play

if only playing once, hopeless to overcome ignorance of game

M or opponent
but if game played repeatedly, may be possible to learn to

play well
goal: play (almost) as well as if knew game and how

opponent would play ahead of time

Repeated Play (cont.)
M unknown for t = 1, . . . , T :

Mindy chooses Pt Max chooses Qt (possibly depending on Pt ) Mindys loss = M(Pt , Qt ) Mindy observes loss M(i, Qt ) of each pure strategy i

want:

1 T

T

M(Pt , Qt ) min
t=1 P

1 T

T

M(P, Qt ) + [small amount]
t=1

actual average loss

best loss (in hindsight)

Multiplicative-Weights Algorithm (MW)
choose > 0 initialize: P1 = uniform on round t:

[with Freund]

Pt+1 (i) =

Pt (i) exp ( M(i, Qt )) normalization

idea: decrease weight of strategies suering the most loss directly generalizes [Littlestone & Warmuth] other algorithms: [Hannan57] [Blackwell56] [Foster & Vohra] [Fudenberg & Levine]

. . .

Analysis
Theorem: can choose so that, for any game M with m

rows, and any opponent, 1 T
T

M(Pt , Qt )
t=1

1 min P T

T

M(P, Qt ) + T
t=1

actual average loss where T = O
regret T is:

best average loss ( v ) 0

ln m T

logarithmic in # rows m independent of # columns

therefore, can use when working with very large games

Solving a Game
suppose game M played repeatedly

[with Freund]

Mindy plays using MW on round t, Max chooses best response: Qt = arg max M(Pt , Q)
Q

let

1 P= T

T

Pt ,
t=1

1 Q= T

T

Qt
t=1

can prove that P and Q are T -approximate minmax and

maxmin strategies: max M(P, Q) v + T
Q

and min M(P, Q) v T
P

Boosting as a Game

Mindy (row player) booster Max (column player) weak learner matrix M:

row training example column weak classier M(i, j) = 1 if j-th weak classier correct on i-th training example 0 else encodes which weak classiers correct on which examples huge # of columns one for every possible weak classier

Boosting and the Minmax Theorem

-weak learning assumption:

for every distribution on examples can nd weak classier with weighted error

1 2

equivalent to:

(value of game M)

1 2

+

by minmax theorem, implies that:

some weighted majority classier that correctly classies all training examples with margin 2 further, weights are given by maxmin strategy of game M

Idea for Boosting

maxmin strategy of M has perfect (training) accuracy and

large margins
nd approximately using earlier algorithm for solving a game

i.e., apply MW to M

yields (variant of) AdaBoost

AdaBoost and Game Theory
summarizing:

weak learning assumption implies maxmin strategy for M denes large-margin classier AdaBoost nds maxmin strategy by applying general algorithm for solving games through repeated play

consequences:

weights on weak classiers converge to (approximately) maxmin strategy for game M (average) of distributions Dt converges to (approximately) minmax strategy margins and edges connected via minmax theorem explains why AdaBoost maximizes margins

dierent instantiation of game-playing algorithm gives online

learning algorithms (such as weighted majority algorithm)

Fundamental Perspectives
game theory loss minimization an information-geometric view

AdaBoost and Loss Minimization
many (most?) learning and statistical methods can be viewed

as minimizing loss (a.k.a. cost or objective) function measuring t to data: 2 e.g. least squares regression i (F (xi ) yi )
AdaBoost also minimizes a loss function helpful to understand because:

claries goal of algorithm and useful in proving convergence properties decoupling of algorithm from its objective means: faster algorithms possible for same objective same algorithm may generalize for new learning challenges

What AdaBoost Minimizes

recall proof of training error bound:

training error(Hnal )
t

Zt

Zt = t e t + (1 t )e t = 2 t (1 t ) t chosen to minimize Zt ht chosen to minimize t same as minimizing Zt (since increasing in t on [0, 1/2]) equivalent to greedily minimizing
t

closer look:

so: both AdaBoost and weak learner minimize Zt on round t

Zt

AdaBoost and Exponential Loss
so AdaBoost is greedy procedure for minimizing

exponential loss Zt =
t

1 m

exp(yi F (xi ))
i

where F (x) =
t

t ht (x)

why exponential loss?

intuitively, strongly favors F (xi ) to have same sign as yi upper bound on training error smooth and convex (but very loose)

how does AdaBoost minimize it?

Coordinate Descent
{g1 , . . . , gN } = space of all weak classiers
N

[Breiman]

then can write F (x) =
t

t ht (x) =
j=1

j gj (x)

want to nd 1 , . . . , N to minimize

L(1 , . . . , N ) =
i

AdaBoost is actually doing coordinate descent on this

exp yi

j

j gj (xi )

optimization problem: initially, all j = 0 each round: choose one coordinate j (corresponding to ht ) and update (increment by t ) choose update causing biggest decrease in loss powerful technique for minimizing over huge space of functions

Functional Gradient Descent
want to minimize

[Mason et al.][Friedman]

L(F ) = L(F (x1 ), . . . , F (xm )) =
i

exp(yi F (xi ))

say have current estimate F and want to improve to do gradient descent, would like update

F F F L(F )
but update restricted in class of weak classiers

F F + ht
so choose ht closest to F L(F ) equivalent to AdaBoost

Estimating Conditional Probabilities

[Friedman, Hastie & Tibshirani]

often want to estimate probability that y = +1 given x AdaBoost minimizes (empirical version of):

Ex,y e yF (x) = Ex Pr [y = +1|x] e F (x) + Pr [y = 1|x] e F (x) where x, y random from true distribution
over all F , minimized when

F (x) = or

1 ln 2

Pr [y = +1|x] Pr [y = 1|x] 1 1 + e 2F (x)

Pr [y = +1|x] =

so, to convert F output by AdaBoost to probability estimate,

use same formula

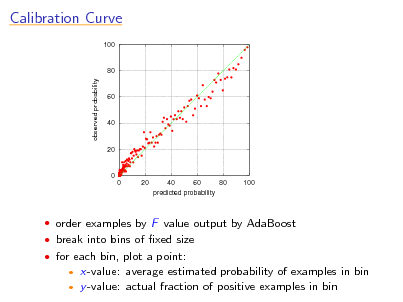
Calibration Curve
100

80
observed probability

60

40

20

0 0 20 40 60 80 100 predicted probability

order examples by F value output by AdaBoost break into bins of xed size for each bin, plot a point:

x-value: average estimated probability of examples in bin y -value: actual fraction of positive examples in bin

A Synthetic Example
x [2, +2] uniform Pr [y = +1|x] = 2x
2

m = 500 training examples
1 1

0.5

0.5

0 -2 -1 0 1 2

0 -2 -1 0 1 2

if run AdaBoost with stumps and convert to probabilities,

result is poor extreme overtting

Regularization
AdaBoost minimizes

L() =
i

to avoid overtting, want to constrain to make solution

exp yi

j

j gj (xi )

smoother
(1 ) regularization:

minimize: L() subject to:
or:
1

B

minimize: L() +
other norms possible

1

1 (lasso) currently popular since encourages sparsity
[Tibshirani]

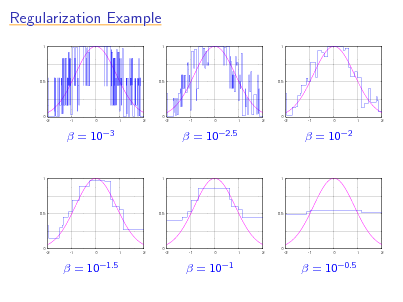
Regularization Example
1 1 1

0.5

0.5

0.5

0 -2 -1 0 1 2

0 -2 -1 0 1 2

0 -2 -1 0 1 2

=

103

=

102.5

=

102

1

1

1

0.5

0.5

0.5

0 -2 -1 0 1 2

0 -2 -1 0 1 2

0 -2 -1 0 1 2

=

101.5

=

101

=

100.5

Regularization and AdaBoost
0.6 individual classifier weights 0.4 0.2 0 -0.2 -0.4 -0.6 0 0.5 1 1.5 2 2.5

[Hastie, Tibshirani & Friedman; Rosset, Zhu & Hastie]
0.6 individual classifier weights 0.4 0.2 0 -0.2 -0.4 -0.6 0 0.5 1 1.5 2 2.5

B Experiment 1: regularized

T Experiment 2: AdaBoost run

solution vectors plotted as function of B

with t xed to (small) solution vectors plotted as function of T

plots are identical! can prove under certain (but not all) conditions that results will be the same (as 0) [Zhao & Yu]

Regularization and AdaBoost

suggests stopping AdaBoost early is akin to applying

1 -regularization
caveats:

does not strictly apply to AdaBoost (only variant) not helpful when boosting run to convergence (would correspond to very weak regularization)

in fact, in limit of vanishingly weak regularization (B ),

solution converges to maximum margin solution
[Rosset, Zhu & Hastie]

Benets of Loss-Minimization View

immediate generalization to other loss functions and learning

problems

e.g. squared error for regression e.g. logistic regression (by only changing one line of AdaBoost)

sensible approach for converting output of boosting into

conditional probability estimates
helpful connection to regularization basis for proving AdaBoost is statistically consistent

i.e., under right assumptions, converges to best possible classier [Bartlett & Traskin]

A Note of Caution

tempting (but incorrect!) to conclude:

AdaBoost is just an algorithm for minimizing exponential loss AdaBoost works only because of its loss function more powerful optimization techniques for same loss should work even better

incorrect because:

other algorithms that minimize exponential loss can give very poor generalization performance compared to AdaBoost

for example...

An Experiment
data:

instances x uniform from {1, +1}10,000 label y = majority vote of three coordinates weak classier = single coordinate (or its negation) training set size m = 1000 algorithms (all provably minimize exponential loss): standard AdaBoost gradient descent on exponential loss AdaBoost, but in which weak classiers chosen at random results:

exp. loss 1010 1020 1040 10100

stand. AdaB. 0.0 [94] 0.0 [190] 0.0 [382] 0.0 [956]

% test error [# rounds] grad. desc. random AdaB. 40.7 [5] 44.0 [24,464] 40.8 [9] 41.6 [47,534] 40.8 [21] 40.9 [94,479] 40.8 [70] 40.3 [234,654]

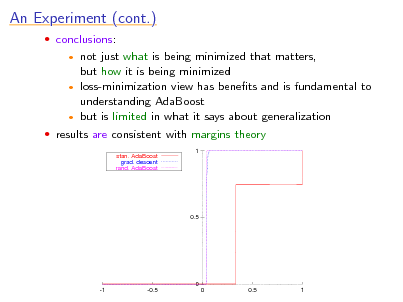
An Experiment (cont.)
conclusions:

not just what is being minimized that matters, but how it is being minimized loss-minimization view has benets and is fundamental to understanding AdaBoost but is limited in what it says about generalization results are consistent with margins theory

stan. AdaBoost grad. descent rand. AdaBoost 1

0.5

0 -1 -0.5 0 0.5 1

Fundamental Perspectives
game theory loss minimization an information-geometric view

A Dual Information-Geometric Perspective

loss minimization focuses on function computed by AdaBoost

(i.e., weights on weak classiers)
dual view: instead focus on distributions Dt

(i.e., weights on examples)
dual perspective combines geometry and information theory exposes underlying mathematical structure basis for proving convergence

An Iterative-Projection Algorithm
say want to nd point closest to x0 in set

P = { intersection of N hyperplanes }
algorithm:

[Bregman; Censor & Zenios]

start at x0 repeat: pick a hyperplane and project onto it

P x0

if P = , under general conditions, will converge correctly

AdaBoost is an Iterative-Projection Algorithm
points = distributions Dt over training examples distance = relative entropy:

[Kivinen & Warmuth]

RE (P

Q) =
i

P(i) ln

P(i) Q(i)

reference point x0 = uniform distribution hyperplanes dened by all possible weak classiers gj :

D(i)yi gj (xi ) = 0 Pr [gj (xi ) = yi ] =
i iD

1 2

intuition: looking for hardest distribution

AdaBoost as Iterative Projection (cont.)

algorithm:

start at D1 = uniform for t = 1, 2, . . .: pick hyperplane/weak classier ht gj Dt+1 = (entropy) projection of Dt onto hyperplane = arg min RE (D Dt )
D:
i

D(i)yi gj (xi )=0

claim: equivalent to AdaBoost further: choosing ht with minimum error choosing farthest

hyperplane

Boosting as Maximum Entropy
corresponding optimization problem:
DP

min RE (D

uniform) max entropy(D)
DP

where

P = feasible set = D:
i

D(i)yi gj (xi ) = 0 j

P = weak learning assumption does not hold

in this case, Dt (unique) solution

if weak learning assumption does hold then

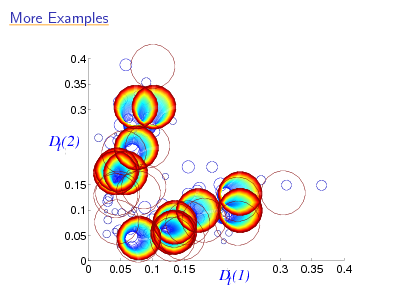
P= Dt can never converge dynamics are fascinating but unclear in this case

Visualizing Dynamics
plot one circle for each round t:

[with Rudin & Daubechies]

center at (Dt (1), Dt (2)) radius t (color also varies with t)
t=3
0.5

11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000

0.4

t=6
11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000

d

D (2) t
t,2

t=1 t=4 t=5
0.2
111111 000000 0.3 d 111111 000000 0.4 111111 000000 t,1 111111 000000 111111 000000 111111 000000 111111 000000

t=2

0.2

D (1) t

0.5

in all cases examined, appears to converge eventually to cycle

open if always true

More Examples
0.35

0.25
111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000

D (2) t

dt,2

0.1

0 0

111111 0.1 000000 111111 000000 d 111111 000000 111111 000000 111111 000000

111111 000000 111111 000000

D (1) t t,1

0.2

0.3

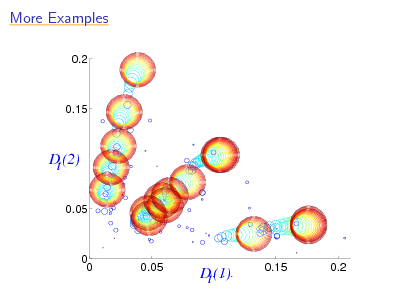
More Examples
0.2

0.15
111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000

d

D (2) t

0.05

t,12

0 0

0.05

d (1) D t,11 t

11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000

0.15

0.2

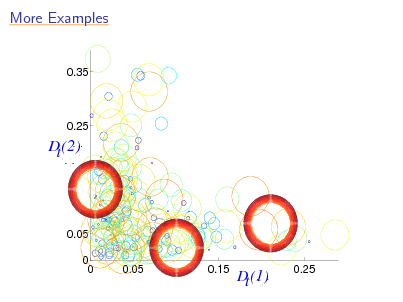
More Examples

0.35

111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000 111111 000000

0.25

d

D (2) t

0.05 0 0 0.05 0.15
11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000

t,2

Ddt,1 t (1)

0.25

More Examples
0.4 0.35 0.3
11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000 11111 00000

d

D (2) t

0.15 0.1 0.05 0 0 0.05 0.1 0.15
11111 00000 11111 00000 11111 00000 11111 00000 t,1 11111 00000 11111 00000

t,2

d D (1) t

0.3

0.35

0.4

Unifying the Two Cases
two distinct cases:

[with Collins & Singer]

weak learning assumption holds P = dynamics unclear weak learning assumption does not hold P = can prove convergence of Dt s to unify: work instead with unnormalized versions of Dt s Dt (i) exp(t yi ht (xi )) standard AdaBoost: Dt+1 (i) = normalization instead: dt+1 (i) = dt (i) exp(t yi ht (xi )) dt+1 (i) Dt+1 (i) = normalization

algorithm is unchanged

Reformulating AdaBoost as Iterative Projection
points = nonnegative vectors dt distance = unnormalized relative entropy:

RE (p

q) =
i

p(i) ln

p(i) q(i)

+ q(i) p(i)

reference point x0 = 1 (all 1s vector) hyperplanes dened by weak classiers gj :

d(i)yi gj (xi ) = 0
i

resulting iterative-projection algorithm is again equivalent to

AdaBoost

Reformulated Optimization Problem

optimization problem:

min RE (d
dP

1)

where

P=

d:
i

d(i)yi gj (xi ) = 0 j

note: feasible set P never empty (since 0 P)

Exponential Loss as Entropy Optimization
all vectors dt created by AdaBoost have form:

d(i) = exp yi

j

j gj (xi )

let Q = { all vectors d of this form } can rewrite exponential loss:

inf
i

exp yi

j

j gj (xi )

=

dQ

inf

d(i)
i

= min
dQ dQ i

d(i) d)

= min RE (0
Q = closure of Q

Duality

[Della Pietra, Della Pietra & Laerty]

presented two optimization problems:

min RE (d
dP

1) d)

min RE (0
dQ

which is AdaBoost solving? Both! problems have same solution moreover: solution given by unique point in P Q problems are convex duals of each other

Convergence of AdaBoost
can use to prove AdaBoost converges to common solution of

both problems: can argue that d = lim dt is in P vectors dt are in Q always d Q d P Q d solves both optimization problems
so:

AdaBoost minimizes exponential loss exactly characterizes limit of unnormalized distributions likewise for normalized distributions when weak learning assumption does not hold

also, provides additional link to logistic regression

only need slight change in optimization problem
[with Collins & Singer; Lebannon & Laerty]

Practical Extensions
multiclass classication ranking problems condence-rated predictions

Practical Extensions
multiclass classication ranking problems condence-rated predictions

Multiclass Problems
say y Y where |Y | = k direct approach (AdaBoost.M1):

[with Freund]

ht : X Y Dt+1 (i) = Dt (i) Zt e t e t
y Y

if yi = ht (xi ) if yi = ht (xi ) t
t:ht (x)=y

Hnal (x) = arg max

can prove same bound on error if t : t 1/2

in practice, not usually a problem for strong weak learners (e.g., C4.5) signicant problem for weak weak learners (e.g., decision stumps) instead, reduce to binary

The One-Against-All Approach
break k-class problem into k binary problems and

solve each separately
say possible labels are Y = { , , , }

x1 x2 x3 x4 x5

x1 x2 x3 x4 x5

+

x1 x2 x3 x4 x5

+ +

x1 x2 x3 x4 x5

+

x1 x2 x3 x4 x5

+

to classify new example, choose label predicted to be most

positive
AdaBoost.MH problem: not robust to errors in predictions [with Singer]

Using Output Codes

[with Allwein & Singer][Dietterich & Bakiri]

M
reduce to binary using

coding matrix M
rows of M code words

1 + + + 4 + + +

2 + + x1 x2 x3 x4 x5

3 + + + 5 + + +

4 + +

5 + +

1 x1 x2 x3 x4 x5 x1 x2 x3 x4 x5 + + + x1 x2 x3 x4 x5

2 + + x1 x2 x3 x4 x5

3 + + + + x1 x2 x3 x4 x5

to classify new example, choose closest row of M

Output Codes (continued)

if rows of M far from one another,

will be highly robust to errors
potentially much faster when k (# of classes) large disadvantage:

binary problems may be unnatural and hard to solve

Practical Extensions
multiclass classication ranking problems condence-rated predictions

Ranking Problems

[with Freund, Iyer & Singer]

goal: learn to rank objects (e.g., movies, webpages, etc.) from

examples
can reduce to multiple binary questions of form:

is or is not object A preferred to object B?
now apply (binary) AdaBoost RankBoost

Application: Finding Cancer Genes

[Agarwal & Sengupta]

examples are genes (described by microarray vectors) want to rank genes from most to least relevant to leukemia data sizes:

7129 genes total 10 known relevant 157 known irrelevant

Top-Ranked Cancer Genes
Gene 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. KIAA0220 G-gamma globin Delta-globin Brain-expressed HHCPA78 homolog Myeloperoxidase Probable protein disulde isomerase ER-60 precursor NPM1 Nucleophosmin CD34 Elongation factor-1-beta CD24 Relevance Summary

= = = = =

known therapeutic target potential therapeutic target known marker potential marker no link found

Practical Extensions
multiclass classication ranking problems condence-rated predictions

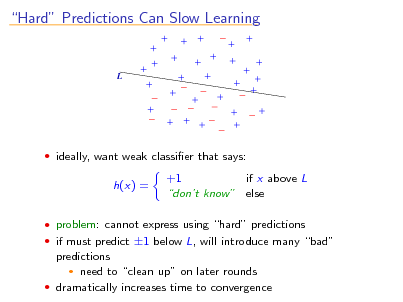
Hard Predictions Can Slow Learning

L

ideally, want weak classier that says:

h(x) =

+1 if x above L dont know else

problem: cannot express using hard predictions if must predict 1 below L, will introduce many bad

predictions need to clean up on later rounds dramatically increases time to convergence

Condence-Rated Predictions

[with Singer]

useful to allow weak classiers to assign condences to

predictions
formally, allow ht : X R

sign(ht (x)) = prediction |ht (x)| = condence

use identical update:

Dt+1 (i) =

Dt (i) exp(t yi ht (xi )) Zt

and identical rule for combining weak classiers
question: how to choose t and ht on each round

Condence-Rated Predictions (cont.)
saw earlier:

training error(Hnal )
t

Zt =

1 m

exp yi
i t

t ht (xi )

therefore, on each round t, should choose t ht to minimize:

Zt =
i

Dt (i) exp(t yi ht (xi ))

in many cases (e.g., decision stumps), best condence-rated

weak classier has simple form that can be found eciently

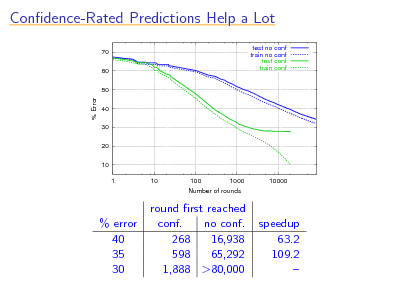
Condence-Rated Predictions Help a Lot
70 60 50 test no conf train no conf test conf train conf

% Error

40 30 20 10 1 10 100 1000 Number of rounds 10000

% error 40 35 30

round rst reached conf. no conf. 268 16,938 598 65,292 1,888 >80,000

speedup 63.2 109.2

Application: Boosting for Text Categorization

[with Singer]

weak classiers: very simple weak classiers that test on

simple patterns, namely, (sparse) n-grams nd parameter t and rule ht of given form which minimize Zt use eciently implemented exhaustive search
How may I help you data:

7844 training examples 1000 test examples categories: AreaCode, AttService, BillingCredit, CallingCard, Collect, Competitor, DialForMe, Directory, HowToDial, PersonToPerson, Rate, ThirdNumber, Time, TimeCharge, Other.

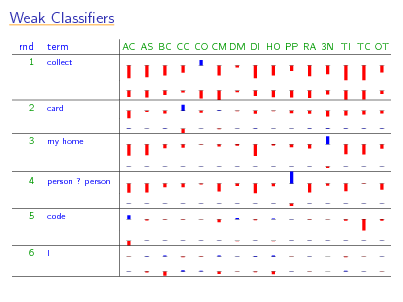
Weak Classiers
rnd
1

term
collect

AC AS BC CC CO CM DM DI HO PP RA 3N TI TC OT

2

card

3

my home

4

person ? person

5

code

6

I

More Weak Classiers
rnd
7

term
time

AC AS BC CC CO CM DM DI HO PP RA 3N TI TC OT

8

wrong number

9 10 11

how call seven

12

trying to

13

and

More Weak Classiers
rnd
14

term
third

AC AS BC CC CO CM DM DI HO PP RA 3N TI TC OT

15 16

to for

17

charges

18

dial

19

just

Finding Outliers
examples with most weight are often outliers (mislabeled and/or ambiguous)
Im trying to make a credit card call (Collect) hello (Rate) yes Id like to make a long distance collect call please (CallingCard) calling card please (Collect) yeah Id like to use my calling card number (Collect) can I get a collect call (CallingCard) yes I would like to make a long distant telephone call and have the charges billed to another number (CallingCard DialForMe) yeah I can not stand it this morning I did oversea (BillingCredit) call is so bad yeah special offers going on for long distance (AttService Rate) mister allen please william allen (PersonToPerson) yes maam I Im trying to make a long distance call to a non dialable point in san miguel philippines (AttService Other)

Advanced Topics
optimal accuracy optimal eciency boosting in continuous time

Advanced Topics
optimal accuracy optimal eciency boosting in continuous time

Optimal Accuracy
noise or uncertainty

[Bartlett & Traskin]

usually, impossible to get perfect accuracy due to intrinsic Bayes optimal error = best possible error of any classier

usually > 0

can prove AdaBoosts classier converges to Bayes optimal if:

enough data run for many (but not too many) rounds weak classiers suciently rich

universally consistent related results: [Jiang], [Lugosi & Vayatis], [Zhang & Yu], . . . means:

AdaBoost can (theoretically) learn optimally even in noisy settings but: does not explain why works when run for very many rounds

Boosting and Noise

[Long & Servedio]

can construct data source on which AdaBoost fails miserably

with even tiny amount of noise (say, 1%) Bayes optimal error = 1% (obtainable by classier of same form as AdaBoost) AdaBoost provably has error 50%
holds even if:

given unlimited training data use any method for minimizing exponential loss

also holds:

for most other convex losses even if add regularization e.g. applies to SVMs, logistic regression, . . .

Boosting and Noise (cont.)

shows:

consistency result can fail badly if weak classiers not rich enough AdaBoost (and lots of other loss-based methods) susceptible to noise regularization might not help

how to handle noise?

on real-world datasets, AdaBoost often works anyway various theoretical algorithms based on branching programs (e.g., [Kalai & Servedio], [Long & Servedio])

Advanced Topics
optimal accuracy optimal eciency boosting in continuous time

Optimal Eciency
for AdaBoost, saw: training error e 2
2T

[Freund]

is AdaBoost most ecient boosting algorithm?

no!
given T rounds and -weak learning assumption,

boost-by-majority (BBM) algorithm is provably exactly best possible:
T /2

training error
j=0

T j

1 2

+

j

1 2

T j

(probability of T /2 heads in T coin ips if probability of heads = 1 + ) 2
AdaBoosts training error is like Cherno approximation of

BBMs

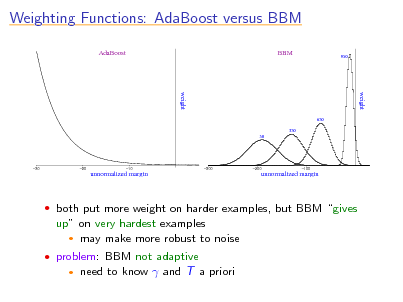
Weighting Functions: AdaBoost versus BBM
AdaBoost BBM
950

weight
650 350 50

weight

30

20

unnormalized margin

s

10

300

200

unnormalized margin

s

100

both put more weight on harder examples, but BBM gives

up on very hardest examples may make more robust to noise
problem: BBM not adaptive

need to know and T a priori

Advanced Topics
optimal accuracy optimal eciency boosting in continuous time

Boosting in Continuous Time

[Freund]

idea: let get very small so that -weak learning assumption

eventually satised
need to make T correspondingly large if scale time to begin at = 0 and end at = 1, then each

boosting round takes time 1/T
in limit T , boosting is happening in continuous time

BrownBoost
algorithm has sensible limit called BrownBoost

(due to connection to Brownian motion)
harder to implement, but potentially more resistant to noise

and outliers, e.g.: dataset letter noise 0% 10% 20% 0% 10% 20% AdaBoost 3.7 10.8 15.7 4.9 12.1 21.3 BrownBoost 4.2 7.0 10.5 5.2 6.2 7.4

satimage

[Cheamanunkul, Ettinger & Freund]

Conclusions
from dierent perspectives, AdaBoost can be interpreted as:

a method for boosting the accuracy of a weak learner a procedure for maximizing margins an algorithm for playing repeated games a numerical method for minimizing exponential loss an iterative-projection algorithm based on an information-theoretic geometry

none is entirely satisfactory by itself, but each useful in its

own way
taken together, create rich theoretical understanding

connect boosting to other learning problems and techniques provide foundation for versatile set of methods with many extensions, variations and applications

References

Robert E. Schapire and Yoav Freund.

Boosting: Foundations and Algorithms. MIT Press, 2012.