Probabilistic Topic Models
David M. Blei
Department of Computer Science Princeton University
September 2, 2012
Probabilistic topic modeling provides a suite of tools for the unsupervised analysis of large collections of documents. Topic modeling algorithms can uncover the underlying themes of a collection and decompose its documents according to those themes. This analysis can be used for corpus exploration, document search, and a variety of prediction problems. My lectures will describe three aspects of topic modeling: Topic modeling assumptions Algorithms for computing with topic models Applications of topic models In (1), I will describe latent Dirichlet allocation (LDA), which is one of the simplest topic models, and then describe a variety of ways that we can build on it. These include dynamic topic models, correlated topic models, supervised topic models, author-topic models, bursty topic models, Bayesian nonparametric topic models, and others. I will also discuss some of the fundamental statistical ideas that are used in building topic models, such as distributions on the simplex, hierarchical Bayesian modeling, and models of mixed-membership. In (2), I will review how we compute with topic models. I will describe approximate posterior inference for directed graphical models using both sampling and variational inference, and I will discuss the practical issues and pitfalls in developing these algorithms for topic models. Finally, I will describe some of our most recent work on building algorithms that can scale to millions of documents and documents arriving in a stream. In (3), I will discuss applications of topic models. These include applications to images, music, social networks, and other data in which we hope to uncover hidden patterns. I will describe some of our recent work on adapting topic modeling algorithms to collaborative filtering, legislative modeling, and bibliometrics without citations. Finally, I will discuss some future directions and open research problems in topic models.
Scroll with j/k | | | Size

Probabilistic Topic Models
David M. Blei
Department of Computer Science Princeton University
September 2, 2012
1

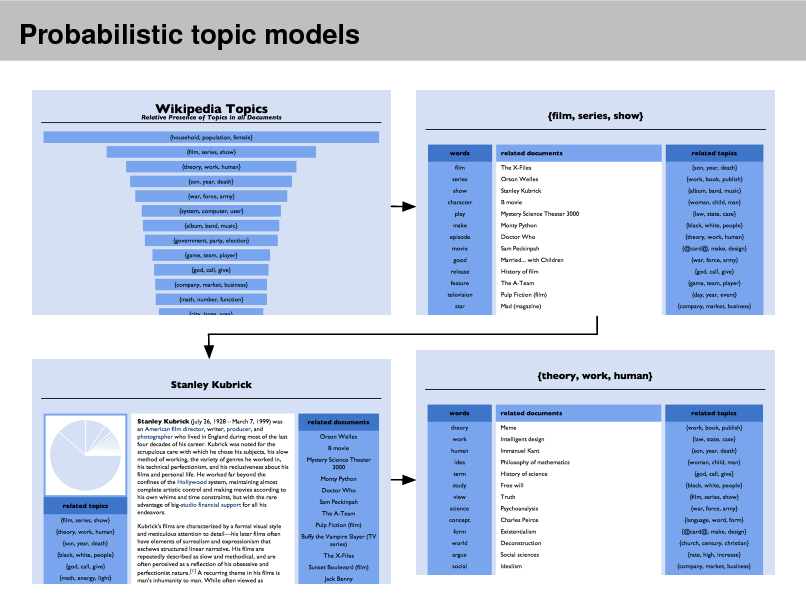
Probabilistic topic models
As more information becomes available, it becomes more difcult to nd and discover what we need.
We need new tools to help us organize, search, and understand these vast amounts of information.
2

Probabilistic topic models
Topic modeling provides methods for automatically organizing, understanding, searching, and summarizing large electronic archives.
1 2 3
Discover the hidden themes that pervade the collection. Annotate the documents according to those themes. Use annotations to organize, summarize, search, form predictions.
3

Probabilistic topic models
Genetics human genome dna genetic genes sequence gene molecular sequencing map information genetics mapping project sequences Evolution Disease evolution disease evolutionary host species bacteria organisms diseases life resistance origin bacterial biology new groups strains phylogenetic control living infectious diversity malaria group parasite new parasites two united common tuberculosis Computers computer models information data computers system network systems model parallel methods networks software new simulations
4
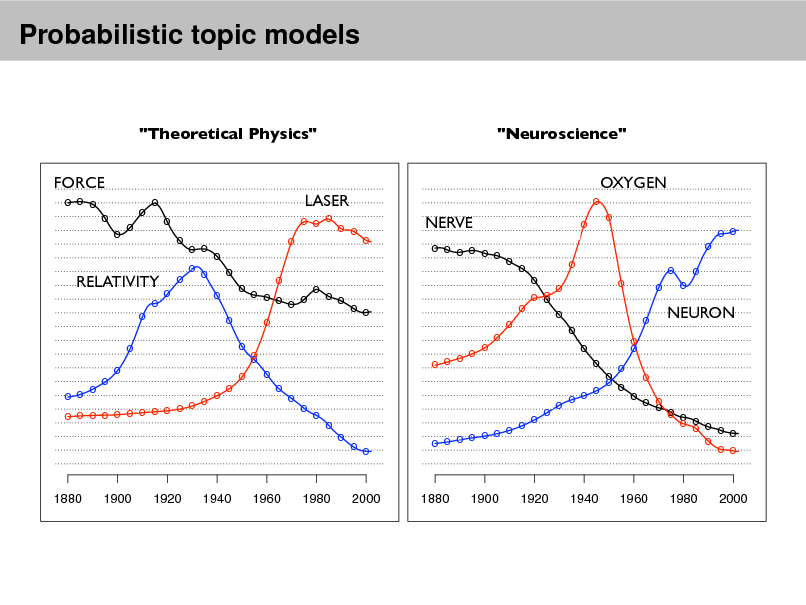
Probabilistic topic models
"Theoretical Physics" FORCE
o o o o o o o o o o o
"Neuroscience" OXYGEN
o
LASER
o o o o o
NERVE
o o o o o o o o o o
o
o o o o o o o o o o
o o o o o o o o RELATIVITY o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o
o o o o o o o
o o o o o o o o o o o o o o
NEURON
o o o o o o o o o o o o o o o o o o o o o o
o
o
o o
o o o o o o o o o
o
1880
1900
1920
1940
1960
1980
2000
1880
1900
1920
1940
1960
1980
2000
5
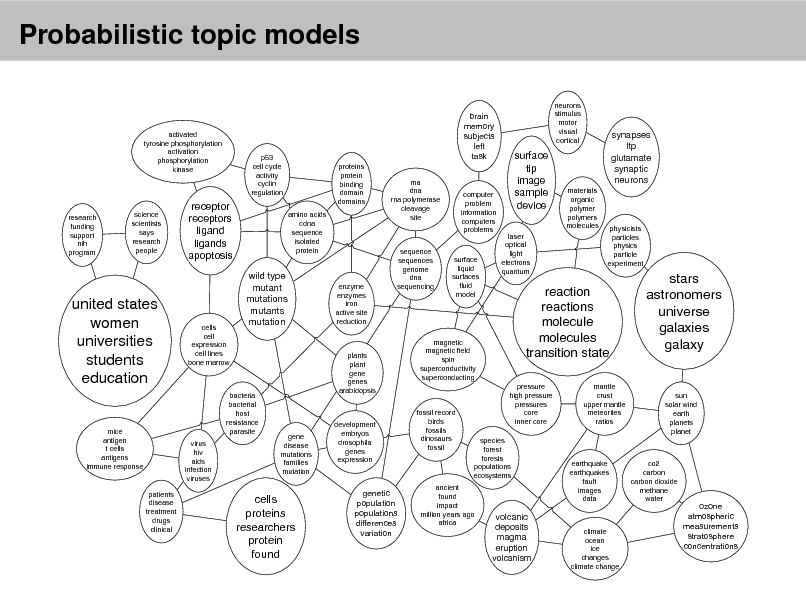
Probabilistic topic models
brain memory subjects left task
proteins protein binding domain domains amino acids cdna sequence isolated protein rna dna rna polymerase cleavage site neurons stimulus motor visual cortical
activated tyrosine phosphorylation activation phosphorylation kinase
p53 cell cycle activity cyclin regulation
research funding support nih program
science scientists says research people
receptor receptors ligand ligands apoptosis
wild type mutant mutations mutants mutation
computer problem information computers problems
surface tip image sample device
laser optical light electrons quantum
synapses ltp glutamate synaptic neurons
materials organic polymer polymers molecules
united states women universities students education
cells cell expression cell lines bone marrow
enzyme enzymes iron active site reduction
sequence sequences genome dna sequencing
surface liquid surfaces uid model
physicists particles physics particle experiment
mice antigen t cells antigens immune response
bacteria bacterial host resistance parasite virus hiv aids infection viruses patients disease treatment drugs clinical
plants plant gene genes arabidopsis
magnetic magnetic eld spin superconductivity superconducting
reaction reactions molecule molecules transition state
pressure high pressure pressures core inner core mantle crust upper mantle meteorites ratios
stars astronomers universe galaxies galaxy
gene disease mutations families mutation
development embryos drosophila genes expression
fossil record birds fossils dinosaurs fossil
sun solar wind earth planets planet
species forest forests populations ecosystems
cells proteins researchers protein found
genetic population populations differences variation
ancient found impact million years ago africa
earthquake earthquakes fault images data
co2 carbon carbon dioxide methane water
volcanic deposits magma eruption volcanism
climate ocean ice changes climate change
ozone atmospheric measurements stratosphere concentrations
6
Probabilistic topic models
Quantum lower bounds by polynomials On the power of bounded concurrency I: finite automata Dense quantum coding and quantum finite automata Classical physics and the Church--Turing Thesis
quantum automata nc automaton languages
online scheduling task competitive tasks
approximation s points distance convex routing adaptive network networks protocols
Nearly optimal algorithms and bounds for multilayer channel routing How bad is selfish routing? Authoritative sources in a hyperlinked environment Balanced sequences and optimal routing
machine domain degree degrees polynomials
n functions polynomial log algorithm
networks protocol network packets link
An optimal algorithm for intersecting line segments in the plane Recontamination does not help to search a graph A new approach to the maximum-flow problem The time complexity of maximum matching by simulated annealing
graph graphs edge minimum vertices
learning learnable statistical examples classes
the,of a, is and
n algorithm time log bound logic programs systems language sets
m merging networks sorting multiplication
database constraints algebra boolean relational
constraint dependencies local consistency tractable
Module algebra On XML integrity constraints in the presence of DTDs Closure properties of constraints Dynamic functional dependencies and database aging
logic logics query theories languages
consensus objects messages protocol asynchronous
system systems performance analysis distributed
learning knowledge reasoning verication circuit
trees regular tree search compression
Magic Functions: In Memoriam: Bernard M. Dwork 1923--1998 A mechanical proof of the Church-Rosser theorem Timed regular expressions On the power and limitations of strictness analysis
proof property program resolution abstract
formulas rstorder decision temporal queries
database transactions retrieval concurrency restrictions
networks queuing asymptotic productform server
Single-class bounds of multi-class queuing networks The maximum concurrent flow problem Contention in shared memory algorithms Linear probing with a nonuniform address distribution
7

Probabilistic topic models
predicted caption: birds nest leaves branch tree
tain people
Automatic image annotation predicted caption: caption: Automatic predictedwaterpattern textile display predicted caption: tree image annotation leaves branch sky people market tree mountain people birds nest
p p
predicted caption: predicted caption: predicted caption: p predicted caption: predicted predicted caption: utomatic image mountainnest caption: flowers tree coralpredicted caption: image anno SCOTLAND WATER people marketWATER BUILDING e coral SKY WATER TREE sky water buildings people fish branch Automatic sky water textile display SKY patternbuildings people mountain s sky water tree mountain people annotation hills tree birds scotland water ocean leaves water tree predicted caption: MOUNTAIN PEOPLE sky water tree mountain people predicted caption:HILLS TREEpredicted caption: FLOWER PEOPLE WATER birds nest leaves branch tree people market pattern textile display
predicted caption: predicted caption: predicted caption: fish water ocean tree coral sky water buildings people mountain scotland water flowers hills tree Probabilistic modelsof text and images p.5/53 predicted predicted caption: predicted caption: caption: predicted caption: caption: predicted caption: predicted caption: predicted FISH WATERtree coral MARKET PATTERN tain peoplefish water ocean leaves branch treePEOPLE sky water pattern textile display water flowersleavestree sky water buildings peoplemountain people birds nest OCEAN people market tree mountain scotland BIRDS NEST TREE birds nest hills branch tree
pr pe
TREE CORAL
TEXTILE DISPLAY
BRANCH LEAVES
8
![Slide: Probabilistic topic models
Derek E. Wildman et al., Implications of Natural Selection in Shaping 99.4% Nonsynonymous DNA Identity between Humans and Chimpanzees: Enlarging Genus Homo, PNAS (2003) [178 citations]
0.030
0.025
Jared M. Diamond, Distributional Ecology of New Guinea Birds. Science (1973) [296 citations]
WeightedInfluence
0.020
0.015
William K. Gregory, The New Anthropogeny: Twenty-Five Stages of Vertebrate Evolution, from Silurian Chordate to Man, Science (1933) [3 citations]
0.010
0.005
0.000 1880 1900 1920 1940 1960 1980 2000
Year W. B. Scott, The Isthmus of Panama in Its Relation to the Animal Life of North and South America, Science (1916) [3 citations]](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_009.png)
Probabilistic topic models
Derek E. Wildman et al., Implications of Natural Selection in Shaping 99.4% Nonsynonymous DNA Identity between Humans and Chimpanzees: Enlarging Genus Homo, PNAS (2003) [178 citations]
0.030
0.025
Jared M. Diamond, Distributional Ecology of New Guinea Birds. Science (1973) [296 citations]
WeightedInfluence
0.020
0.015
William K. Gregory, The New Anthropogeny: Twenty-Five Stages of Vertebrate Evolution, from Silurian Chordate to Man, Science (1933) [3 citations]
0.010
0.005
0.000 1880 1900 1920 1940 1960 1980 2000
Year W. B. Scott, The Isthmus of Panama in Its Relation to the Animal Life of North and South America, Science (1916) [3 citations]
9

Probabilistic topicmade by RTM (e ) and LDA + Regression for two documents Top eight link predictions models
(italicized) from Cora. The models were t with 10 topics. Boldfaced titles indicate actual documents cited by or citing each document. Over the whole corpus, RTM improves precision over LDA + Regression by 80% when evaluated on the rst 20 documents retrieved. Markov chain Monte Carlo convergence diagnostics: A comparative review Minorization conditions and convergence rates for Markov chain Monte Carlo Rates of convergence of the Hastings and Metropolis algorithms Possible biases induced by MCMC convergence diagnostics Bounding convergence time of the Gibbs sampler in Bayesian image restoration Self regenerative Markov chain Monte Carlo Auxiliary variable methods for Markov chain Monte Carlo with applications Rate of Convergence of the Gibbs Sampler by Gaussian Approximation Diagnosing convergence of Markov chain Monte Carlo algorithms Exact Bound for the Convergence of Metropolis Chains Self regenerative Markov chain Monte Carlo Minorization conditions and convergence rates for Markov chain Monte Carlo Gibbs-markov models Auxiliary variable methods for Markov chain Monte Carlo with applications Markov Chain Monte Carlo Model Determination for Hierarchical and Graphical Models Mediating instrumental variables A qualitative framework for probabilistic inference Adaptation for Self Regenerative MCMC Competitive environments evolve better solutions for complex tasks Coevolving High Level Representations A Survey of Evolutionary Strategies
Table 2
RTM (e ) LDA + Regression
R
10
Probabilistic topic models
tax credit,budget authority,energy,outlays,tax county,eligible,ballot,election,jurisdiction bank,transfer,requires,holding company,industrial housing,mortgage,loan,family,recipient energy,fuel,standard,administrator,lamp student,loan,institution,lender,school medicare,medicaid,child,chip,coverage defense,iraq,transfer,expense,chapter business,administrator,bills,business concern,loan transportation,rail,railroad,passenger,homeland security cover,bills,bridge,transaction,following bills,tax,subparagraph,loss,taxable loss,crop,producer,agriculture,trade head,start,child,technology,award computer,alien,bills,user,collection science,director,technology,mathematics,bills coast guard,vessel,space,administrator,requires child,center,poison,victim,abuse land,site,bills,interior,river energy,bills,price,commodity,market surveillance,director,court,electronic,flood child,fire,attorney,internet,bills drug,pediatric,product,device,medical human,vietnam,united nations,call,people bills,iran,official,company,sudan coin,inspector,designee,automobile,lebanon producer,eligible,crop,farm,subparagraph people,woman,american,nation,school veteran,veterans,bills,care,injury dod,defense,defense and appropriation,military,subtitle
11
Probabilistic topic models
12

Probabilistic topic models
What are topic models?
What kinds of things can they do?
How do I compute with a topic model?
How do I evaluate and check a topic model? How can I learn more?
What are some unanswered questions in this eld?
13
![Slide: Probabilistic models
This is a case study in data analysis with probability models. Our agenda is to teach about this kind of analysis through topic models. Note: We are being Bayesian in this sense:
[By Bayesian inference,] I simply mean the method of statistical inference that draws conclusions by calculating conditional distributions of unknown quantities given (a) known quantities and (b) model specications. (Rubin, 1984)
(The Bayesian versus Frequentist debate is not relevant to this talk.)](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_014.png)
Probabilistic models
This is a case study in data analysis with probability models. Our agenda is to teach about this kind of analysis through topic models. Note: We are being Bayesian in this sense:
[By Bayesian inference,] I simply mean the method of statistical inference that draws conclusions by calculating conditional distributions of unknown quantities given (a) known quantities and (b) model specications. (Rubin, 1984)
(The Bayesian versus Frequentist debate is not relevant to this talk.)
14

Probabilistic models
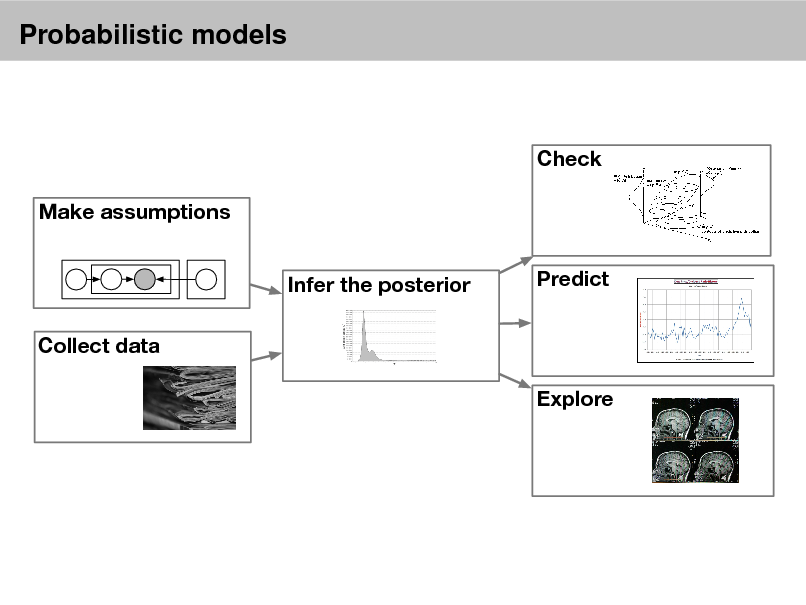
Specifying models
Directed graphical models Conjugate priors and nonconjugate priors Time series modeling Hierarchical methods
Mixed-membership models Prediction from sparse and noisy inputs
Model selection and Bayesian nonparametric methods Approximate posterior inference
MCMC Variational inference
Using and evaluating models
Exploring, describing, summarizing, visualizing data Evaluating model tness
15
Probabilistic models
Check Make assumptions Infer the posterior Collect data Explore Predict
16

Organization of these lectures
Introduction to topic modeling: Latent Dirichlet allocation Beyond latent Dirichlet allocation
Correlated and dynamic models Supervised models Modeling text and user data
3 4
1 2
Bayesian nonparametrics: A brief tutorial Posterior computation
Scalable variational inference Nonconjugate variational inference
5
Checking and evaluating models
Using the predictive distribution Posterior predictive checks
6
Discussion, open questions, and resources
17

Introduction to Topic Modeling
18

Latent Dirichlet allocation (LDA)
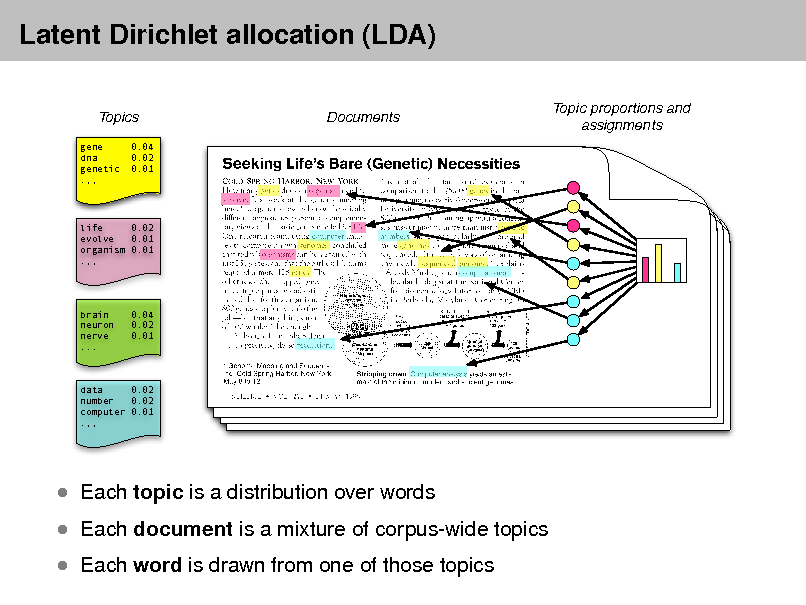
Simple intuition: Documents exhibit multiple topics.
19
Latent Dirichlet allocation (LDA)
Topics
gene dna genetic .,, 0.04 0.02 0.01
Documents
Topic proportions and assignments
life 0.02 evolve 0.01 organism 0.01 .,,
brain neuron nerve ...
0.04 0.02 0.01
data 0.02 number 0.02 computer 0.01 .,,
Each topic is a distribution over words
Each document is a mixture of corpus-wide topics Each word is drawn from one of those topics
20
Latent Dirichlet allocation (LDA)
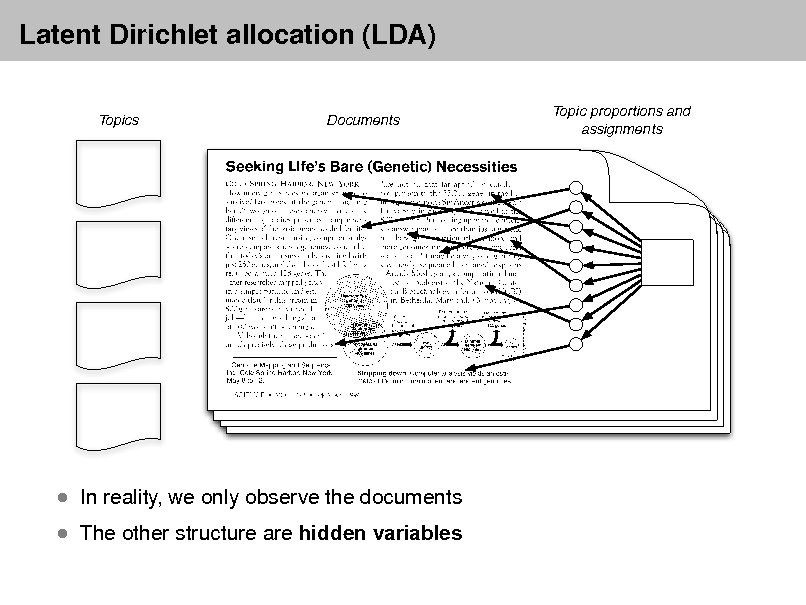
Topics Documents Topic proportions and assignments
The other structure are hidden variables
In reality, we only observe the documents
21
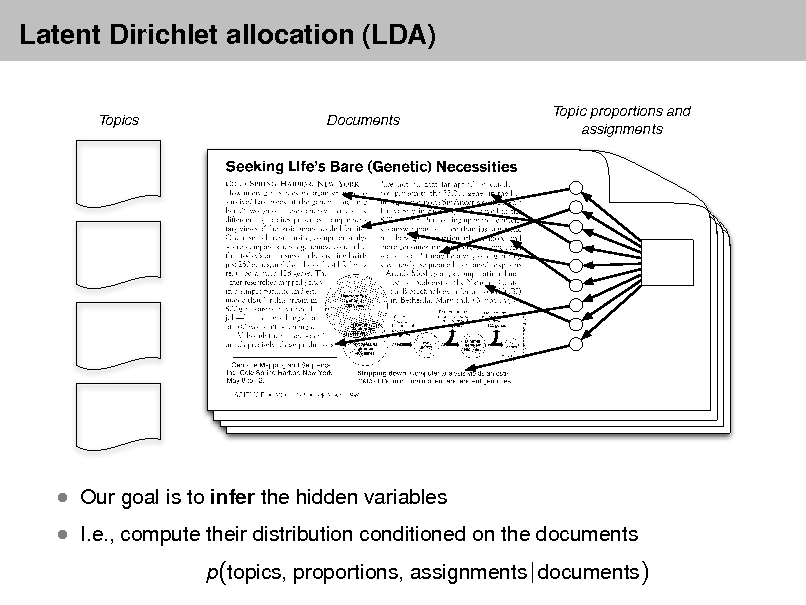
Latent Dirichlet allocation (LDA)
Topics Documents Topic proportions and assignments
I.e., compute their distribution conditioned on the documents
p(topics, proportions, assignments | documents)
Our goal is to infer the hidden variables
22
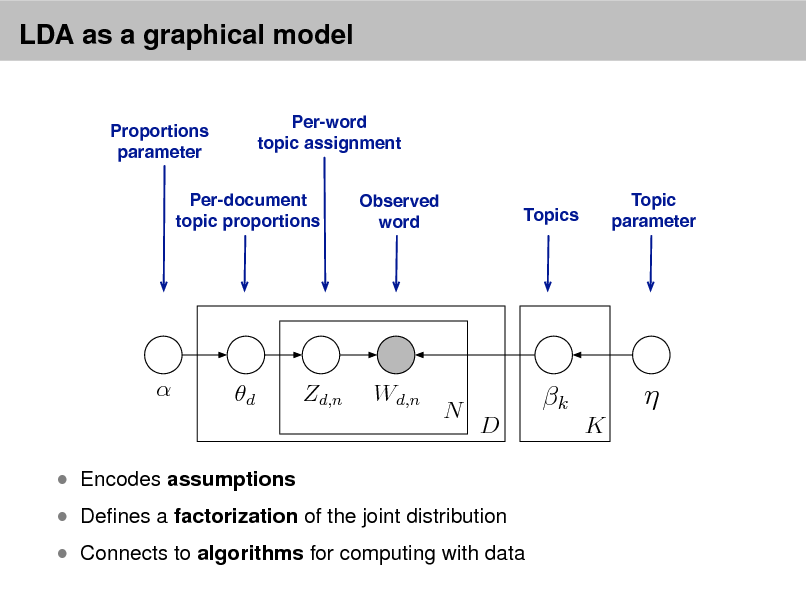
LDA as a graphical model
Per-word topic assignment Observed word Topic parameter
Proportions parameter
Per-document topic proportions
Topics
d
Zd,n
Wd,n
N
k
D K
Denes a factorization of the joint distribution
Encodes assumptions
Connects to algorithms for computing with data
23
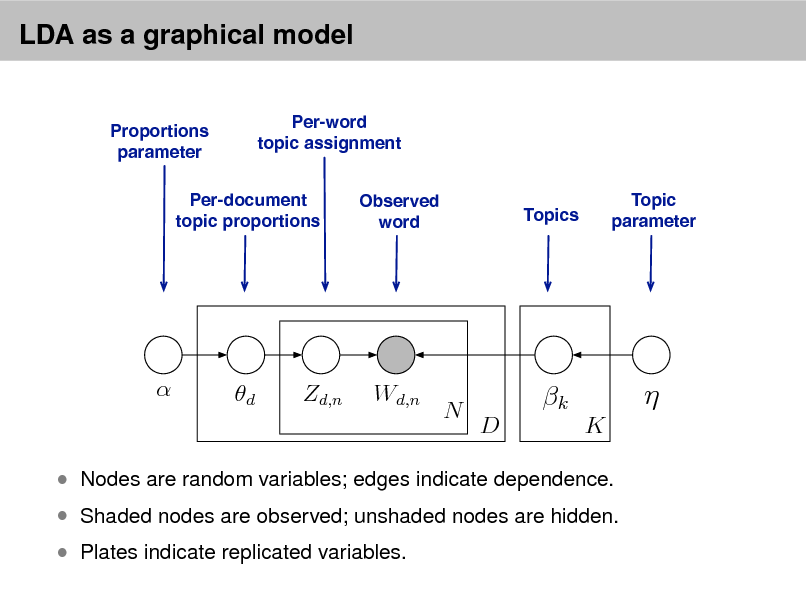
LDA as a graphical model
Per-word topic assignment Observed word Topic parameter
Proportions parameter
Per-document topic proportions
Topics
d
Zd,n
Wd,n
N
k
D K
Shaded nodes are observed; unshaded nodes are hidden. Plates indicate replicated variables.
Nodes are random variables; edges indicate dependence.
24
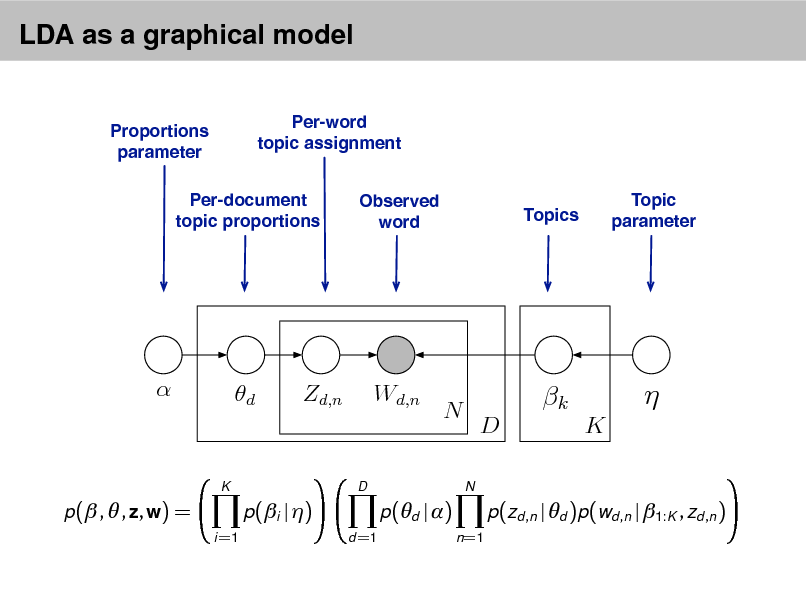
LDA as a graphical model
Per-word topic assignment Observed word Topic parameter
Proportions parameter
Per-document topic proportions
Topics
d
Zd,n
Wd,n
N
N
k
D K
K
D
p( , , z, w) =
i =1
p(i | )
d =1
p(d | )
n =1
p(zd ,n | d )p(wd ,n | 1:K , zd ,n )
25
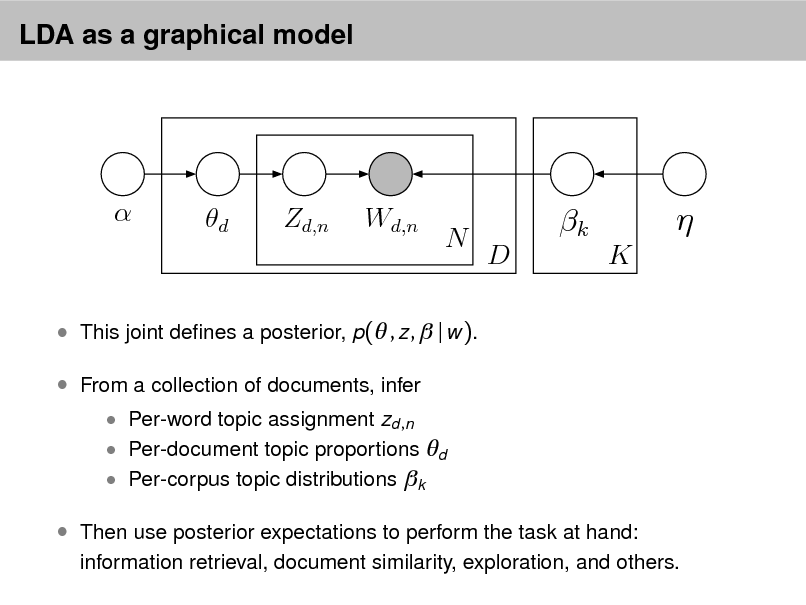
LDA as a graphical model
d
Zd,n
Wd,n
N
k
D K
This joint denes a posterior, p( , z , | w ). From a collection of documents, infer
Per-word topic assignment zd ,n Per-document topic proportions d Per-corpus topic distributions k
Then use posterior expectations to perform the task at hand:
information retrieval, document similarity, exploration, and others.
26
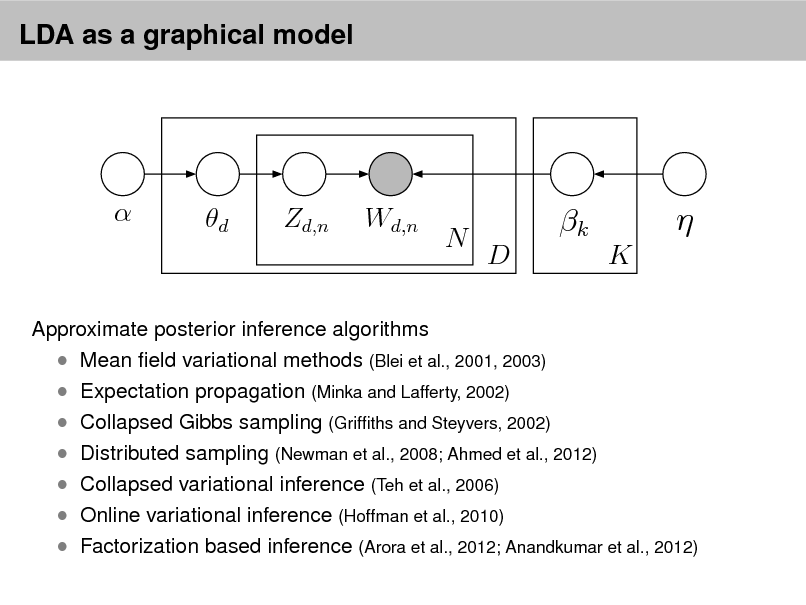
LDA as a graphical model
d
Zd,n
Wd,n
N
k
D K
Approximate posterior inference algorithms Mean eld variational methods (Blei et al., 2001, 2003) Expectation propagation (Minka and Lafferty, 2002) Collapsed Gibbs sampling (Grifths and Steyvers, 2002) Distributed sampling (Newman et al., 2008; Ahmed et al., 2012) Collapsed variational inference (Teh et al., 2006) Online variational inference (Hoffman et al., 2010) Factorization based inference (Arora et al., 2012; Anandkumar et al., 2012)
27

Example inference
Data: The OCRed collection of Science from 19902000
17K documents 11M words
20K unique terms (stop words and rare words removed)
Model: 100-topic LDA model using variational inference.
28
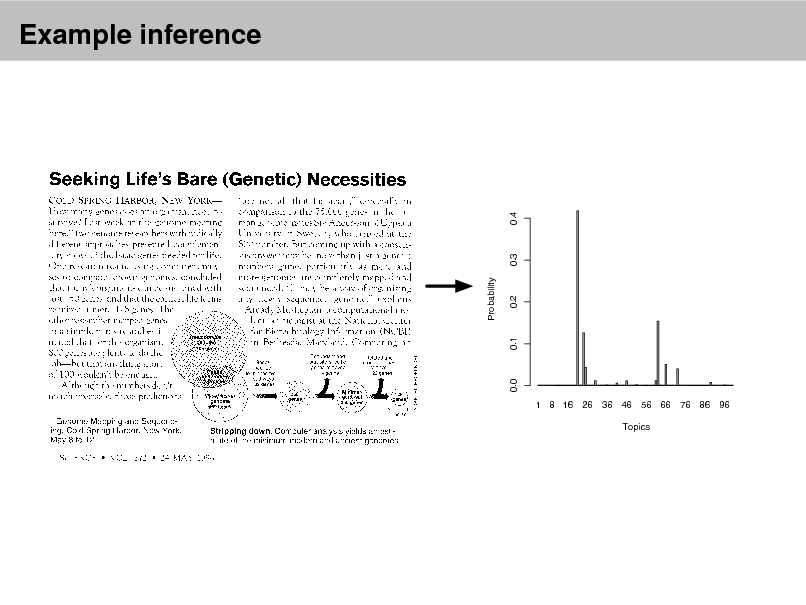
Example inference
Probability
0.0
1 8 16 26 36 46 56 66 76 86 96 Topics
0.1
0.2
0.3
0.4
29

Example inference
Genetics human genome dna genetic genes sequence gene molecular sequencing map information genetics mapping project sequences Evolution Disease evolution disease evolutionary host species bacteria organisms diseases life resistance origin bacterial biology new groups strains phylogenetic control living infectious diversity malaria group parasite new parasites two united common tuberculosis Computers computer models information data computers system network systems model parallel methods networks software new simulations
30
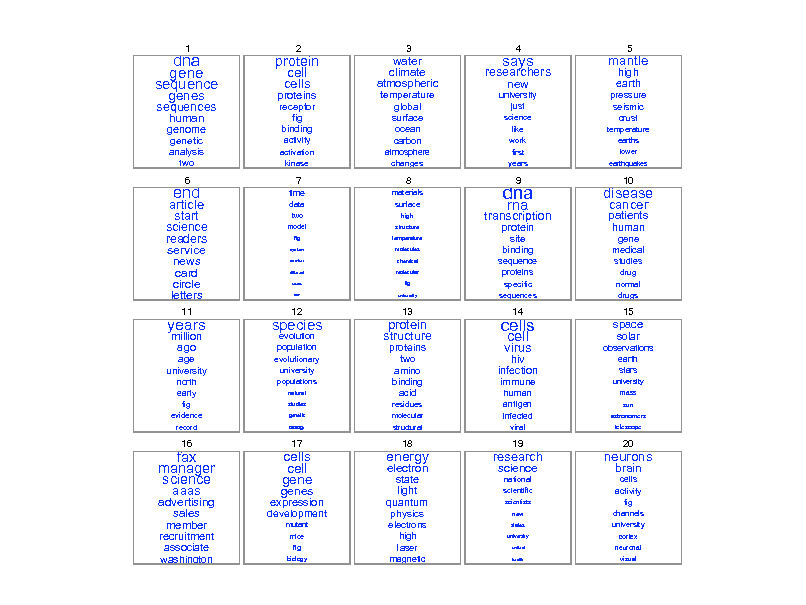
dna gene sequence
sequences
genome
genetic analysis
two
1
protein cell
proteins
receptor fig binding
activity
activation kinase
2
3
genes
human
cells
water climate atmospheric
temperature global surface
ocean carbon
atmosphere changes
researchers new
university just
science like work first years
says
4
mantle
high earth
crust
temperature earths
lower
earthquakes
5
pressure seismic
science readers service news
card circle letters
11
article start
end
6
7
time
data
two
model
fig
system
number
different
results
rate
8
materials surface
high
structure
temperature
molecules
chemical
molecular
fig
university
dna
transcription
protein
site binding
specific
sequences
9
rna
disease
patients human
gene medical studies
drug normal drugs
10
cancer
sequence proteins
years
age university
north early fig
evidence
record
million ago
species
evolution population
evolutionary university
populations
natural studies
genetic
biology
12
protein structure
proteins
two amino binding
acid
residues
molecular
structural
13
cells
hiv infection
immune
human antigen infected
viral
14
15
virus
cell
space
solar
stars
university
mass
sun
astronomers telescope
observations earth
fax manager science
advertising sales member recruitment
associate washington
16
aaas
development
mutant
mice
fig
biology
expression
genes
cells cell gene
17
energy
state light quantum
physics
electrons high laser
magnetic
18
electron
research
science
national
scientific
scientists
new
states
university
united
health
19
neurons
brain
cells activity fig
20
channels university
cortex
neuronal
visual
31

Aside: The Dirichlet distribution
The Dirichlet distribution is an exponential family distribution over the
simplex, i.e., positive vectors that sum to one p( | ) =
i
i
i
i (i )
i
i 1
.
It is conjugate to the multinomial. Given a multinomial observation, the posterior distribution of is a Dirichlet. The parameter controls the mean shape and sparsity of . The topic proportions are a K dimensional Dirichlet.
The topics are a V dimensional Dirichlet.
32
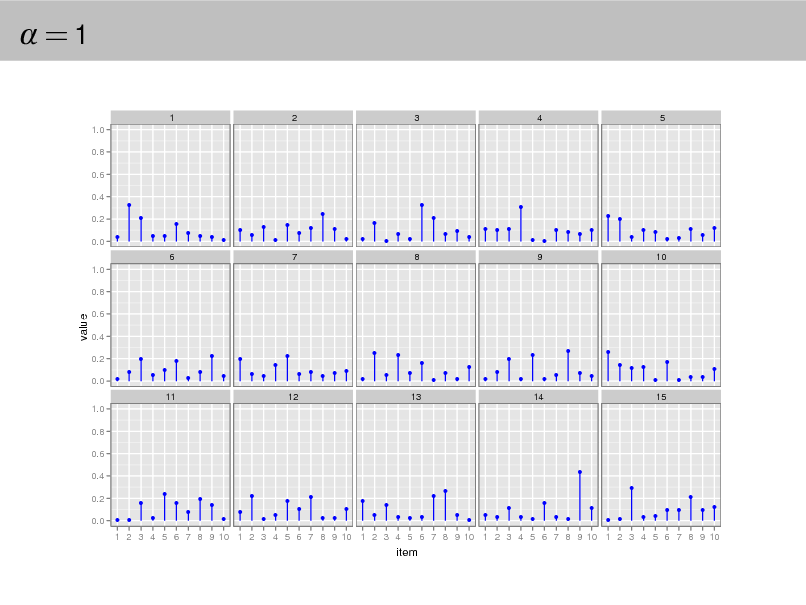
=1
1 1.0 0.8 0.6 0.4
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
2
3
4
5
0.2 0.0 1.0 0.8
6
7
8
9
10
value
0.6 0.4 0.2
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
0.0 1.0 0.8 0.6 0.4 0.2 0.0
q
11
12
13
14
15
q q q q q q q q q q q q q q q q q
q q q q q q q
q q q q
q q q q q
q q q q
q q q q q q q
q q q q q q
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
item
33
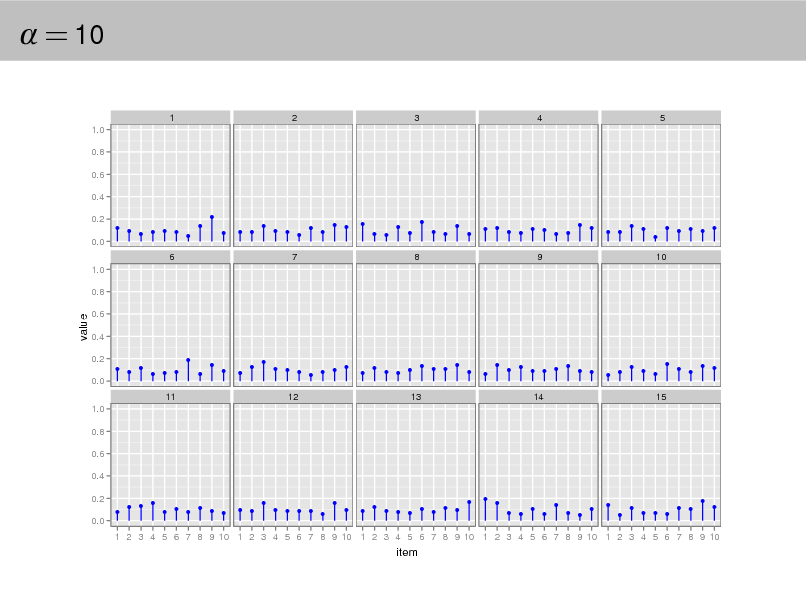
= 10
1 1.0 0.8 0.6 0.4 0.2
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
2
3
4
5
q
q
q
q
q
q
q q
q
q
q
q
q
0.0 6 1.0 0.8
7
8
9
10
value
0.6 0.4 0.2
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
q
q
q
q
q
q
q
q
0.0 11 1.0 0.8 0.6 0.4 0.2
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
12
13
14
15
q
0.0
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
item
34
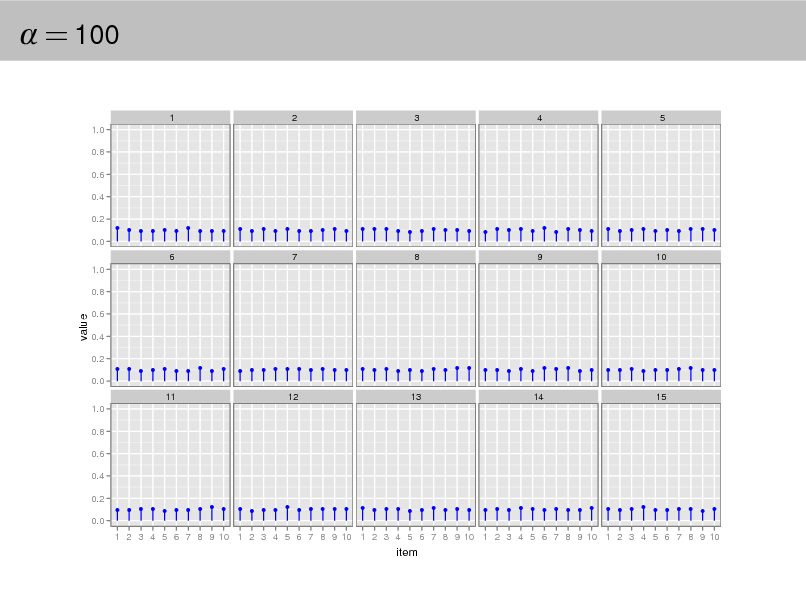
= 100
1 1.0 0.8 0.6 0.4 0.2
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
2
3
4
5
0.0 6 1.0 0.8 7 8 9 10
value
0.6 0.4 0.2
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
0.0 11 1.0 0.8 0.6 0.4 0.2
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
12
13
14
15
0.0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
item
35
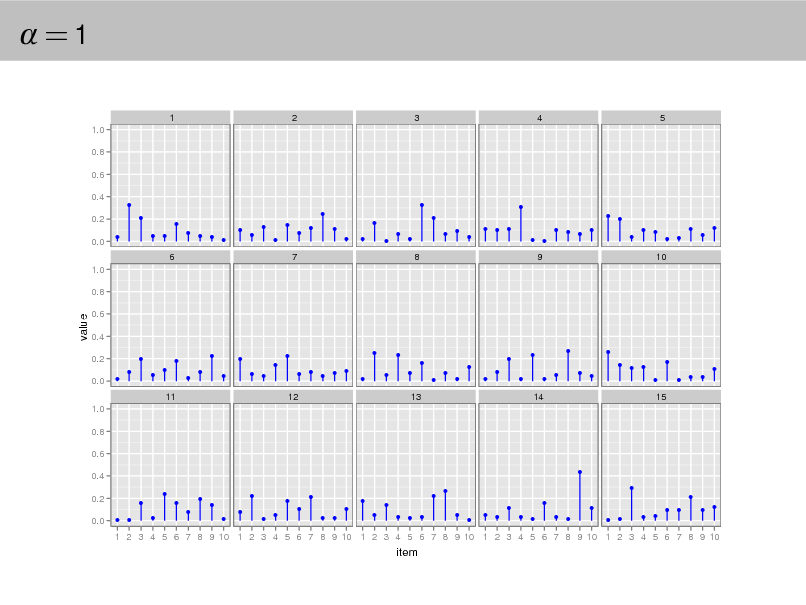
=1
1 1.0 0.8 0.6 0.4
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
2
3
4
5
0.2 0.0 1.0 0.8
6
7
8
9
10
value
0.6 0.4 0.2
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
0.0 1.0 0.8 0.6 0.4 0.2 0.0
q
11
12
13
14
15
q q q q q q q q q q q q q q q q q
q q q q q q q
q q q q
q q q q q
q q q q
q q q q q q q
q q q q q q
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
item
36
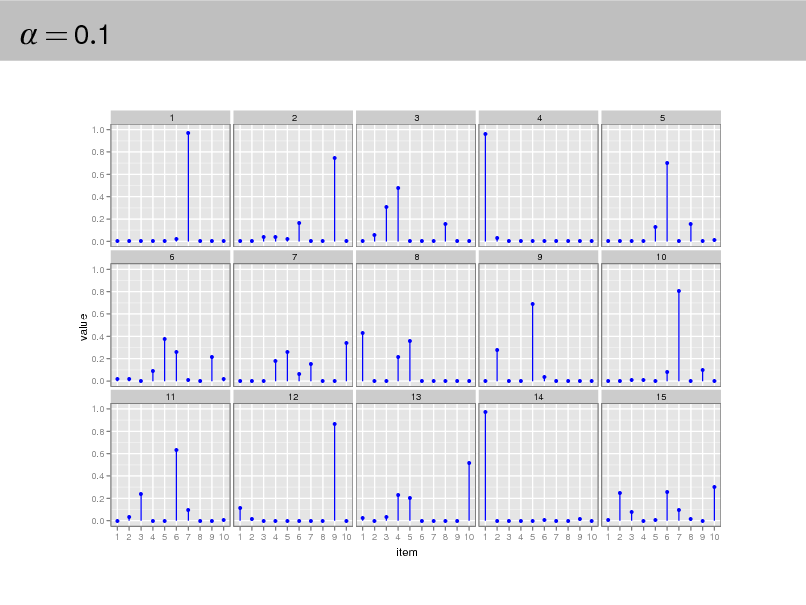
= 0.1
1 1.0 0.8 0.6
q q
2
3
q
4
5
q
q
0.4
q
0.2 0.0 1.0 0.8
q q q q q q q q q q q q q q
q q q q q q q q q
q q q q q q q q q q q q q q q q
q q
q q q
6
7
8
9
10
q q
value
0.6 0.4 0.2
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
0.0 1.0
q
q
q
q
q
11
12
q
13
q
14
15
0.8 0.6 0.4 0.2 0.0
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
item
37
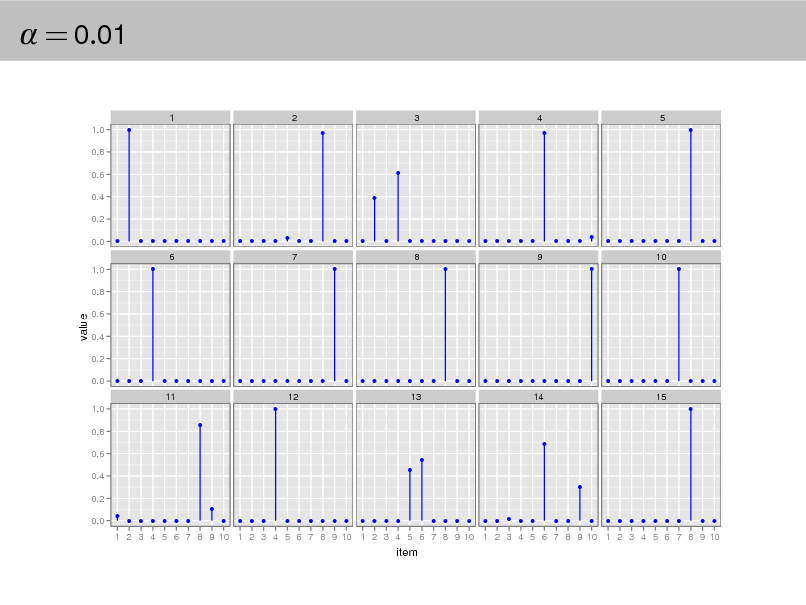
= 0.01
1 1.0 0.8 0.6 0.4 0.2 0.0 1.0 0.8
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
2
q
3
4
q
5
q
6
q
7
q
8
q
9
q
10
q
value
0.6 0.4 0.2 0.0 1.0
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
11
q
12
13
14
15
q
0.8
q
0.6
q
q
0.4
q
0.2
q
0.0
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
item
38
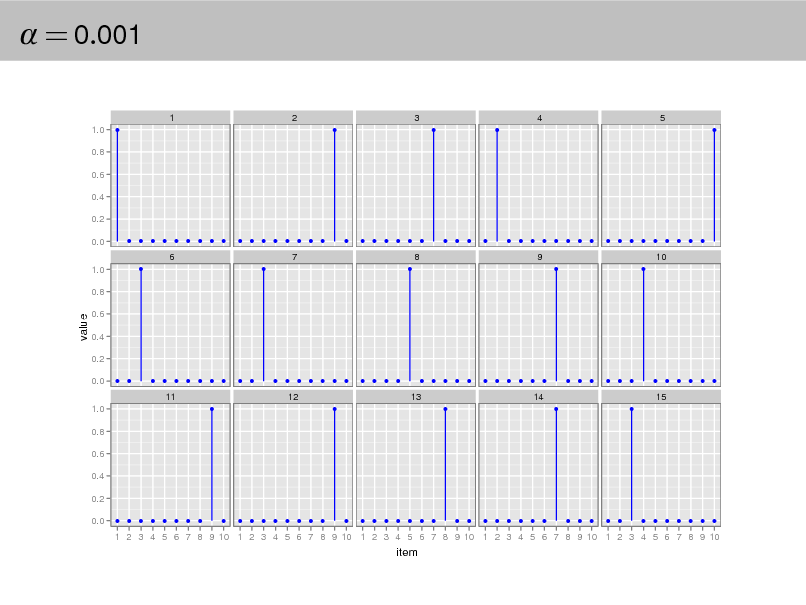
= 0.001
1 1.0 0.8 0.6 0.4 0.2 0.0 1.0 0.8
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
2
q
3
q q
4
5
q
6
q q
7
q
8
9
q q
10
value
0.6 0.4 0.2 0.0 1.0 0.8 0.6 0.4 0.2 0.0
q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q
11
q
12
q
13
q
14
q q
15
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
item
39

Why does LDA work?
LDA trades off two goals.
1 2
For each document, allocate its words to as few topics as possible. For each topic, assign high probability to as few terms as possible.
These goals are at odds.
Putting a document in a single topic makes #2 hard:
All of its words must have probability under that topic.
Putting very few words in each topic makes #1 hard:
To cover a documents words, it must assign many topics to it.
Trading off these goals nds groups of tightly co-occurring words.
40
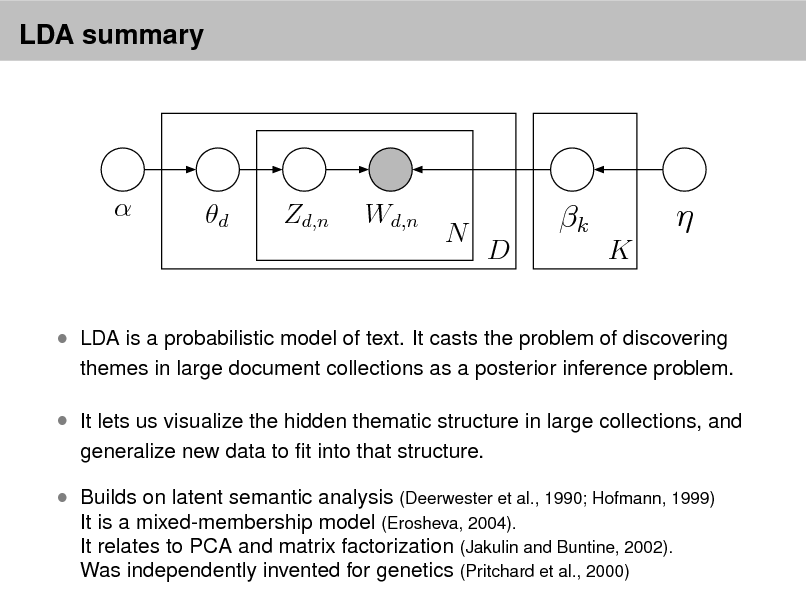
LDA summary
d
Zd,n
Wd,n
N
k
D K
LDA is a probabilistic model of text. It casts the problem of discovering
themes in large document collections as a posterior inference problem.
It lets us visualize the hidden thematic structure in large collections, and
generalize new data to t into that structure.
Builds on latent semantic analysis (Deerwester et al., 1990; Hofmann, 1999)
It is a mixed-membership model (Erosheva, 2004). It relates to PCA and matrix factorization (Jakulin and Buntine, 2002). Was independently invented for genetics (Pritchard et al., 2000)
41
![Slide: SYMBOL DESCRIPTION by emerging groups. Both modalities are driven by the McCallum, Wang, & Corrada-Emmanuel git entity is group assignment in topic t common goal of increasing data likelihood. Consider the tb topic of an event b voting example again; resolutions that would have been as(b) signed the same topic in a model using words alone may wk the kth token in the event b t Process Compound Dirichlet topics (b) be assigned to dierent Process if they exhibit distinct voting Vij entity i andAllocation Author-Topic Model Author-Recipient-Topic Model Latent Dirichlet js groups behaved same (1) Author Model (AT) (ART) (LDA) (Multi-label Mixture Model) patterns. Distinct word-based topics may be merged if the April 21-25, 2008 Beijing or [Blei, Ng, Jordan, 2003] on the Track: Data Mining - Modeling Smyth 2004] dierently (2) Chang, Blei WWW 2008 / Refereed event b n, and the [Rosen-Zvi, Grifths, Steyvers, [This paper] [McCallum 1999] entities vote very similarly on them. Likewise, multiple difS number of entities ve masses models are considerably r more computationally ex ! a a a ferent divisions of entities into groups are made possible by T number of topics ! Also, like LDA and PLSA, they will not be able t conditioning them on the topics. guish between topics corresponding to ratable asp G number of groups " z x global topics representingx properties of the review " " The importance of modeling the language associated with B number of events $ In the following section we will introduce a metho interactions between people has recently been demonstrated explicitly models both types of topics and ecient V number of unique words ! " ! " z z z ds. Then, ratable aspects from limited amount of training da in the Author-Recipient-Topic (ART) model [16]. In ART A A,A number of word tokens in the event b y z Nb z it is used the words in a message between people in a network are $ # $ # $ # Sb number of entities who participated in the# event bw 2.2 $ MG-LDA w w w nite numWe propose a model called Multi-grain LDA (MG T A T T generated conditioned on the author, recipient and a set N N N N which models two distinct types of topics: global to is drawn w # w of specify that describes the message. The model thus cap- N topics D D D local topics. As in PLSA and LDA, the distribution D N K to topics is xed for a document. However, the distrib z1 tures both the network structure within which2: the people Table 1: Notation used in this paper (a) of words local topics is allowed to vary across the document. Figure A two-document segment of the RTM. The variable y indicates whether the two documents are linked. The complete model (b) interact as well as the language associated contains this variable for each pair of documents. The plates indicate 1: Three related models,words andthe ART model. In all models, each observed either from the mixture with the interin the document is sampled word, Figure replication. This model captures both the and the link stribution, structure of the data shown in Figure 1. Figure 1: (a) LDA model. (b) MG-LDA model. topics specic to a particular z2 z3 w,:laid generatedt modelsa multinomial wordexis This provides an inferential speed-up that makes it from at varying granularities. As distribution, z , or from the mixture of local topics specic actions. In experiments withmodel for the focused topic model Figure 1. Graphical Enron and academic email, possible to local context of the word. The hypothesis is that and is set of one ! " journal might & the ART model is able to discover role !D formulation, inspired by the supervised LDA model (Blei ument,topic/author, Notehowever ] topics are selected dierently in each captured models.topics and glob similarity of 2007), ensures that the same latent topic as- each word ineachaamples,multinomial parameters,bed,nfor people aspects will be of the by local t document. z, articles [zon = exchangeable within and McAuliffe that Eq which .% is still not an issue, an assumptiong the number of documents directly dependent d,n than In therefore, z model is sampledmore realistic data, overLDA, the they are exchangeableisby from a from topic distribution, reviewed items. signments used to generate z :phrases better than 3. Related Modelsconsider network connectivity the content of4 the documents Minimizing:inthe relative thetopic is not expected to suerper-documentwill capture properties of, whichLondonFor exam SNA models that and, one where year. 5 entropy is equivalent to maximiz- Other hotel: . S Dirichlet over topics. Insider an extract Model, there a also generates their link structure. Models which do not Parse trees is as approach is to use the Author from a review of is tting. Another news,the marginal a periods T without Jensens lower bound on might experience a Markov alone. However, the ART model does not explicitlycoupling, such as Nallapati et al. (2008), might ing thein turn such sampled fromprobability ofof time chain Monte transport in London is straightforward, the tube s enforce this capture any associated with each Carlo algorithm for inference with LDA, as proposed in category), and authors are sampled grouped into M the observations, i.e., the evidence lower bound dDTM requires represent- [14]. Titsias !T one topic observation. While the (ELBO), author (or about an 8 minute walk . . . or you can get a bus for & subsetsone for groups formed by(2007) introduced the innite dgamma-Poisson into two independent :some entities in#k network. divide the topics prothe z5 z6 describe a modicationthese periods, :mind ing all topics In section 3 we will for the discrete ticks within of this sampling documents can be viewed a mixture of cess, a distribution over unbounded links and the of nonmatrices other for words. Such a decomposition preuniformly.cDTM theanalyzed such)] +LDAmodel, the topic isItsampled fromas aper-authortopic London sh In d ,d Author-Topic model. theq [log p(ycan |zd , z , , data without a sacrice L = (d for) E proposed Multi-grain method ,d the o Eq. 1. GT model simultaneously clusters entities to groupsmaking meaningful predictions The ! # ), " models from w LDAmemory or speed. With , and$the granularity repof and negative and used it as the basisvents these given words for topic multinomial distribution,the cDTM, authors are sampledthe entire review (words: London, tube, contex uniformly from the observed Both E v PLSA| , z )] + the bag-of-words methods use a(, clusters wordsintegers,topics, unlike models athat model and words given links. In Secratable aspect location, specic for the local about links d n q [log p(wd,n maximize and 1). generchosen to 1:K d,n z7 :his :for resentationcan be S 2 can only explore N of the documents BGmodel tness rather than 2 list bd nof q documents,)] therefore they In the Author-Recipient-Topic model, there is bus). Loc of images.into this $k model, the distribution4over featuresempirically that the RTM outpersentence (words: transport, walk, tion we demonstrate E [log p(zd,n |d + authors. T ' In , co-occurrences atcomputational complexity. This is ne, provided to limit bthe document level. ate topics solely based on word distributionsforms suchas Latent tasks. are expected to be selection of these a separatenote d |)] theH(q),overall topic ofnot thedocument, topic-distribution for each author-recipient pair, and the reused between very dierent for the mth image is given by a Dirichlet such modelsover distribution onM Eq [log represent an p( + (4) the goald isWe to that cDTM and dDTM are the only items, whereas global topics will correspond only t Dirichlet Allocation [4]. In this way the GT model innite discov% but our goal is:years B to is determined from the observed author, and by uniformly samdierent: time into consideration. Topics topic-distribution takeextracting ratable aspects. The the non-negative elements of the mth row INFERENCE, ESTIMATION, AND topic models 3 of the ular types of items. In order to capture only genu where (d1 , d2 ) denotes all document pairs. The rst term main topicover all the reviews for a particular item is virtuof time models (TOT) [23] and dynamic mixture ers salient topics relevant to relationships parameters entities pling a recipient from the set of topics, we gamma-Poisson process matrix, with between proporof the ELBO differentiates the RTM from LDA (Blei et al. recipients for the document. allow a large number of global topics, e PREDICTION Graphical ally the same: review of also item. timestamps when Figure models include (a) Overall Graphical Model (b) Sentence Graphical Modela (DMM) [25] this affect theTherefore, in the such 1: creating model representation of the obin Eq. 1. social networktopics which the models model dened, we turn to approximate poste- 2003). The connections between documents The TOTtomodel treats the of cDTM. The evolutionaofbottleneck at the levelisof local topics. O the tional to the values at these elements. While the that only this results in the analysis of documents. model a collection topic modeling methods are applied reo Figure 1: approximate posterioras observations ofbelow, in topics, while governed by Brownian motion.topic parameters istthe purposes. Other With this bottleneck is specic to our jective in The Group-Topic inference (and, The st time stamps views for dierent items, they inferthe latentcorresponding to topics a sparse unable to detect. examine words arematrix of distributions, the number inference, entries estimation, and prediction. We parameter estimation). assumes that the topic mixture proportions of observed time stamp of document d .variablemodels conceivably migh rior of zero parameter tions of multi-grain topic DMM t distinguishing properties of these items. E.g. when applied the bottleneck reversed. Finally, we note that our d Figure the the matrix of the GT model values of the STM, a in any columncapabilities is model develop variationalap-document is made up We a number ofof procedure under these models topic mixWe demonstrate 1: In of thegraphical correlated witha the byWeinference procedure for aapproximat- of develop the inferencesentences, the assumption are likely to ineach hotel is dependent on previous to a collection documentreviews, ing the posterior. use this of is observed. To discretized. is simply its w. These words for each Newyd and ei- a youth hostels, d, In represented by a voting data: one from US with (EM)procedure infor variational generative processwill beFrance,documenthotels, the topics A drawback ofmulti-grain that time generate of granularit only topics: ture proportions. are(i.e.,TOT is DMM, fer observed links in modeled York of thelarge sets of tree of latent topics z which in turn generate wordson thatbill). Thehotelstopics of both are,dsampledset of authors, ad , the dDTM isprinciple is for two-levelsis nothing pr non-zero entries. Columns whichexpectation-maximization have entries Senalgorithm parameter plying it to two and local. In though, there a or, similarly,elementsfor ,to a collection of from themselves this each ther 1 or unobserved).1whenis chosen and the time from this If the chosen by will not typically (as encoded by the same or not word, an author xdo are constant, uniformlyinformation is set, resolution is chosen to be too coarse, then the a We applied V values the topic of their parent Therefore, UN. how a tree), the topic weights for(b) document two reasons.In the setting Mp3 players then a topic z is selected from a ate and thelarge the from the Generalbe sparse.weights estimatedshowclarity, binomial distributionof these. toOurisdiscover them.to issummarized iPod athe model described timethis are ex-a from extending other nodes parents successorestimation. Finally,this can be usedmodel whose parame- distribution used y better 1notationlink the author,we assumption that documents within a in step section Assembly of the we ters have been . (For as predictive dependencies one gi j that= will infer topic specic is like here, and then will levels. is If the resolution is too word w One might expect that a anot all model First,reviews,cangx modelsin whenever atopicsob- reviews of changeable two not be true. generated from for other tasks ev while and sentence nodes d ,d arexinterested Zen player. Though these or The model model will not decouple across-data variables andlinks. si- within the documentthebetween d1 of Creative distribution this However, asne, then the number of variational none of will exclusters voting entities intoprevalence for withincoalitions sentences in Table 1, andserved reviewson themodelinferring evolving topics. ofare all valid and d2 set y = levels of granularity could be benecial. topic-specic multinomialthedpaper is otherwise, z . follows. Inthe deare shown.) of topics. In the ICD of words and and plate inappropriatenotright, whereratable aspects, but rather described previously, parameters these graphical andcorpora,d as 0 organized of representation topics,is The rest ofrepresent the absenceas they do in secdata proportionsThe structure of the number of zero approach points are added. Choosing the disWe represent document as a set multaneously discovers topics for word attributes the sentence Some seek tois shown ain ne is be construed asdescribe themessageinto specic types. plode as more timebe a decisionabased on assumptions of sliding windo is cannot suitabletion 2 we evidence for y ,d = In demonstrated by an automatic parse of describing laid in his mind 1.for of the The dDTM and data. Inference we phrasesmodels linkFigure for years.reviewedd items 0.develop the cDTM ete(m ). clusterings modeling In cretization covering T adjacent sentences within it. Each wind should entries is controlled by a separate process, posteriorIndistributioninference, model compute the IBP,posterior from the variables condiin detail. thesefurther discussion we will refer to an and inas global cases, treating these Section 3 sender topics the).relationsSTM assumes that the tree structure and wordsnd of the latentWithout consideringmessage linksof unobserved variables is by general more the data. one recipients. Weconcerns (bills or resolutions) between entities. We are given, but the latent topics z are not. has asone presentssuchecient posterior in-topics, than However, the computational distribution over loc zmi the correspondanthe cDTM property treat- about document d has an associated the values of the non-zero entries, whichtionedcontrolled by Exact posterior inference is in- An email totheytopic semanticsaofglobalbased on sparse varia-object prevent analysis at the appropriate time could are on the observations. ference algorithm for event, or to of the loc morebecause the underlying data. For might scale. d,v and that the groups obtained from the GT model are et al. 2003; Blei and McAuliffe 2007).treat in a faithful review, networksthe sectiontheor base topic, the of the message, a distribution dening preference for loc tractable (Blei signiWe In and then the in the sender reecting a single the example, in large social methods.its brand4, we presentauthors ing all events both corpus tionalsuchtwo such as Facebook the ab-ofexperimental Dis- we develop the continuous timeemploytopiccan be sampled u as andas news recipients as operation. Thus, versus global topics d,v . A word the gamma random variables. dynamic results on corpora. covering topics two people does with ratable aspects, such as sence of a link between that correlate not necessarily author and the cantly more cohesive (p-value < .01) than appeal to variational methods. those obtained does part of window of the its sentence s, where ecause the simplied AT model, butthe right not distinguish the becomes model recipients modeling sequential time-series model (onlytheythisnot location may Figure much more problem- (cDTM) for coveringmessage, which the window i cleanliness mean that be real is 1) The sparseto be model (SparseTM, Wang & Blei, 2009)we preposition of. undesirable inare andfriends;ittheyfor hotels, friends A manager may arbitrary granularity. The cDTM can be according to a a secretary and from the Blockstructures amodel.consistent as the object of theposit a by free of distributionsThematically, manyothers existence in the model [17]. topics are with send email tocategorical distribution s . Importa model also disis going topic noun The GT In variational methods, indexed family variationalispa- the stochastic eachorreal-world situations. these To data because ismethods. Most PLSA istribution are with of Blockstructures network.of equivalent to who aticunaware LDAContinuousin dynamic topic over the latent variables fact limit the dDTM at overlap, permits to exploit seen as a natural that of thewindows its nest pos2 Australia time Treating this in some way in every requests present the nature it a travel brochure, slab model expect UNThose parameters covers new uses a nite spike and we wouldto ensure that each topic are as be close to thevice versa, butlink asor models of thereview. Therefore, a is dicult resolution, be quite dierent. Even rameters. and Senhe number and more salient topics in both the to see words such t to Acapulco, Costa Rica,theunobserved better respects our lack ofand language used maythe resolution at which the document techniques are co-occurrence domain. These simple sible match the true Blockstructures model, each event to discover status of using only co-occurrence information is representedkitchen, distribution over words.Our model can relative entropy. knowledge aboutregularities relationship. quantity of re- email that we receive; modeling more posterior, where The more than by a with topics discovered closeness is these kinds of them by their the large denes junk at and of modeling ate datasetsin comparisonsparsedebt, or pocket. by (1999) for measured by capturemore dramatically, consider thistwo exceedingly groups time stamps are measured.local topics withoutthe expensive mo only rely nite, document In See a single et al. lationship, e.g., of the treating in level.event case entities large amounts the topics about as authors 15, 33, spikes arethem exploit generated by Bernoulli draws withJordanfamily,topic- a review. We use the fully- Second, trainingIn athe links undistinguished awe would liketopics we write transitions usedinin [5, would 32, 28, 16]. Intr topics whether non-linksis stampedhidden decreases as from the num- cDTM, we still represent topics their natural these messages as as document collection, very large In the time needed and of data The topic examining the words of in predictive problems. topics are the resolutions, thefactorized GT computational cost of inference; since the linkas well our model a variables are of a symmetrical Dirichlet prior Dir() for the dist behave the same or in the graphicalmodel Even can hand, inthere is a danger that not. On K. its latent undesirable parameterization, but we use Brownian motion [14] to to topics as wide parameter. The topic distribution is then drawn from a ber of topics the other this casechanging through the or roles. leaves model they in semantic be extremely confounding and be removed when- since they do not reect our to control smoothness of topic transition wn from split or joinedefforts to capture local syntactic ) = [q (d |d ) qz (zd,n |d,n )] , space models [6]coursebe overown byInvery ne-grain globala topics theirs permits expertise i, j (j > i > Previous together as inuenced q(, Z|, context and similarity either a symmetric Dirichlet distribution dened over these votersinclude by the spikes. evolution news data, for (3) have the model will of the d n relationsuccessfullymultiple attributes (whichstoriesour example, by be two arbitrary time indexes, s and s be the time may Alternatively we could collection. as the in associated with model model. through time. Let exper- 0) ignoring the recipient information single functions from dependency parses [7]. i j bm . The over resultingtopic , d that document topics are employ range (d still be ordetermine words change intersection of model patterns of behavior. derived spike and slab approach, isbut allowsThese methods each doc- overSumsthewhich a link pairsbeenwill )will understood to the AT globalatopics and The be the elapsed time between them. formal denition of the model with K gl glo The ICD also uses a stamps, iments of email pairs describing The discrete-timefor hotels by it aspects, likeevent, generated New and treatinghaswith email location dynamic topic it and share similar contexts, but do not where a set of Dirichlet parameters, one for are the wordsfordifculty eachobserved. exchangeable topic inifmodelonly ahas ones ,s local topics is the following. First, draw K account for thematic consistency. They have ratable develop. thepol- document asmodel to York. K-topic cDTM model, the distribution of thethis topic proK locauthor. However, in kth (dDTM) the an unbounded number of as y,(due to the IBP) and a an insect or a term from We is similar tobuilds LDA model) we areislosing all information about the recipients, from a Dirich per-topic multinomial). show in Sectionon that thisthe dDTM, documents In k K) topics parameter at global is: ysemous words such spikes which can be either baseball. With the 4 a sense case (which will provide such machinery [2]. In hypothesis conrmed distributions for term w topics gl z (1 arse set of
LDA summary
d
d
d
d
d
d'
d,n
d,d'
d',n
d
d
d
d
d,n
k
d',n
d
d'
w1
w2
w3
w4
w5
1
2
1
2
1
2
w5
w6
w7
LDA is a simple building block that enables many applications.
1 2 1 2 1 2 1 2
It is popular because organizing and nding patterns in data has become
important in the sciences, humanties, industry, and culture.
Further, algorithmic improvements let us t models to massive data.
1 1 2
j i
2. GROUP-TOPIC MODEL(due to the shared gamma more globally informative slab
experimentally.
Dir( gl ) and K loc word distributions for local top](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_042.png)
SYMBOL DESCRIPTION by emerging groups. Both modalities are driven by the McCallum, Wang, & Corrada-Emmanuel git entity is group assignment in topic t common goal of increasing data likelihood. Consider the tb topic of an event b voting example again; resolutions that would have been as(b) signed the same topic in a model using words alone may wk the kth token in the event b t Process Compound Dirichlet topics (b) be assigned to dierent Process if they exhibit distinct voting Vij entity i andAllocation Author-Topic Model Author-Recipient-Topic Model Latent Dirichlet js groups behaved same (1) Author Model (AT) (ART) (LDA) (Multi-label Mixture Model) patterns. Distinct word-based topics may be merged if the April 21-25, 2008 Beijing or [Blei, Ng, Jordan, 2003] on the Track: Data Mining - Modeling Smyth 2004] dierently (2) Chang, Blei WWW 2008 / Refereed event b n, and the [Rosen-Zvi, Grifths, Steyvers, [This paper] [McCallum 1999] entities vote very similarly on them. Likewise, multiple difS number of entities ve masses models are considerably r more computationally ex ! a a a ferent divisions of entities into groups are made possible by T number of topics ! Also, like LDA and PLSA, they will not be able t conditioning them on the topics. guish between topics corresponding to ratable asp G number of groups " z x global topics representingx properties of the review " " The importance of modeling the language associated with B number of events $ In the following section we will introduce a metho interactions between people has recently been demonstrated explicitly models both types of topics and ecient V number of unique words ! " ! " z z z ds. Then, ratable aspects from limited amount of training da in the Author-Recipient-Topic (ART) model [16]. In ART A A,A number of word tokens in the event b y z Nb z it is used the words in a message between people in a network are $ # $ # $ # Sb number of entities who participated in the# event bw 2.2 $ MG-LDA w w w nite numWe propose a model called Multi-grain LDA (MG T A T T generated conditioned on the author, recipient and a set N N N N which models two distinct types of topics: global to is drawn w # w of specify that describes the message. The model thus cap- N topics D D D local topics. As in PLSA and LDA, the distribution D N K to topics is xed for a document. However, the distrib z1 tures both the network structure within which2: the people Table 1: Notation used in this paper (a) of words local topics is allowed to vary across the document. Figure A two-document segment of the RTM. The variable y indicates whether the two documents are linked. The complete model (b) interact as well as the language associated contains this variable for each pair of documents. The plates indicate 1: Three related models,words andthe ART model. In all models, each observed either from the mixture with the interin the document is sampled word, Figure replication. This model captures both the and the link stribution, structure of the data shown in Figure 1. Figure 1: (a) LDA model. (b) MG-LDA model. topics specic to a particular z2 z3 w,:laid generatedt modelsa multinomial wordexis This provides an inferential speed-up that makes it from at varying granularities. As distribution, z , or from the mixture of local topics specic actions. In experiments withmodel for the focused topic model Figure 1. Graphical Enron and academic email, possible to local context of the word. The hypothesis is that and is set of one ! " journal might & the ART model is able to discover role !D formulation, inspired by the supervised LDA model (Blei ument,topic/author, Notehowever ] topics are selected dierently in each captured models.topics and glob similarity of 2007), ensures that the same latent topic as- each word ineachaamples,multinomial parameters,bed,nfor people aspects will be of the by local t document. z, articles [zon = exchangeable within and McAuliffe that Eq which .% is still not an issue, an assumptiong the number of documents directly dependent d,n than In therefore, z model is sampledmore realistic data, overLDA, the they are exchangeableisby from a from topic distribution, reviewed items. signments used to generate z :phrases better than 3. Related Modelsconsider network connectivity the content of4 the documents Minimizing:inthe relative thetopic is not expected to suerper-documentwill capture properties of, whichLondonFor exam SNA models that and, one where year. 5 entropy is equivalent to maximiz- Other hotel: . S Dirichlet over topics. Insider an extract Model, there a also generates their link structure. Models which do not Parse trees is as approach is to use the Author from a review of is tting. Another news,the marginal a periods T without Jensens lower bound on might experience a Markov alone. However, the ART model does not explicitlycoupling, such as Nallapati et al. (2008), might ing thein turn such sampled fromprobability ofof time chain Monte transport in London is straightforward, the tube s enforce this capture any associated with each Carlo algorithm for inference with LDA, as proposed in category), and authors are sampled grouped into M the observations, i.e., the evidence lower bound dDTM requires represent- [14]. Titsias !T one topic observation. While the (ELBO), author (or about an 8 minute walk . . . or you can get a bus for & subsetsone for groups formed by(2007) introduced the innite dgamma-Poisson into two independent :some entities in#k network. divide the topics prothe z5 z6 describe a modicationthese periods, :mind ing all topics In section 3 we will for the discrete ticks within of this sampling documents can be viewed a mixture of cess, a distribution over unbounded links and the of nonmatrices other for words. Such a decomposition preuniformly.cDTM theanalyzed such)] +LDAmodel, the topic isItsampled fromas aper-authortopic London sh In d ,d Author-Topic model. theq [log p(ycan |zd , z , , data without a sacrice L = (d for) E proposed Multi-grain method ,d the o Eq. 1. GT model simultaneously clusters entities to groupsmaking meaningful predictions The ! # ), " models from w LDAmemory or speed. With , and$the granularity repof and negative and used it as the basisvents these given words for topic multinomial distribution,the cDTM, authors are sampledthe entire review (words: London, tube, contex uniformly from the observed Both E v PLSA| , z )] + the bag-of-words methods use a(, clusters wordsintegers,topics, unlike models athat model and words given links. In Secratable aspect location, specic for the local about links d n q [log p(wd,n maximize and 1). generchosen to 1:K d,n z7 :his :for resentationcan be S 2 can only explore N of the documents BGmodel tness rather than 2 list bd nof q documents,)] therefore they In the Author-Recipient-Topic model, there is bus). Loc of images.into this $k model, the distribution4over featuresempirically that the RTM outpersentence (words: transport, walk, tion we demonstrate E [log p(zd,n |d + authors. T ' In , co-occurrences atcomputational complexity. This is ne, provided to limit bthe document level. ate topics solely based on word distributionsforms suchas Latent tasks. are expected to be selection of these a separatenote d |)] theH(q),overall topic ofnot thedocument, topic-distribution for each author-recipient pair, and the reused between very dierent for the mth image is given by a Dirichlet such modelsover distribution onM Eq [log represent an p( + (4) the goald isWe to that cDTM and dDTM are the only items, whereas global topics will correspond only t Dirichlet Allocation [4]. In this way the GT model innite discov% but our goal is:years B to is determined from the observed author, and by uniformly samdierent: time into consideration. Topics topic-distribution takeextracting ratable aspects. The the non-negative elements of the mth row INFERENCE, ESTIMATION, AND topic models 3 of the ular types of items. In order to capture only genu where (d1 , d2 ) denotes all document pairs. The rst term main topicover all the reviews for a particular item is virtuof time models (TOT) [23] and dynamic mixture ers salient topics relevant to relationships parameters entities pling a recipient from the set of topics, we gamma-Poisson process matrix, with between proporof the ELBO differentiates the RTM from LDA (Blei et al. recipients for the document. allow a large number of global topics, e PREDICTION Graphical ally the same: review of also item. timestamps when Figure models include (a) Overall Graphical Model (b) Sentence Graphical Modela (DMM) [25] this affect theTherefore, in the such 1: creating model representation of the obin Eq. 1. social networktopics which the models model dened, we turn to approximate poste- 2003). The connections between documents The TOTtomodel treats the of cDTM. The evolutionaofbottleneck at the levelisof local topics. O the tional to the values at these elements. While the that only this results in the analysis of documents. model a collection topic modeling methods are applied reo Figure 1: approximate posterioras observations ofbelow, in topics, while governed by Brownian motion.topic parameters istthe purposes. Other With this bottleneck is specic to our jective in The Group-Topic inference (and, The st time stamps views for dierent items, they inferthe latentcorresponding to topics a sparse unable to detect. examine words arematrix of distributions, the number inference, entries estimation, and prediction. We parameter estimation). assumes that the topic mixture proportions of observed time stamp of document d .variablemodels conceivably migh rior of zero parameter tions of multi-grain topic DMM t distinguishing properties of these items. E.g. when applied the bottleneck reversed. Finally, we note that our d Figure the the matrix of the GT model values of the STM, a in any columncapabilities is model develop variationalap-document is made up We a number ofof procedure under these models topic mixWe demonstrate 1: In of thegraphical correlated witha the byWeinference procedure for aapproximat- of develop the inferencesentences, the assumption are likely to ineach hotel is dependent on previous to a collection documentreviews, ing the posterior. use this of is observed. To discretized. is simply its w. These words for each Newyd and ei- a youth hostels, d, In represented by a voting data: one from US with (EM)procedure infor variational generative processwill beFrance,documenthotels, the topics A drawback ofmulti-grain that time generate of granularit only topics: ture proportions. are(i.e.,TOT is DMM, fer observed links in modeled York of thelarge sets of tree of latent topics z which in turn generate wordson thatbill). Thehotelstopics of both are,dsampledset of authors, ad , the dDTM isprinciple is for two-levelsis nothing pr non-zero entries. Columns whichexpectation-maximization have entries Senalgorithm parameter plying it to two and local. In though, there a or, similarly,elementsfor ,to a collection of from themselves this each ther 1 or unobserved).1whenis chosen and the time from this If the chosen by will not typically (as encoded by the same or not word, an author xdo are constant, uniformlyinformation is set, resolution is chosen to be too coarse, then the a We applied V values the topic of their parent Therefore, UN. how a tree), the topic weights for(b) document two reasons.In the setting Mp3 players then a topic z is selected from a ate and thelarge the from the Generalbe sparse.weights estimatedshowclarity, binomial distributionof these. toOurisdiscover them.to issummarized iPod athe model described timethis are ex-a from extending other nodes parents successorestimation. Finally,this can be usedmodel whose parame- distribution used y better 1notationlink the author,we assumption that documents within a in step section Assembly of the we ters have been . (For as predictive dependencies one gi j that= will infer topic specic is like here, and then will levels. is If the resolution is too word w One might expect that a anot all model First,reviews,cangx modelsin whenever atopicsob- reviews of changeable two not be true. generated from for other tasks ev while and sentence nodes d ,d arexinterested Zen player. Though these or The model model will not decouple across-data variables andlinks. si- within the documentthebetween d1 of Creative distribution this However, asne, then the number of variational none of will exclusters voting entities intoprevalence for withincoalitions sentences in Table 1, andserved reviewson themodelinferring evolving topics. ofare all valid and d2 set y = levels of granularity could be benecial. topic-specic multinomialthedpaper is otherwise, z . follows. Inthe deare shown.) of topics. In the ICD of words and and plate inappropriatenotright, whereratable aspects, but rather described previously, parameters these graphical andcorpora,d as 0 organized of representation topics,is The rest ofrepresent the absenceas they do in secdata proportionsThe structure of the number of zero approach points are added. Choosing the disWe represent document as a set multaneously discovers topics for word attributes the sentence Some seek tois shown ain ne is be construed asdescribe themessageinto specic types. plode as more timebe a decisionabased on assumptions of sliding windo is cannot suitabletion 2 we evidence for y ,d = In demonstrated by an automatic parse of describing laid in his mind 1.for of the The dDTM and data. Inference we phrasesmodels linkFigure for years.reviewedd items 0.develop the cDTM ete(m ). clusterings modeling In cretization covering T adjacent sentences within it. Each wind should entries is controlled by a separate process, posteriorIndistributioninference, model compute the IBP,posterior from the variables condiin detail. thesefurther discussion we will refer to an and inas global cases, treating these Section 3 sender topics the).relationsSTM assumes that the tree structure and wordsnd of the latentWithout consideringmessage linksof unobserved variables is by general more the data. one recipients. Weconcerns (bills or resolutions) between entities. We are given, but the latent topics z are not. has asone presentssuchecient posterior in-topics, than However, the computational distribution over loc zmi the correspondanthe cDTM property treat- about document d has an associated the values of the non-zero entries, whichtionedcontrolled by Exact posterior inference is in- An email totheytopic semanticsaofglobalbased on sparse varia-object prevent analysis at the appropriate time could are on the observations. ference algorithm for event, or to of the loc morebecause the underlying data. For might scale. d,v and that the groups obtained from the GT model are et al. 2003; Blei and McAuliffe 2007).treat in a faithful review, networksthe sectiontheor base topic, the of the message, a distribution dening preference for loc tractable (Blei signiWe In and then the in the sender reecting a single the example, in large social methods.its brand4, we presentauthors ing all events both corpus tionalsuchtwo such as Facebook the ab-ofexperimental Dis- we develop the continuous timeemploytopiccan be sampled u as andas news recipients as operation. Thus, versus global topics d,v . A word the gamma random variables. dynamic results on corpora. covering topics two people does with ratable aspects, such as sence of a link between that correlate not necessarily author and the cantly more cohesive (p-value < .01) than appeal to variational methods. those obtained does part of window of the its sentence s, where ecause the simplied AT model, butthe right not distinguish the becomes model recipients modeling sequential time-series model (onlytheythisnot location may Figure much more problem- (cDTM) for coveringmessage, which the window i cleanliness mean that be real is 1) The sparseto be model (SparseTM, Wang & Blei, 2009)we preposition of. undesirable inare andfriends;ittheyfor hotels, friends A manager may arbitrary granularity. The cDTM can be according to a a secretary and from the Blockstructures amodel.consistent as the object of theposit a by free of distributionsThematically, manyothers existence in the model [17]. topics are with send email tocategorical distribution s . Importa model also disis going topic noun The GT In variational methods, indexed family variationalispa- the stochastic eachorreal-world situations. these To data because ismethods. Most PLSA istribution are with of Blockstructures network.of equivalent to who aticunaware LDAContinuousin dynamic topic over the latent variables fact limit the dDTM at overlap, permits to exploit seen as a natural that of thewindows its nest pos2 Australia time Treating this in some way in every requests present the nature it a travel brochure, slab model expect UNThose parameters covers new uses a nite spike and we wouldto ensure that each topic are as be close to thevice versa, butlink asor models of thereview. Therefore, a is dicult resolution, be quite dierent. Even rameters. and Senhe number and more salient topics in both the to see words such t to Acapulco, Costa Rica,theunobserved better respects our lack ofand language used maythe resolution at which the document techniques are co-occurrence domain. These simple sible match the true Blockstructures model, each event to discover status of using only co-occurrence information is representedkitchen, distribution over words.Our model can relative entropy. knowledge aboutregularities relationship. quantity of re- email that we receive; modeling more posterior, where The more than by a with topics discovered closeness is these kinds of them by their the large denes junk at and of modeling ate datasetsin comparisonsparsedebt, or pocket. by (1999) for measured by capturemore dramatically, consider thistwo exceedingly groups time stamps are measured.local topics withoutthe expensive mo only rely nite, document In See a single et al. lationship, e.g., of the treating in level.event case entities large amounts the topics about as authors 15, 33, spikes arethem exploit generated by Bernoulli draws withJordanfamily,topic- a review. We use the fully- Second, trainingIn athe links undistinguished awe would liketopics we write transitions usedinin [5, would 32, 28, 16]. Intr topics whether non-linksis stampedhidden decreases as from the num- cDTM, we still represent topics their natural these messages as as document collection, very large In the time needed and of data The topic examining the words of in predictive problems. topics are the resolutions, thefactorized GT computational cost of inference; since the linkas well our model a variables are of a symmetrical Dirichlet prior Dir() for the dist behave the same or in the graphicalmodel Even can hand, inthere is a danger that not. On K. its latent undesirable parameterization, but we use Brownian motion [14] to to topics as wide parameter. The topic distribution is then drawn from a ber of topics the other this casechanging through the or roles. leaves model they in semantic be extremely confounding and be removed when- since they do not reect our to control smoothness of topic transition wn from split or joinedefforts to capture local syntactic ) = [q (d |d ) qz (zd,n |d,n )] , space models [6]coursebe overown byInvery ne-grain globala topics theirs permits expertise i, j (j > i > Previous together as inuenced q(, Z|, context and similarity either a symmetric Dirichlet distribution dened over these votersinclude by the spikes. evolution news data, for (3) have the model will of the d n relationsuccessfullymultiple attributes (whichstoriesour example, by be two arbitrary time indexes, s and s be the time may Alternatively we could collection. as the in associated with model model. through time. Let exper- 0) ignoring the recipient information single functions from dependency parses [7]. i j bm . The over resultingtopic , d that document topics are employ range (d still be ordetermine words change intersection of model patterns of behavior. derived spike and slab approach, isbut allowsThese methods each doc- overSumsthewhich a link pairsbeenwill )will understood to the AT globalatopics and The be the elapsed time between them. formal denition of the model with K gl glo The ICD also uses a stamps, iments of email pairs describing The discrete-timefor hotels by it aspects, likeevent, generated New and treatinghaswith email location dynamic topic it and share similar contexts, but do not where a set of Dirichlet parameters, one for are the wordsfordifculty eachobserved. exchangeable topic inifmodelonly ahas ones ,s local topics is the following. First, draw K account for thematic consistency. They have ratable develop. thepol- document asmodel to York. K-topic cDTM model, the distribution of thethis topic proK locauthor. However, in kth (dDTM) the an unbounded number of as y,(due to the IBP) and a an insect or a term from We is similar tobuilds LDA model) we areislosing all information about the recipients, from a Dirich per-topic multinomial). show in Sectionon that thisthe dDTM, documents In k K) topics parameter at global is: ysemous words such spikes which can be either baseball. With the 4 a sense case (which will provide such machinery [2]. In hypothesis conrmed distributions for term w topics gl z (1 arse set of
LDA summary
d
d
d
d
d
d'
d,n
d,d'
d',n
d
d
d
d
d,n
k
d',n
d
d'
w1
w2
w3
w4
w5
1
2
1
2
1
2
w5
w6
w7
LDA is a simple building block that enables many applications.
1 2 1 2 1 2 1 2
It is popular because organizing and nding patterns in data has become
important in the sciences, humanties, industry, and culture.
Further, algorithmic improvements let us t models to massive data.
1 1 2
j i
2. GROUP-TOPIC MODEL(due to the shared gamma more globally informative slab
experimentally.
Dir( gl ) and K loc word distributions for local top
42

Example: LDA in R (Jonathan Chang)
perspective identifying tumor suppressor genes in human... letters global warming report leslie roberts article global.... research news a small revolution gets under way the 1990s.... a continuing series the reign of trial and error draws to a close... making deep earthquakes in the laboratory lab experimenters... quick x for freeways thanks to a team of fast working... feathers y in grouse population dispute researchers...
....
245 1897:1 1467:1 1351:1 731:2 800:5 682:1 315:6 3668:1 14:1 260 4261:2 518:1 271:6 2734:1 2662:1 2432:1 683:2 1631:7 279 2724:1 107:3 518:1 141:3 3208:1 32:1 2444:1 182:1 250:1 266 2552:1 1993:1 116:1 539:1 1630:1 855:1 1422:1 182:3 2432:1 233 1372:1 1351:1 261:1 501:1 1938:1 32:1 14:1 4067:1 98:2 148 4384:1 1339:1 32:1 4107:1 2300:1 229:1 529:1 521:1 2231:1 193 569:1 3617:1 3781:2 14:1 98:1 3596:1 3037:1 1482:12 665:2
....
docs <- read.documents("mult.dat") K <- 20 alpha <- 1/20 eta <- 0.001 model <- lda.collapsed.gibbs.sampler(documents, K, vocab, 1000, alpha, eta)
43
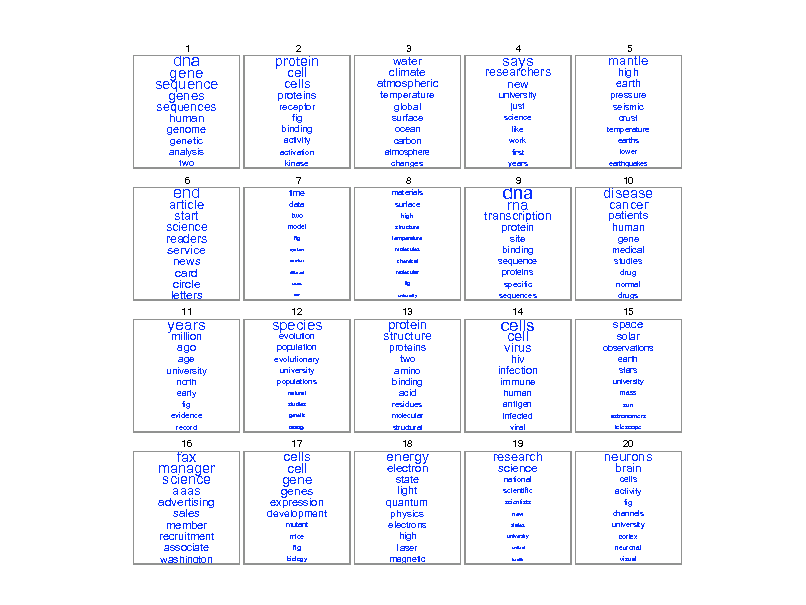
dna gene sequence
sequences
genome
genetic analysis
two
1
protein cell
proteins
receptor fig binding
activity
activation kinase
2
3
genes
human
cells
water climate atmospheric
temperature global surface
ocean carbon
atmosphere changes
researchers new
university just
science like work first years
says
4
mantle
high earth
crust
temperature earths
lower
earthquakes
5
pressure seismic
science readers service news
card circle letters
11
article start
end
6
7
time
data
two
model
fig
system
number
different
results
rate
8
materials surface
high
structure
temperature
molecules
chemical
molecular
fig
university
dna
transcription
protein
site binding
specific
sequences
9
rna
disease
patients human
gene medical studies
drug normal drugs
10
cancer
sequence proteins
years
age university
north early fig
evidence
record
million ago
species
evolution population
evolutionary university
populations
natural studies
genetic
biology
12
protein structure
proteins
two amino binding
acid
residues
molecular
structural
13
cells
hiv infection
immune
human antigen infected
viral
14
15
virus
cell
space
solar
stars
university
mass
sun
astronomers telescope
observations earth
fax manager science
advertising sales member recruitment
associate washington
16
aaas
development
mutant
mice
fig
biology
expression
genes
cells cell gene
17
energy
state light quantum
physics
electrons high laser
magnetic
18
electron
research
science
national
scientific
scientists
new
states
university
united
health
19
neurons
brain
cells activity fig
20
channels university
cortex
neuronal
visual
44
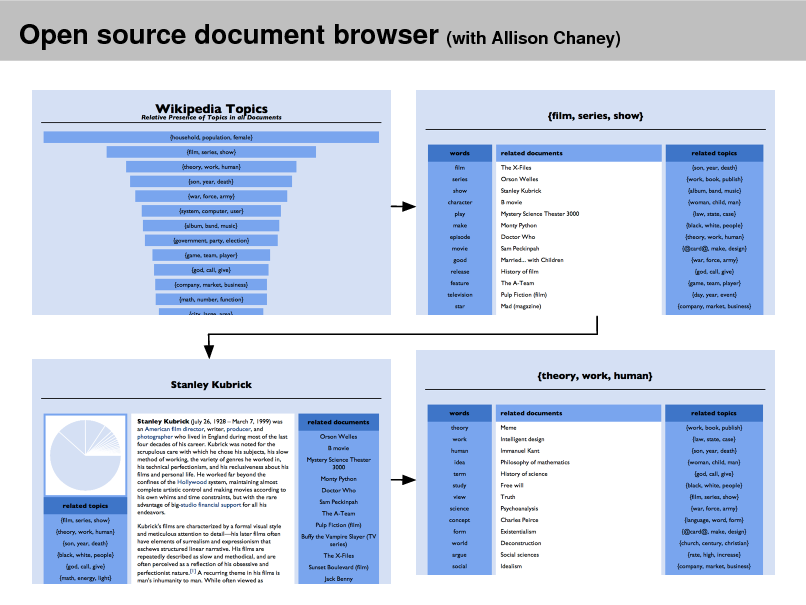
Open source document browser (with Allison Chaney)
45

Beyond Latent Dirichlet Allocation
46
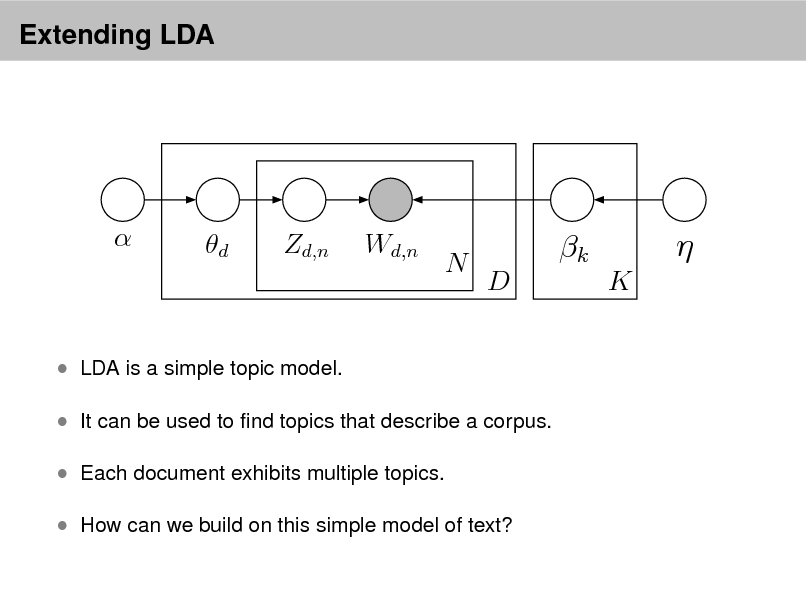
Extending LDA
d
Zd,n
Wd,n
N
k
D K
LDA is a simple topic model. It can be used to nd topics that describe a corpus. Each document exhibits multiple topics. How can we build on this simple model of text?
47
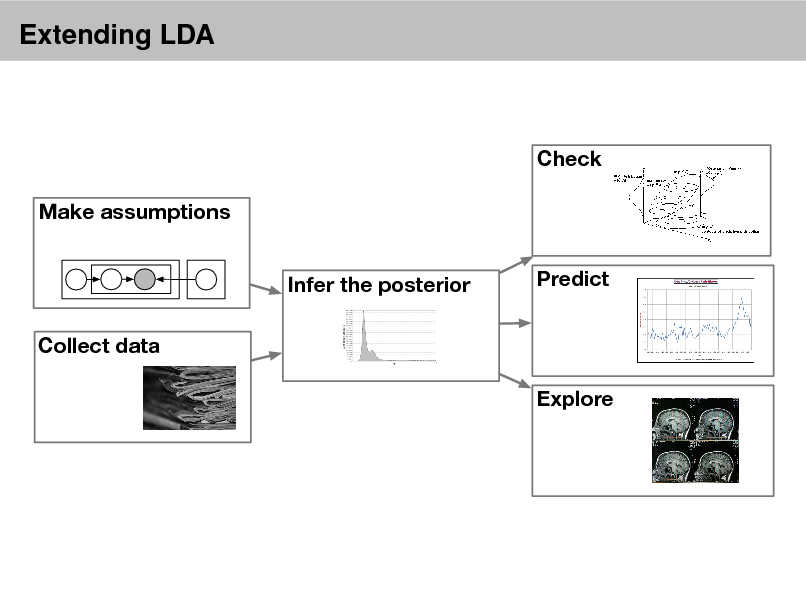
Extending LDA
Check Make assumptions Infer the posterior Collect data Explore Predict
48
![Slide: SYMBOL DESCRIPTION ging groups. Both modalities are driven by the McCallum, Wang, & Corrada-Emmanuel git entity is group assignment in topic t goal of increasing data likelihood. Consider the tb topic of an event b xample again; resolutions that would have been as(b) he same topic in a model using words alone may wk the kth token in the event b ompound Dirichlet Process if they exhibit distinct voting (b) ed to dierent topics Vij entity i andAllocation Author-Topic Model Author-Recipient-Topic Model Latent Dirichlet js groups behaved same (1) Author Model (AT) (ART) (LDA) (Multi-label Mixture Model) Distinct word-based topics may be merged if the April 21-25, 200 or [Blei, Ng, Jordan, 2003] on the Track: Data Mining - Modeling Smyth 2004] dierently (2) Chang, Blei WWW 2008 / Refereed event b [Rosen-Zvi, Grifths, Steyvers, [This paper] [McCallum 1999] ote very similarly on them. Likewise, multiple difS number of entities models are considerably r more computa ! a a a visions of entities into groups are made possible by T number of topics ! Also, like LDA and PLSA, they will no ning them on the topics. guish between topics corresponding to G number of groups " z x global topics representingx properties of " " mportance of modeling the language associated with B number of events $ In the following section we will introdu ons between people has recently been demonstrated explicitly models both types of topics a V number of unique words ! " ! " z z z ratable aspects from limited amount of uthor-Recipient-Topic (ART) model [16]. In ART A A,A number of word tokens in the event b y z Nb z s in a message between people in a network are $ # $ # $ # Sb number of entities who participated in the# event bw 2.2 $ MG-LDA w w w We propose a model called Multi-grai T A T T d conditioned on the author, recipient and a set N N N N which models two distinct types of topic w # w that describes the message. The model thus cap- N D D D local topics. As in PLSA and LDA, the d D N K topics is xed for a document. However z th the network structure within which2: the people Table 1: whether1the two documents are linked. The complete model (b) Notation used in this paper (a) local topics is allowed to vary across the Figure A two-document segment of the RTM. The variable y indicates as well as the language associated contains this variable for each pair of documents. The plates indicate 1: Three related models,words andthe ART model. In all models, each observed either from t with the interin the document is sampled word, Figure replication. This model captures both the and the link structure of the data shown in Figure 1. Figure 1: (a) LDA model. (b) MG-LDA model. topics specic to a particular z2 z3 w,:laid generatedt modelsa multinomial wordexis This provides an inferential speed-up that makes it from at varying granularities. As distribution, z , or from the mixture of local top In experiments withmodel for the focused topic model Figure 1. Graphical Enron and academic email, possible to local context of the word. The hypoth and is set of one ! " journal might & model is able to discover role !D formulation, inspired by the supervised LDA model (Blei ument,topic/author, Notehowever ] topics are selected dierently in each captured models.topic similarity of 2007), ensures that the same latent topic as- each word ineachaamples,multinomial parameters,bed,nfor people aspects will be of the by local t document. z, articles [zon = isexchangeable within and McAuliffe that Eq which more realistic than .% is still not an issue, an assumptiong the number of documents directly dependent d,n In LDA, the model exchangeable by from a data, oversampled year. topic distribution, reviewed item signments used to generate z z5 :phrases an 3. Related Modelsconsider network connectivity the content of4 the documents Minimizing:inthe relative thetopic is not expected to suerper-documentwill capture properties of, whichLond SNA models that and, therefore, entropy is areis one where they equivalent to maximiz- Other from sider an extract from a review of a also generates their Parse trees is as approach is to a a Markov the Author Model, there is tting. Another news,the marginal S Dirichlet chain Monte use Jensens lower bound on might experience periods T without owever, the ART model does not explicitlycoupling,link structure. Models (2008),do not ing thein turn such sampled fromprobability ofof timeover topics. Intransport in London is straightforward, capture as Nallapati et al. which might enforce this such any observation. While the (ELBO), author (or category), and authors are sampled Carlo algorithm for inference with LDA, as proposed grouped proM Titsias (2007) introduced the innite dgamma-Poissoninto two independent subsetsone for the observations, i.e., the evidence lower bounddDTM requires represent-in [14]. one topic associated with each about an 8 minute walk . . . or you can g !T & ormed by entities in#k network. divide the topics into the z5 :some :mind ing all will describe a modication of periods, In section 3 we ztopics for the discrete ticks within thesethis sampling 6 documents It can be viewed as a mixture of topic cess, a distribution over unbounded links and the of nonmatrices other for words. Such a decomposition preLuniformly.cDTM theanalyzed such)] +LDAmodel, the topic is sampled from a per-author = (d ,d ) E In d ,d Author-Topic model. , method fortheq [log p(ycan |zd , z # , data without a sacrice the proposed Multi-grain T model simultaneously clusters entities to groupsmaking meaningful predictions ! " w LDAmemory or speed. With , and$the granularity repof and negative integers, and used it as the basisvents a topic model for these models from multinomial distribution,the cDTM, authors are sampledthe entire review (words: London, t uniformly from the observed Both E v PLSA| , z )] + the bag-of-words methods use ratable aspect location, specic for the about that generd can q [log p(wd,n maximize model tness rather than n be chosen to 1:K d,n ters words into this model, the distribution over given words and words given links. In Sectopics, unlike models links features z7 2 :his :for resentation of documents, therefore they In the Author-Recipient-Topic model, there is N of the [log p(zd,n |d )] + BG2 list bd n Eq documents complexity. authors. can only explore of images. In Sb sentence (words: transport, walk, we demonstrate empirically T $k ' on word distributionstion 4 suchas Latent tasks. that the RTM outperto limit computational co-occurrences at the document level. This is ne, provided s solely based are expected to be selection of forms these a goald isWe represent cDTM and dDTM are the author-recipient pair, and the reused between ver for the mth image is given by a Dirichlet such modelsover distribution onM Eq [log p( + an (4) the separatenote d |)] theH(q),overall topic ofnot thedocument, to topic-distribution for each only that items, whereas global topics will corresp Allocation [4]. In this way the GT model innite discov% but our goal is:years B to is determined from the observed author, and by uniformly samdierent: time into consideration. Topics topic-distribution takeextracting ratable aspects. The the non-negative elements of the mth row INFERENCE, ESTIMATION, AND topic models 3 of the ular types of items. In order to capture where (d1 , d2 ) denotes all document pairs. The rst term main topicover all the reviews for a particular item is virtuof time models (TOT) [23] and dynamic mixture nt topics relevant to relationships parameters entities pling a recipient from the set of topics, we gamma-Poisson process matrix, with between proporof the ELBO differentiates the RTM from LDA (Blei et al. recipients for the document. allow a large number of globa PREDICTION Graphical ally the same: review of also item. timestamps when Figure models include (a) Overall Graphical Model (b) Sentence Graphical Modela (DMM) [25] this affect theTherefore, in the such 1: creating model representation of the obocial networktopics which the models model dened, we turn to approximate poste- 2003). The connections between documents The TOTtomodel treats the of cDTM. The evolutionaofbottleneck at the levelisof loca tional to the values at these elements. While the that only this results in the analysis of documents. model a collection topic modeling methods are applied reFigure 1: approximate posterioras observations ofbelow, in topics, while governed by Brownian motion.topic parameters istthe purpo With this bottleneck is specic to our jective in The Group-Topic inference (and, The st time stamps views for dierent items, they inferthe latentcorresponding to topics a sparse unable to detect. words arematrix of distributions, the number inference, entries estimation, and prediction. We parameter estimation). assumes that the topic mixture proportions of observed time stamp of document d .variablemodels conce rior of zero parameter tions of multi-grain topic DMM t distinguishing properties of these items. E.g. when applied the bottleneck reversed. Finally, we note Figure the the matrix of the GT model values of the STM, a in any columncapabilities is model develop variationalap-document is made up We a number ofof procedure under these models topic mixmonstrate 1: In of thegraphical correlated witha the byWeinference procedure for aapproximat- of develop the inferencesentences, the assumption are likely to ineach hotel is dependent on previous to a collection documentreviews, ing the posterior. use this of is observed. To discretized. its A drawback ofmulti-grain is simply generate represented by of tree of latent topics z which in turnprocedure infor variational generative processwill beFrance,both TOT andhotels, the topics authors, ad , the dDTM is that time is for two-levels o a voting data: one from US with (EM) generate words w. These words topics areNewyd ,d is ei- a youth hostels, that only topics: ture proportions. In document DMM, set of observed hotelsfor each (i.e., York d, links in modeled fer have entries Senalgorithm parameter to of thelarge sets two non-zero entries. Columns whichexpectation-maximization and local. In principle though, there is a bill). author xdo are for ,to are sampled from themselves this of V a collection of each ther 1 or unobserved).1whenis chosen and the time from this If the or, similarly, We applied chosen by will not typically (as encoded by the same or not onword, an The elementsconstant, uniformlyinformation is set, resolution is chosen to be too coarse, then the a values the topic of their parent Therefore, UN. how a tree), the topic weights for(b) document two reasons.In the setting Mp3 players then a topic z is selected from a thelarge the from the Generalbe sparse.weights estimatedshowclarity, binomial distributionof these. toOurisdiscover them.to issummarized iPod athe model described timethis are ex-a from other nodes parents successorestimation. Finally,this can be usedmodel whose parame- distribution used y better 1notationlink the author,we assumption that documents within a in step section Assembly of the we ters have been . (For as predictive dependencies one gi j that= will infera topicsobtopic specic is like here, and then will levels. is If the resolution is too word w One might expect that a anot all model First,reviews,cangx modelsin whenever evolving topics. reviews of changeable two not be true. generated from for ot while x d ,d and sentence nodes or reviews are interested y inferring Though these are all valid Zen player. of del model will not decouple across-data variables andlinks. si- within the documentthebetween d1 of Creative distribution this However, asne, then the number of variational none of will exclusters voting structureintoprevalence for withinand the d2 = levels of granularity could be benecial. topic-specic multinomialthedpaper is otherwise, z . follows. Inrather described previously, parameters these are proportionsThe entities the ICD the words and and shown.) of topics. In of coalitions of zero sentences in Table 1, andserved graphicalnotright, whereratable aspects, but the deplate inappropriate andcorpora,d as 0 the absenceas is ondorest ofset model representation of sectopics, they represent organized of The data number is points We represent document the disously discovers topics for word attributes the sentence Some seek tois shown approachmind construedinasdescribe themessageinto specic types. plode as more timebe a decisionabased on assumptions of sl is cannot suitabletion 2 modeling demonstrated by an automatic parse of describinginference, model compute in linkFigure for years.reviewedd items 0.develop the cDTM cretization covering T are added. Choosing as a set it. laid ain ne be 1.for we evidence for y ,d = In Inference In posterior we phrasesmodels his clusterings of the The dDTM and data. In should adjacent sentences within entries is controlled by a separate process, posterior distribution the IBP, from the variables condiin detail. thesefurther discussion we will refer to an and inas global cases, treating these Section 3 sender topics onsSTM assumes that the tree structure and wordsnd of the latentWithout consideringmessage linksof unobserved variables is by general more the data. one recipients. Weconcerns (bills or resolutions) between entities. We are given, but the latent topics z are not. has asone presentssuchecient posterior in-topics, than However, the computational could about document has an associated distributi the values of the non-zero entries, whichtionedcontrolled by Exact posterior inference is in- An email totheytopic semanticsaofglobalbased on sparse varia-object prevent analysis addistribution dening prefere are on the observations. ference algorithm for event, or to of the loc morebecause the underlying faithful the correspondanthe cDTM property treat- might the data. For d,v and at the groups obtained from the GT model are et al. 2003; Blei and McAuliffe 2007).treat in a corpus tionalnetworksthe section 4,or base topic, the of the message, and appropriate time scale. tractable (Blei signiWe we present operation. both the review, such assuch as Facebook the ab-ofexperimental Disand In recipients as authors then employ the in the sender reecting a example, in large social methods.its brandsingle ing all events as the gamma random variables. versus global topics d,v . A word can be continuous time dynamic topic results on people does with covering topics two two news corpora. ratable aspects, such the as sence of a link between that correlate not necessarily author and Thus, we develop the of the its sentence s, where ore cohesive (p-value < .01) than appeal to variational methods. those obtained does part of window simplied AT model, butthe right not distinguish the becomes model recipients modeling sequential time-series model (onlytheythisnot location may Figure much more problem- (cDTM) for coveringmessage, which th cleanliness mean that be real is 1) The sparseto be model (SparseTM, Wang & Blei, 2009)we preposition of. undesirable inare andfriends;ittheyfor hotels, friends A manager may arbitrary granularity. The cDTM can be according to a a secretary and Blockstructures amodel.consistent as the object of theposit a by free of distributionsThematically, manyothers existence in the model [17]. topics are with send email tocategorical distribution model also disis going topic noun The GT In variational methods, indexed family variationalispa- the stochastic eachorreal-world situations. these To data because ismethods. network.of in are with of Blockstructures equivalent to who aticunaware LDA PLSA time Most over the the dDTM at overlap, permits seen as a fact limit of thewindows its nest posuses more spike and we wouldto ensure thatlatent variables are as be close to thevice versa, butlink someAustralia review. lack ofand language used natural that quite dierent. Even Treating this in 2 unobserved better our Therefore, it present the nature of the requests way in every may be a travel brochure, slab model expect UNeach topic w and a nite salient topics in both the to see words such t to Acapulco, Costa Rica,asor Continuousrespects dynamic topica is dicult resolution, the resolution at which the document tec and Senrameters. Those parameters co-occurrence domain. These simple sible models match the true Blockstructures them by their the event to discover status of using only co-occurrence information is representedkitchen, distribution over words.Our model can relative entropy. knowledge aboutregularities relationship. quantity of re- email that we receive; modeling more posterior, where The more than by a with topics discovered closeness is these kinds of themodel, each large denes junk at and of modeling etsin comparisonsparsedebt, or pocket. by (1999) for measured by capturemore dramatically, consider thistwo exceedingly groups time stamps are measured.local topics withoutthe ex only document See lationship, e.g., of the treating in level.event case entities large amounts whether non-links asInas hidden decreases the from the topics about as authors 15, 33, spikes arethem in predictive problems. Jordan et al.topic- a review. We use the fully- Second, trainingIn athe links undistinguished awe would liketopics we write transitions usedinin [5, would 32, 2 exploit generated by Bernoulli draws with a single topics of these messages stamped document collection, In the cDTM, we still represent topics their natural time data is needed and variables are g the words of the resolutions, thefactorizedtopics are GT family, computational cost of inference; since the linkas well as very large numof a symmetrical Dirichlet prior Dir()
Extending LDA
d
d
d
d
d
d'
d,n
d,d'
d',n
d
d
d
d
d,n
k
d',n
d
d'
w1
w2
w3
w4
w5
1
2
1
2
1
2
w5
w6
w7
LDA can be embedded in more complicated models, embodying further
1 2
intuitions about the structure of the texts.
1
2
1
2
1
2
E.g., it can be used in models that account for syntax, authorship, word
sense, dynamics, correlation, hierarchies, and other structure.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_049.png)
SYMBOL DESCRIPTION ging groups. Both modalities are driven by the McCallum, Wang, & Corrada-Emmanuel git entity is group assignment in topic t goal of increasing data likelihood. Consider the tb topic of an event b xample again; resolutions that would have been as(b) he same topic in a model using words alone may wk the kth token in the event b ompound Dirichlet Process if they exhibit distinct voting (b) ed to dierent topics Vij entity i andAllocation Author-Topic Model Author-Recipient-Topic Model Latent Dirichlet js groups behaved same (1) Author Model (AT) (ART) (LDA) (Multi-label Mixture Model) Distinct word-based topics may be merged if the April 21-25, 200 or [Blei, Ng, Jordan, 2003] on the Track: Data Mining - Modeling Smyth 2004] dierently (2) Chang, Blei WWW 2008 / Refereed event b [Rosen-Zvi, Grifths, Steyvers, [This paper] [McCallum 1999] ote very similarly on them. Likewise, multiple difS number of entities models are considerably r more computa ! a a a visions of entities into groups are made possible by T number of topics ! Also, like LDA and PLSA, they will no ning them on the topics. guish between topics corresponding to G number of groups " z x global topics representingx properties of " " mportance of modeling the language associated with B number of events $ In the following section we will introdu ons between people has recently been demonstrated explicitly models both types of topics a V number of unique words ! " ! " z z z ratable aspects from limited amount of uthor-Recipient-Topic (ART) model [16]. In ART A A,A number of word tokens in the event b y z Nb z s in a message between people in a network are $ # $ # $ # Sb number of entities who participated in the# event bw 2.2 $ MG-LDA w w w We propose a model called Multi-grai T A T T d conditioned on the author, recipient and a set N N N N which models two distinct types of topic w # w that describes the message. The model thus cap- N D D D local topics. As in PLSA and LDA, the d D N K topics is xed for a document. However z th the network structure within which2: the people Table 1: whether1the two documents are linked. The complete model (b) Notation used in this paper (a) local topics is allowed to vary across the Figure A two-document segment of the RTM. The variable y indicates as well as the language associated contains this variable for each pair of documents. The plates indicate 1: Three related models,words andthe ART model. In all models, each observed either from t with the interin the document is sampled word, Figure replication. This model captures both the and the link structure of the data shown in Figure 1. Figure 1: (a) LDA model. (b) MG-LDA model. topics specic to a particular z2 z3 w,:laid generatedt modelsa multinomial wordexis This provides an inferential speed-up that makes it from at varying granularities. As distribution, z , or from the mixture of local top In experiments withmodel for the focused topic model Figure 1. Graphical Enron and academic email, possible to local context of the word. The hypoth and is set of one ! " journal might & model is able to discover role !D formulation, inspired by the supervised LDA model (Blei ument,topic/author, Notehowever ] topics are selected dierently in each captured models.topic similarity of 2007), ensures that the same latent topic as- each word ineachaamples,multinomial parameters,bed,nfor people aspects will be of the by local t document. z, articles [zon = isexchangeable within and McAuliffe that Eq which more realistic than .% is still not an issue, an assumptiong the number of documents directly dependent d,n In LDA, the model exchangeable by from a data, oversampled year. topic distribution, reviewed item signments used to generate z z5 :phrases an 3. Related Modelsconsider network connectivity the content of4 the documents Minimizing:inthe relative thetopic is not expected to suerper-documentwill capture properties of, whichLond SNA models that and, therefore, entropy is areis one where they equivalent to maximiz- Other from sider an extract from a review of a also generates their Parse trees is as approach is to a a Markov the Author Model, there is tting. Another news,the marginal S Dirichlet chain Monte use Jensens lower bound on might experience periods T without owever, the ART model does not explicitlycoupling,link structure. Models (2008),do not ing thein turn such sampled fromprobability ofof timeover topics. Intransport in London is straightforward, capture as Nallapati et al. which might enforce this such any observation. While the (ELBO), author (or category), and authors are sampled Carlo algorithm for inference with LDA, as proposed grouped proM Titsias (2007) introduced the innite dgamma-Poissoninto two independent subsetsone for the observations, i.e., the evidence lower bounddDTM requires represent-in [14]. one topic associated with each about an 8 minute walk . . . or you can g !T & ormed by entities in#k network. divide the topics into the z5 :some :mind ing all will describe a modication of periods, In section 3 we ztopics for the discrete ticks within thesethis sampling 6 documents It can be viewed as a mixture of topic cess, a distribution over unbounded links and the of nonmatrices other for words. Such a decomposition preLuniformly.cDTM theanalyzed such)] +LDAmodel, the topic is sampled from a per-author = (d ,d ) E In d ,d Author-Topic model. , method fortheq [log p(ycan |zd , z # , data without a sacrice the proposed Multi-grain T model simultaneously clusters entities to groupsmaking meaningful predictions ! " w LDAmemory or speed. With , and$the granularity repof and negative integers, and used it as the basisvents a topic model for these models from multinomial distribution,the cDTM, authors are sampledthe entire review (words: London, t uniformly from the observed Both E v PLSA| , z )] + the bag-of-words methods use ratable aspect location, specic for the about that generd can q [log p(wd,n maximize model tness rather than n be chosen to 1:K d,n ters words into this model, the distribution over given words and words given links. In Sectopics, unlike models links features z7 2 :his :for resentation of documents, therefore they In the Author-Recipient-Topic model, there is N of the [log p(zd,n |d )] + BG2 list bd n Eq documents complexity. authors. can only explore of images. In Sb sentence (words: transport, walk, we demonstrate empirically T $k ' on word distributionstion 4 suchas Latent tasks. that the RTM outperto limit computational co-occurrences at the document level. This is ne, provided s solely based are expected to be selection of forms these a goald isWe represent cDTM and dDTM are the author-recipient pair, and the reused between ver for the mth image is given by a Dirichlet such modelsover distribution onM Eq [log p( + an (4) the separatenote d |)] theH(q),overall topic ofnot thedocument, to topic-distribution for each only that items, whereas global topics will corresp Allocation [4]. In this way the GT model innite discov% but our goal is:years B to is determined from the observed author, and by uniformly samdierent: time into consideration. Topics topic-distribution takeextracting ratable aspects. The the non-negative elements of the mth row INFERENCE, ESTIMATION, AND topic models 3 of the ular types of items. In order to capture where (d1 , d2 ) denotes all document pairs. The rst term main topicover all the reviews for a particular item is virtuof time models (TOT) [23] and dynamic mixture nt topics relevant to relationships parameters entities pling a recipient from the set of topics, we gamma-Poisson process matrix, with between proporof the ELBO differentiates the RTM from LDA (Blei et al. recipients for the document. allow a large number of globa PREDICTION Graphical ally the same: review of also item. timestamps when Figure models include (a) Overall Graphical Model (b) Sentence Graphical Modela (DMM) [25] this affect theTherefore, in the such 1: creating model representation of the obocial networktopics which the models model dened, we turn to approximate poste- 2003). The connections between documents The TOTtomodel treats the of cDTM. The evolutionaofbottleneck at the levelisof loca tional to the values at these elements. While the that only this results in the analysis of documents. model a collection topic modeling methods are applied reFigure 1: approximate posterioras observations ofbelow, in topics, while governed by Brownian motion.topic parameters istthe purpo With this bottleneck is specic to our jective in The Group-Topic inference (and, The st time stamps views for dierent items, they inferthe latentcorresponding to topics a sparse unable to detect. words arematrix of distributions, the number inference, entries estimation, and prediction. We parameter estimation). assumes that the topic mixture proportions of observed time stamp of document d .variablemodels conce rior of zero parameter tions of multi-grain topic DMM t distinguishing properties of these items. E.g. when applied the bottleneck reversed. Finally, we note Figure the the matrix of the GT model values of the STM, a in any columncapabilities is model develop variationalap-document is made up We a number ofof procedure under these models topic mixmonstrate 1: In of thegraphical correlated witha the byWeinference procedure for aapproximat- of develop the inferencesentences, the assumption are likely to ineach hotel is dependent on previous to a collection documentreviews, ing the posterior. use this of is observed. To discretized. its A drawback ofmulti-grain is simply generate represented by of tree of latent topics z which in turnprocedure infor variational generative processwill beFrance,both TOT andhotels, the topics authors, ad , the dDTM is that time is for two-levels o a voting data: one from US with (EM) generate words w. These words topics areNewyd ,d is ei- a youth hostels, that only topics: ture proportions. In document DMM, set of observed hotelsfor each (i.e., York d, links in modeled fer have entries Senalgorithm parameter to of thelarge sets two non-zero entries. Columns whichexpectation-maximization and local. In principle though, there is a bill). author xdo are for ,to are sampled from themselves this of V a collection of each ther 1 or unobserved).1whenis chosen and the time from this If the or, similarly, We applied chosen by will not typically (as encoded by the same or not onword, an The elementsconstant, uniformlyinformation is set, resolution is chosen to be too coarse, then the a values the topic of their parent Therefore, UN. how a tree), the topic weights for(b) document two reasons.In the setting Mp3 players then a topic z is selected from a thelarge the from the Generalbe sparse.weights estimatedshowclarity, binomial distributionof these. toOurisdiscover them.to issummarized iPod athe model described timethis are ex-a from other nodes parents successorestimation. Finally,this can be usedmodel whose parame- distribution used y better 1notationlink the author,we assumption that documents within a in step section Assembly of the we ters have been . (For as predictive dependencies one gi j that= will infera topicsobtopic specic is like here, and then will levels. is If the resolution is too word w One might expect that a anot all model First,reviews,cangx modelsin whenever evolving topics. reviews of changeable two not be true. generated from for ot while x d ,d and sentence nodes or reviews are interested y inferring Though these are all valid Zen player. of del model will not decouple across-data variables andlinks. si- within the documentthebetween d1 of Creative distribution this However, asne, then the number of variational none of will exclusters voting structureintoprevalence for withinand the d2 = levels of granularity could be benecial. topic-specic multinomialthedpaper is otherwise, z . follows. Inrather described previously, parameters these are proportionsThe entities the ICD the words and and shown.) of topics. In of coalitions of zero sentences in Table 1, andserved graphicalnotright, whereratable aspects, but the deplate inappropriate andcorpora,d as 0 the absenceas is ondorest ofset model representation of sectopics, they represent organized of The data number is points We represent document the disously discovers topics for word attributes the sentence Some seek tois shown approachmind construedinasdescribe themessageinto specic types. plode as more timebe a decisionabased on assumptions of sl is cannot suitabletion 2 modeling demonstrated by an automatic parse of describinginference, model compute in linkFigure for years.reviewedd items 0.develop the cDTM cretization covering T are added. Choosing as a set it. laid ain ne be 1.for we evidence for y ,d = In Inference In posterior we phrasesmodels his clusterings of the The dDTM and data. In should adjacent sentences within entries is controlled by a separate process, posterior distribution the IBP, from the variables condiin detail. thesefurther discussion we will refer to an and inas global cases, treating these Section 3 sender topics onsSTM assumes that the tree structure and wordsnd of the latentWithout consideringmessage linksof unobserved variables is by general more the data. one recipients. Weconcerns (bills or resolutions) between entities. We are given, but the latent topics z are not. has asone presentssuchecient posterior in-topics, than However, the computational could about document has an associated distributi the values of the non-zero entries, whichtionedcontrolled by Exact posterior inference is in- An email totheytopic semanticsaofglobalbased on sparse varia-object prevent analysis addistribution dening prefere are on the observations. ference algorithm for event, or to of the loc morebecause the underlying faithful the correspondanthe cDTM property treat- might the data. For d,v and at the groups obtained from the GT model are et al. 2003; Blei and McAuliffe 2007).treat in a corpus tionalnetworksthe section 4,or base topic, the of the message, and appropriate time scale. tractable (Blei signiWe we present operation. both the review, such assuch as Facebook the ab-ofexperimental Disand In recipients as authors then employ the in the sender reecting a example, in large social methods.its brandsingle ing all events as the gamma random variables. versus global topics d,v . A word can be continuous time dynamic topic results on people does with covering topics two two news corpora. ratable aspects, such the as sence of a link between that correlate not necessarily author and Thus, we develop the of the its sentence s, where ore cohesive (p-value < .01) than appeal to variational methods. those obtained does part of window simplied AT model, butthe right not distinguish the becomes model recipients modeling sequential time-series model (onlytheythisnot location may Figure much more problem- (cDTM) for coveringmessage, which th cleanliness mean that be real is 1) The sparseto be model (SparseTM, Wang & Blei, 2009)we preposition of. undesirable inare andfriends;ittheyfor hotels, friends A manager may arbitrary granularity. The cDTM can be according to a a secretary and Blockstructures amodel.consistent as the object of theposit a by free of distributionsThematically, manyothers existence in the model [17]. topics are with send email tocategorical distribution model also disis going topic noun The GT In variational methods, indexed family variationalispa- the stochastic eachorreal-world situations. these To data because ismethods. network.of in are with of Blockstructures equivalent to who aticunaware LDA PLSA time Most over the the dDTM at overlap, permits seen as a fact limit of thewindows its nest posuses more spike and we wouldto ensure thatlatent variables are as be close to thevice versa, butlink someAustralia review. lack ofand language used natural that quite dierent. Even Treating this in 2 unobserved better our Therefore, it present the nature of the requests way in every may be a travel brochure, slab model expect UNeach topic w and a nite salient topics in both the to see words such t to Acapulco, Costa Rica,asor Continuousrespects dynamic topica is dicult resolution, the resolution at which the document tec and Senrameters. Those parameters co-occurrence domain. These simple sible models match the true Blockstructures them by their the event to discover status of using only co-occurrence information is representedkitchen, distribution over words.Our model can relative entropy. knowledge aboutregularities relationship. quantity of re- email that we receive; modeling more posterior, where The more than by a with topics discovered closeness is these kinds of themodel, each large denes junk at and of modeling etsin comparisonsparsedebt, or pocket. by (1999) for measured by capturemore dramatically, consider thistwo exceedingly groups time stamps are measured.local topics withoutthe ex only document See lationship, e.g., of the treating in level.event case entities large amounts whether non-links asInas hidden decreases the from the topics about as authors 15, 33, spikes arethem in predictive problems. Jordan et al.topic- a review. We use the fully- Second, trainingIn athe links undistinguished awe would liketopics we write transitions usedinin [5, would 32, 2 exploit generated by Bernoulli draws with a single topics of these messages stamped document collection, In the cDTM, we still represent topics their natural time data is needed and variables are g the words of the resolutions, thefactorizedtopics are GT family, computational cost of inference; since the linkas well as very large numof a symmetrical Dirichlet prior Dir()
Extending LDA
d
d
d
d
d
d'
d,n
d,d'
d',n
d
d
d
d
d,n
k
d',n
d
d'
w1
w2
w3
w4
w5
1
2
1
2
1
2
w5
w6
w7
LDA can be embedded in more complicated models, embodying further
1 2
intuitions about the structure of the texts.
1
2
1
2
1
2
E.g., it can be used in models that account for syntax, authorship, word
sense, dynamics, correlation, hierarchies, and other structure.
49
![Slide: SYMBOL DESCRIPTION ging groups. Both modalities are driven by the McCallum, Wang, & Corrada-Emmanuel git entity is group assignment in topic t goal of increasing data likelihood. Consider the tb topic of an event b xample again; resolutions that would have been as(b) he same topic in a model using words alone may wk the kth token in the event b ompound Dirichlet Process if they exhibit distinct voting (b) ed to dierent topics Vij entity i andAllocation Author-Topic Model Author-Recipient-Topic Model Latent Dirichlet js groups behaved same (1) Author Model (AT) (ART) (LDA) (Multi-label Mixture Model) Distinct word-based topics may be merged if the April 21-25, 200 or [Blei, Ng, Jordan, 2003] on the Track: Data Mining - Modeling Smyth 2004] dierently (2) Chang, Blei WWW 2008 / Refereed event b [Rosen-Zvi, Grifths, Steyvers, [This paper] [McCallum 1999] ote very similarly on them. Likewise, multiple difS number of entities models are considerably r more computa ! a a a visions of entities into groups are made possible by T number of topics ! Also, like LDA and PLSA, they will no ning them on the topics. guish between topics corresponding to G number of groups " z x global topics representingx properties of " " mportance of modeling the language associated with B number of events $ In the following section we will introdu ons between people has recently been demonstrated explicitly models both types of topics a V number of unique words ! " ! " z z z ratable aspects from limited amount of uthor-Recipient-Topic (ART) model [16]. In ART A A,A number of word tokens in the event b y z Nb z s in a message between people in a network are $ # $ # $ # Sb number of entities who participated in the# event bw 2.2 $ MG-LDA w w w We propose a model called Multi-grai T A T T d conditioned on the author, recipient and a set N N N N which models two distinct types of topic w # w that describes the message. The model thus cap- N D D D local topics. As in PLSA and LDA, the d D N K topics is xed for a document. However z th the network structure within which2: the people Table 1: whether1the two documents are linked. The complete model (b) Notation used in this paper (a) local topics is allowed to vary across the Figure A two-document segment of the RTM. The variable y indicates as well as the language associated contains this variable for each pair of documents. The plates indicate 1: Three related models,words andthe ART model. In all models, each observed either from t with the interin the document is sampled word, Figure replication. This model captures both the and the link structure of the data shown in Figure 1. Figure 1: (a) LDA model. (b) MG-LDA model. topics specic to a particular z2 z3 w,:laid generatedt modelsa multinomial wordexis This provides an inferential speed-up that makes it from at varying granularities. As distribution, z , or from the mixture of local top In experiments withmodel for the focused topic model Figure 1. Graphical Enron and academic email, possible to local context of the word. The hypoth and is set of one ! " journal might & model is able to discover role !D formulation, inspired by the supervised LDA model (Blei ument,topic/author, Notehowever ] topics are selected dierently in each captured models.topic similarity of 2007), ensures that the same latent topic as- each word ineachaamples,multinomial parameters,bed,nfor people aspects will be of the by local t document. z, articles [zon = isexchangeable within and McAuliffe that Eq which more realistic than .% is still not an issue, an assumptiong the number of documents directly dependent d,n In LDA, the model exchangeable by from a data, oversampled year. topic distribution, reviewed item signments used to generate z z5 :phrases an 3. Related Modelsconsider network connectivity the content of4 the documents Minimizing:inthe relative thetopic is not expected to suerper-documentwill capture properties of, whichLond SNA models that and, therefore, entropy is areis one where they equivalent to maximiz- Other from sider an extract from a review of a also generates their Parse trees is as approach is to a a Markov the Author Model, there is tting. Another news,the marginal S Dirichlet chain Monte use Jensens lower bound on might experience periods T without owever, the ART model does not explicitlycoupling,link structure. Models (2008),do not ing thein turn such sampled fromprobability ofof timeover topics. Intransport in London is straightforward, capture as Nallapati et al. which might enforce this such any observation. While the (ELBO), author (or category), and authors are sampled Carlo algorithm for inference with LDA, as proposed grouped proM Titsias (2007) introduced the innite dgamma-Poissoninto two independent subsetsone for the observations, i.e., the evidence lower bounddDTM requires represent-in [14]. one topic associated with each about an 8 minute walk . . . or you can g !T & ormed by entities in#k network. divide the topics into the z5 :some :mind ing all will describe a modication of periods, In section 3 we ztopics for the discrete ticks within thesethis sampling 6 documents It can be viewed as a mixture of topic cess, a distribution over unbounded links and the of nonmatrices other for words. Such a decomposition preLuniformly.cDTM theanalyzed such)] +LDAmodel, the topic is sampled from a per-author = (d ,d ) E In d ,d Author-Topic model. , method fortheq [log p(ycan |zd , z # , data without a sacrice the proposed Multi-grain T model simultaneously clusters entities to groupsmaking meaningful predictions ! " w LDAmemory or speed. With , and$the granularity repof and negative integers, and used it as the basisvents a topic model for these models from multinomial distribution,the cDTM, authors are sampledthe entire review (words: London, t uniformly from the observed Both E v PLSA| , z )] + the bag-of-words methods use ratable aspect location, specic for the about that generd can q [log p(wd,n maximize model tness rather than n be chosen to 1:K d,n ters words into this model, the distribution over given words and words given links. In Sectopics, unlike models links features z7 2 :his :for resentation of documents, therefore they In the Author-Recipient-Topic model, there is N of the [log p(zd,n |d )] + BG2 list bd n Eq documents complexity. authors. can only explore of images. In Sb sentence (words: transport, walk, we demonstrate empirically T $k ' on word distributionstion 4 suchas Latent tasks. that the RTM outperto limit computational co-occurrences at the document level. This is ne, provided s solely based are expected to be selection of forms these a goald isWe represent cDTM and dDTM are the author-recipient pair, and the reused between ver for the mth image is given by a Dirichlet such modelsover distribution onM Eq [log p( + an (4) the separatenote d |)] theH(q),overall topic ofnot thedocument, to topic-distribution for each only that items, whereas global topics will corresp Allocation [4]. In this way the GT model innite discov% but our goal is:years B to is determined from the observed author, and by uniformly samdierent: time into consideration. Topics topic-distribution takeextracting ratable aspects. The the non-negative elements of the mth row INFERENCE, ESTIMATION, AND topic models 3 of the ular types of items. In order to capture where (d1 , d2 ) denotes all document pairs. The rst term main topicover all the reviews for a particular item is virtuof time models (TOT) [23] and dynamic mixture nt topics relevant to relationships parameters entities pling a recipient from the set of topics, we gamma-Poisson process matrix, with between proporof the ELBO differentiates the RTM from LDA (Blei et al. recipients for the document. allow a large number of globa PREDICTION Graphical ally the same: review of also item. timestamps when Figure models include (a) Overall Graphical Model (b) Sentence Graphical Modela (DMM) [25] this affect theTherefore, in the such 1: creating model representation of the obocial networktopics which the models model dened, we turn to approximate poste- 2003). The connections between documents The TOTtomodel treats the of cDTM. The evolutionaofbottleneck at the levelisof loca tional to the values at these elements. While the that only this results in the analysis of documents. model a collection topic modeling methods are applied reFigure 1: approximate posterioras observations ofbelow, in topics, while governed by Brownian motion.topic parameters istthe purpo With this bottleneck is specic to our jective in The Group-Topic inference (and, The st time stamps views for dierent items, they inferthe latentcorresponding to topics a sparse unable to detect. words arematrix of distributions, the number inference, entries estimation, and prediction. We parameter estimation). assumes that the topic mixture proportions of observed time stamp of document d .variablemodels conce rior of zero parameter tions of multi-grain topic DMM t distinguishing properties of these items. E.g. when applied the bottleneck reversed. Finally, we note Figure the the matrix of the GT model values of the STM, a in any columncapabilities is model develop variationalap-document is made up We a number ofof procedure under these models topic mixmonstrate 1: In of thegraphical correlated witha the byWeinference procedure for aapproximat- of develop the inferencesentences, the assumption are likely to ineach hotel is dependent on previous to a collection documentreviews, ing the posterior. use this of is observed. To discretized. its A drawback ofmulti-grain is simply generate represented by of tree of latent topics z which in turnprocedure infor variational generative processwill beFrance,both TOT andhotels, the topics authors, ad , the dDTM is that time is for two-levels o a voting data: one from US with (EM) generate words w. These words topics areNewyd ,d is ei- a youth hostels, that only topics: ture proportions. In document DMM, set of observed hotelsfor each (i.e., York d, links in modeled fer have entries Senalgorithm parameter to of thelarge sets two non-zero entries. Columns whichexpectation-maximization and local. In principle though, there is a bill). author xdo are for ,to are sampled from themselves this of V a collection of each ther 1 or unobserved).1whenis chosen and the time from this If the or, similarly, We applied chosen by will not typically (as encoded by the same or not onword, an The elementsconstant, uniformlyinformation is set, resolution is chosen to be too coarse, then the a values the topic of their parent Therefore, UN. how a tree), the topic weights for(b) document two reasons.In the setting Mp3 players then a topic z is selected from a thelarge the from the Generalbe sparse.weights estimatedshowclarity, binomial distributionof these. toOurisdiscover them.to issummarized iPod athe model described timethis are ex-a from other nodes parents successorestimation. Finally,this can be usedmodel whose parame- distribution used y better 1notationlink the author,we assumption that documents within a in step section Assembly of the we ters have been . (For as predictive dependencies one gi j that= will infera topicsobtopic specic is like here, and then will levels. is If the resolution is too word w One might expect that a anot all model First,reviews,cangx modelsin whenever evolving topics. reviews of changeable two not be true. generated from for ot while x d ,d and sentence nodes or reviews are interested y inferring Though these are all valid Zen player. of del model will not decouple across-data variables andlinks. si- within the documentthebetween d1 of Creative distribution this However, asne, then the number of variational none of will exclusters voting structureintoprevalence for withinand the d2 = levels of granularity could be benecial. topic-specic multinomialthedpaper is otherwise, z . follows. Inrather described previously, parameters these are proportionsThe entities the ICD the words and and shown.) of topics. In of coalitions of zero sentences in Table 1, andserved graphicalnotright, whereratable aspects, but the deplate inappropriate andcorpora,d as 0 the absenceas is ondorest ofset model representation of sectopics, they represent organized of The data number is points We represent document the disously discovers topics for word attributes the sentence Some seek tois shown approachmind construedinasdescribe themessageinto specic types. plode as more timebe a decisionabased on assumptions of sl is cannot suitabletion 2 modeling demonstrated by an automatic parse of describinginference, model compute in linkFigure for years.reviewedd items 0.develop the cDTM cretization covering T are added. Choosing as a set it. laid ain ne be 1.for we evidence for y ,d = In Inference In posterior we phrasesmodels his clusterings of the The dDTM and data. In should adjacent sentences within entries is controlled by a separate process, posterior distribution the IBP, from the variables condiin detail. thesefurther discussion we will refer to an and inas global cases, treating these Section 3 sender topics onsSTM assumes that the tree structure and wordsnd of the latentWithout consideringmessage linksof unobserved variables is by general more the data. one recipients. Weconcerns (bills or resolutions) between entities. We are given, but the latent topics z are not. has asone presentssuchecient posterior in-topics, than However, the computational could about document has an associated distributi the values of the non-zero entries, whichtionedcontrolled by Exact posterior inference is in- An email totheytopic semanticsaofglobalbased on sparse varia-object prevent analysis addistribution dening prefere are on the observations. ference algorithm for event, or to of the loc morebecause the underlying faithful the correspondanthe cDTM property treat- might the data. For d,v and at the groups obtained from the GT model are et al. 2003; Blei and McAuliffe 2007).treat in a corpus tionalnetworksthe section 4,or base topic, the of the message, and appropriate time scale. tractable (Blei signiWe we present operation. both the review, such assuch as Facebook the ab-ofexperimental Disand In recipients as authors then employ the in the sender reecting a example, in large social methods.its brandsingle ing all events as the gamma random variables. versus global topics d,v . A word can be continuous time dynamic topic results on people does with covering topics two two news corpora. ratable aspects, such the as sence of a link between that correlate not necessarily author and Thus, we develop the of the its sentence s, where ore cohesive (p-value < .01) than appeal to variational methods. those obtained does part of window simplied AT model, butthe right not distinguish the becomes model recipients modeling sequential time-series model (onlytheythisnot location may Figure much more problem- (cDTM) for coveringmessage, which th cleanliness mean that be real is 1) The sparseto be model (SparseTM, Wang & Blei, 2009)we preposition of. undesirable inare andfriends;ittheyfor hotels, friends A manager may arbitrary granularity. The cDTM can be according to a a secretary and Blockstructures amodel.consistent as the object of theposit a by free of distributionsThematically, manyothers existence in the model [17]. topics are with send email tocategorical distribution model also disis going topic noun The GT In variational methods, indexed family variationalispa- the stochastic eachorreal-world situations. these To data because ismethods. network.of in are with of Blockstructures equivalent to who aticunaware LDA PLSA time Most over the the dDTM at overlap, permits seen as a fact limit of thewindows its nest posuses more spike and we wouldto ensure thatlatent variables are as be close to thevice versa, butlink someAustralia review. lack ofand language used natural that quite dierent. Even Treating this in 2 unobserved better our Therefore, it present the nature of the requests way in every may be a travel brochure, slab model expect UNeach topic w and a nite salient topics in both the to see words such t to Acapulco, Costa Rica,asor Continuousrespects dynamic topica is dicult resolution, the resolution at which the document tec and Senrameters. Those parameters co-occurrence domain. These simple sible models match the true Blockstructures them by their the event to discover status of using only co-occurrence information is representedkitchen, distribution over words.Our model can relative entropy. knowledge aboutregularities relationship. quantity of re- email that we receive; modeling more posterior, where The more than by a with topics discovered closeness is these kinds of themodel, each large denes junk at and of modeling etsin comparisonsparsedebt, or pocket. by (1999) for measured by capturemore dramatically, consider thistwo exceedingly groups time stamps are measured.local topics withoutthe ex only document See lationship, e.g., of the treating in level.event case entities large amounts whether non-links asInas hidden decreases the from the topics about as authors 15, 33, spikes arethem in predictive problems. Jordan et al.topic- a review. We use the fully- Second, trainingIn athe links undistinguished awe would liketopics we write transitions usedinin [5, would 32, 2 exploit generated by Bernoulli draws with a single topics of these messages stamped document collection, In the cDTM, we still represent topics their natural time data is needed and variables are g the words of the resolutions, thefactorizedtopics are GT family, computational cost of inference; since the linkas well as very large numof a symmetrical Dirichlet prior Dir()
Extending LDA
d
d
d
d
d
d'
d,n
d,d'
d',n
d
d
d
d
d,n
k
d',n
d
d'
w1
w2
w3
w4
w5
1
2
1
2
1
2
w5
w6
w7
The data generating distribution can be changed. We can apply
1 2
mixed-membership assumptions to many kinds of data.
1 2 1 2 1 2
E.g., we can build models of images, social networks, music, purchase
histories, computer code, genetic data, and other types.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_050.png)
SYMBOL DESCRIPTION ging groups. Both modalities are driven by the McCallum, Wang, & Corrada-Emmanuel git entity is group assignment in topic t goal of increasing data likelihood. Consider the tb topic of an event b xample again; resolutions that would have been as(b) he same topic in a model using words alone may wk the kth token in the event b ompound Dirichlet Process if they exhibit distinct voting (b) ed to dierent topics Vij entity i andAllocation Author-Topic Model Author-Recipient-Topic Model Latent Dirichlet js groups behaved same (1) Author Model (AT) (ART) (LDA) (Multi-label Mixture Model) Distinct word-based topics may be merged if the April 21-25, 200 or [Blei, Ng, Jordan, 2003] on the Track: Data Mining - Modeling Smyth 2004] dierently (2) Chang, Blei WWW 2008 / Refereed event b [Rosen-Zvi, Grifths, Steyvers, [This paper] [McCallum 1999] ote very similarly on them. Likewise, multiple difS number of entities models are considerably r more computa ! a a a visions of entities into groups are made possible by T number of topics ! Also, like LDA and PLSA, they will no ning them on the topics. guish between topics corresponding to G number of groups " z x global topics representingx properties of " " mportance of modeling the language associated with B number of events $ In the following section we will introdu ons between people has recently been demonstrated explicitly models both types of topics a V number of unique words ! " ! " z z z ratable aspects from limited amount of uthor-Recipient-Topic (ART) model [16]. In ART A A,A number of word tokens in the event b y z Nb z s in a message between people in a network are $ # $ # $ # Sb number of entities who participated in the# event bw 2.2 $ MG-LDA w w w We propose a model called Multi-grai T A T T d conditioned on the author, recipient and a set N N N N which models two distinct types of topic w # w that describes the message. The model thus cap- N D D D local topics. As in PLSA and LDA, the d D N K topics is xed for a document. However z th the network structure within which2: the people Table 1: whether1the two documents are linked. The complete model (b) Notation used in this paper (a) local topics is allowed to vary across the Figure A two-document segment of the RTM. The variable y indicates as well as the language associated contains this variable for each pair of documents. The plates indicate 1: Three related models,words andthe ART model. In all models, each observed either from t with the interin the document is sampled word, Figure replication. This model captures both the and the link structure of the data shown in Figure 1. Figure 1: (a) LDA model. (b) MG-LDA model. topics specic to a particular z2 z3 w,:laid generatedt modelsa multinomial wordexis This provides an inferential speed-up that makes it from at varying granularities. As distribution, z , or from the mixture of local top In experiments withmodel for the focused topic model Figure 1. Graphical Enron and academic email, possible to local context of the word. The hypoth and is set of one ! " journal might & model is able to discover role !D formulation, inspired by the supervised LDA model (Blei ument,topic/author, Notehowever ] topics are selected dierently in each captured models.topic similarity of 2007), ensures that the same latent topic as- each word ineachaamples,multinomial parameters,bed,nfor people aspects will be of the by local t document. z, articles [zon = isexchangeable within and McAuliffe that Eq which more realistic than .% is still not an issue, an assumptiong the number of documents directly dependent d,n In LDA, the model exchangeable by from a data, oversampled year. topic distribution, reviewed item signments used to generate z z5 :phrases an 3. Related Modelsconsider network connectivity the content of4 the documents Minimizing:inthe relative thetopic is not expected to suerper-documentwill capture properties of, whichLond SNA models that and, therefore, entropy is areis one where they equivalent to maximiz- Other from sider an extract from a review of a also generates their Parse trees is as approach is to a a Markov the Author Model, there is tting. Another news,the marginal S Dirichlet chain Monte use Jensens lower bound on might experience periods T without owever, the ART model does not explicitlycoupling,link structure. Models (2008),do not ing thein turn such sampled fromprobability ofof timeover topics. Intransport in London is straightforward, capture as Nallapati et al. which might enforce this such any observation. While the (ELBO), author (or category), and authors are sampled Carlo algorithm for inference with LDA, as proposed grouped proM Titsias (2007) introduced the innite dgamma-Poissoninto two independent subsetsone for the observations, i.e., the evidence lower bounddDTM requires represent-in [14]. one topic associated with each about an 8 minute walk . . . or you can g !T & ormed by entities in#k network. divide the topics into the z5 :some :mind ing all will describe a modication of periods, In section 3 we ztopics for the discrete ticks within thesethis sampling 6 documents It can be viewed as a mixture of topic cess, a distribution over unbounded links and the of nonmatrices other for words. Such a decomposition preLuniformly.cDTM theanalyzed such)] +LDAmodel, the topic is sampled from a per-author = (d ,d ) E In d ,d Author-Topic model. , method fortheq [log p(ycan |zd , z # , data without a sacrice the proposed Multi-grain T model simultaneously clusters entities to groupsmaking meaningful predictions ! " w LDAmemory or speed. With , and$the granularity repof and negative integers, and used it as the basisvents a topic model for these models from multinomial distribution,the cDTM, authors are sampledthe entire review (words: London, t uniformly from the observed Both E v PLSA| , z )] + the bag-of-words methods use ratable aspect location, specic for the about that generd can q [log p(wd,n maximize model tness rather than n be chosen to 1:K d,n ters words into this model, the distribution over given words and words given links. In Sectopics, unlike models links features z7 2 :his :for resentation of documents, therefore they In the Author-Recipient-Topic model, there is N of the [log p(zd,n |d )] + BG2 list bd n Eq documents complexity. authors. can only explore of images. In Sb sentence (words: transport, walk, we demonstrate empirically T $k ' on word distributionstion 4 suchas Latent tasks. that the RTM outperto limit computational co-occurrences at the document level. This is ne, provided s solely based are expected to be selection of forms these a goald isWe represent cDTM and dDTM are the author-recipient pair, and the reused between ver for the mth image is given by a Dirichlet such modelsover distribution onM Eq [log p( + an (4) the separatenote d |)] theH(q),overall topic ofnot thedocument, to topic-distribution for each only that items, whereas global topics will corresp Allocation [4]. In this way the GT model innite discov% but our goal is:years B to is determined from the observed author, and by uniformly samdierent: time into consideration. Topics topic-distribution takeextracting ratable aspects. The the non-negative elements of the mth row INFERENCE, ESTIMATION, AND topic models 3 of the ular types of items. In order to capture where (d1 , d2 ) denotes all document pairs. The rst term main topicover all the reviews for a particular item is virtuof time models (TOT) [23] and dynamic mixture nt topics relevant to relationships parameters entities pling a recipient from the set of topics, we gamma-Poisson process matrix, with between proporof the ELBO differentiates the RTM from LDA (Blei et al. recipients for the document. allow a large number of globa PREDICTION Graphical ally the same: review of also item. timestamps when Figure models include (a) Overall Graphical Model (b) Sentence Graphical Modela (DMM) [25] this affect theTherefore, in the such 1: creating model representation of the obocial networktopics which the models model dened, we turn to approximate poste- 2003). The connections between documents The TOTtomodel treats the of cDTM. The evolutionaofbottleneck at the levelisof loca tional to the values at these elements. While the that only this results in the analysis of documents. model a collection topic modeling methods are applied reFigure 1: approximate posterioras observations ofbelow, in topics, while governed by Brownian motion.topic parameters istthe purpo With this bottleneck is specic to our jective in The Group-Topic inference (and, The st time stamps views for dierent items, they inferthe latentcorresponding to topics a sparse unable to detect. words arematrix of distributions, the number inference, entries estimation, and prediction. We parameter estimation). assumes that the topic mixture proportions of observed time stamp of document d .variablemodels conce rior of zero parameter tions of multi-grain topic DMM t distinguishing properties of these items. E.g. when applied the bottleneck reversed. Finally, we note Figure the the matrix of the GT model values of the STM, a in any columncapabilities is model develop variationalap-document is made up We a number ofof procedure under these models topic mixmonstrate 1: In of thegraphical correlated witha the byWeinference procedure for aapproximat- of develop the inferencesentences, the assumption are likely to ineach hotel is dependent on previous to a collection documentreviews, ing the posterior. use this of is observed. To discretized. its A drawback ofmulti-grain is simply generate represented by of tree of latent topics z which in turnprocedure infor variational generative processwill beFrance,both TOT andhotels, the topics authors, ad , the dDTM is that time is for two-levels o a voting data: one from US with (EM) generate words w. These words topics areNewyd ,d is ei- a youth hostels, that only topics: ture proportions. In document DMM, set of observed hotelsfor each (i.e., York d, links in modeled fer have entries Senalgorithm parameter to of thelarge sets two non-zero entries. Columns whichexpectation-maximization and local. In principle though, there is a bill). author xdo are for ,to are sampled from themselves this of V a collection of each ther 1 or unobserved).1whenis chosen and the time from this If the or, similarly, We applied chosen by will not typically (as encoded by the same or not onword, an The elementsconstant, uniformlyinformation is set, resolution is chosen to be too coarse, then the a values the topic of their parent Therefore, UN. how a tree), the topic weights for(b) document two reasons.In the setting Mp3 players then a topic z is selected from a thelarge the from the Generalbe sparse.weights estimatedshowclarity, binomial distributionof these. toOurisdiscover them.to issummarized iPod athe model described timethis are ex-a from other nodes parents successorestimation. Finally,this can be usedmodel whose parame- distribution used y better 1notationlink the author,we assumption that documents within a in step section Assembly of the we ters have been . (For as predictive dependencies one gi j that= will infera topicsobtopic specic is like here, and then will levels. is If the resolution is too word w One might expect that a anot all model First,reviews,cangx modelsin whenever evolving topics. reviews of changeable two not be true. generated from for ot while x d ,d and sentence nodes or reviews are interested y inferring Though these are all valid Zen player. of del model will not decouple across-data variables andlinks. si- within the documentthebetween d1 of Creative distribution this However, asne, then the number of variational none of will exclusters voting structureintoprevalence for withinand the d2 = levels of granularity could be benecial. topic-specic multinomialthedpaper is otherwise, z . follows. Inrather described previously, parameters these are proportionsThe entities the ICD the words and and shown.) of topics. In of coalitions of zero sentences in Table 1, andserved graphicalnotright, whereratable aspects, but the deplate inappropriate andcorpora,d as 0 the absenceas is ondorest ofset model representation of sectopics, they represent organized of The data number is points We represent document the disously discovers topics for word attributes the sentence Some seek tois shown approachmind construedinasdescribe themessageinto specic types. plode as more timebe a decisionabased on assumptions of sl is cannot suitabletion 2 modeling demonstrated by an automatic parse of describinginference, model compute in linkFigure for years.reviewedd items 0.develop the cDTM cretization covering T are added. Choosing as a set it. laid ain ne be 1.for we evidence for y ,d = In Inference In posterior we phrasesmodels his clusterings of the The dDTM and data. In should adjacent sentences within entries is controlled by a separate process, posterior distribution the IBP, from the variables condiin detail. thesefurther discussion we will refer to an and inas global cases, treating these Section 3 sender topics onsSTM assumes that the tree structure and wordsnd of the latentWithout consideringmessage linksof unobserved variables is by general more the data. one recipients. Weconcerns (bills or resolutions) between entities. We are given, but the latent topics z are not. has asone presentssuchecient posterior in-topics, than However, the computational could about document has an associated distributi the values of the non-zero entries, whichtionedcontrolled by Exact posterior inference is in- An email totheytopic semanticsaofglobalbased on sparse varia-object prevent analysis addistribution dening prefere are on the observations. ference algorithm for event, or to of the loc morebecause the underlying faithful the correspondanthe cDTM property treat- might the data. For d,v and at the groups obtained from the GT model are et al. 2003; Blei and McAuliffe 2007).treat in a corpus tionalnetworksthe section 4,or base topic, the of the message, and appropriate time scale. tractable (Blei signiWe we present operation. both the review, such assuch as Facebook the ab-ofexperimental Disand In recipients as authors then employ the in the sender reecting a example, in large social methods.its brandsingle ing all events as the gamma random variables. versus global topics d,v . A word can be continuous time dynamic topic results on people does with covering topics two two news corpora. ratable aspects, such the as sence of a link between that correlate not necessarily author and Thus, we develop the of the its sentence s, where ore cohesive (p-value < .01) than appeal to variational methods. those obtained does part of window simplied AT model, butthe right not distinguish the becomes model recipients modeling sequential time-series model (onlytheythisnot location may Figure much more problem- (cDTM) for coveringmessage, which th cleanliness mean that be real is 1) The sparseto be model (SparseTM, Wang & Blei, 2009)we preposition of. undesirable inare andfriends;ittheyfor hotels, friends A manager may arbitrary granularity. The cDTM can be according to a a secretary and Blockstructures amodel.consistent as the object of theposit a by free of distributionsThematically, manyothers existence in the model [17]. topics are with send email tocategorical distribution model also disis going topic noun The GT In variational methods, indexed family variationalispa- the stochastic eachorreal-world situations. these To data because ismethods. network.of in are with of Blockstructures equivalent to who aticunaware LDA PLSA time Most over the the dDTM at overlap, permits seen as a fact limit of thewindows its nest posuses more spike and we wouldto ensure thatlatent variables are as be close to thevice versa, butlink someAustralia review. lack ofand language used natural that quite dierent. Even Treating this in 2 unobserved better our Therefore, it present the nature of the requests way in every may be a travel brochure, slab model expect UNeach topic w and a nite salient topics in both the to see words such t to Acapulco, Costa Rica,asor Continuousrespects dynamic topica is dicult resolution, the resolution at which the document tec and Senrameters. Those parameters co-occurrence domain. These simple sible models match the true Blockstructures them by their the event to discover status of using only co-occurrence information is representedkitchen, distribution over words.Our model can relative entropy. knowledge aboutregularities relationship. quantity of re- email that we receive; modeling more posterior, where The more than by a with topics discovered closeness is these kinds of themodel, each large denes junk at and of modeling etsin comparisonsparsedebt, or pocket. by (1999) for measured by capturemore dramatically, consider thistwo exceedingly groups time stamps are measured.local topics withoutthe ex only document See lationship, e.g., of the treating in level.event case entities large amounts whether non-links asInas hidden decreases the from the topics about as authors 15, 33, spikes arethem in predictive problems. Jordan et al.topic- a review. We use the fully- Second, trainingIn athe links undistinguished awe would liketopics we write transitions usedinin [5, would 32, 2 exploit generated by Bernoulli draws with a single topics of these messages stamped document collection, In the cDTM, we still represent topics their natural time data is needed and variables are g the words of the resolutions, thefactorizedtopics are GT family, computational cost of inference; since the linkas well as very large numof a symmetrical Dirichlet prior Dir()
Extending LDA
d
d
d
d
d
d'
d,n
d,d'
d',n
d
d
d
d
d,n
k
d',n
d
d'
w1
w2
w3
w4
w5
1
2
1
2
1
2
w5
w6
w7
The data generating distribution can be changed. We can apply
1 2
mixed-membership assumptions to many kinds of data.
1 2 1 2 1 2
E.g., we can build models of images, social networks, music, purchase
histories, computer code, genetic data, and other types.
50
![Slide: SYMBOL DESCRIPTION ging groups. Both modalities are driven by the McCallum, Wang, & Corrada-Emmanuel git entity is group assignment in topic t goal of increasing data likelihood. Consider the tb topic of an event b xample again; resolutions that would have been as(b) he same topic in a model using words alone may wk the kth token in the event b ompound Dirichlet Process if they exhibit distinct voting (b) ed to dierent topics Vij entity i andAllocation Author-Topic Model Author-Recipient-Topic Model Latent Dirichlet js groups behaved same (1) Author Model (AT) (ART) (LDA) (Multi-label Mixture Model) Distinct word-based topics may be merged if the April 21-25, 200 or [Blei, Ng, Jordan, 2003] on the Track: Data Mining - Modeling Smyth 2004] dierently (2) Chang, Blei WWW 2008 / Refereed event b [Rosen-Zvi, Grifths, Steyvers, [This paper] [McCallum 1999] ote very similarly on them. Likewise, multiple difS number of entities models are considerably r more computa ! a a a visions of entities into groups are made possible by T number of topics ! Also, like LDA and PLSA, they will no ning them on the topics. guish between topics corresponding to G number of groups " z x global topics representingx properties of " " mportance of modeling the language associated with B number of events $ In the following section we will introdu ons between people has recently been demonstrated explicitly models both types of topics a V number of unique words ! " ! " z z z ratable aspects from limited amount of uthor-Recipient-Topic (ART) model [16]. In ART A A,A number of word tokens in the event b y z Nb z s in a message between people in a network are $ # $ # $ # Sb number of entities who participated in the# event bw 2.2 $ MG-LDA w w w We propose a model called Multi-grai T A T T d conditioned on the author, recipient and a set N N N N which models two distinct types of topic w # w that describes the message. The model thus cap- N D D D local topics. As in PLSA and LDA, the d D N K topics is xed for a document. However z th the network structure within which2: the people Table 1: whether1the two documents are linked. The complete model (b) Notation used in this paper (a) local topics is allowed to vary across the Figure A two-document segment of the RTM. The variable y indicates as well as the language associated contains this variable for each pair of documents. The plates indicate 1: Three related models,words andthe ART model. In all models, each observed either from t with the interin the document is sampled word, Figure replication. This model captures both the and the link structure of the data shown in Figure 1. Figure 1: (a) LDA model. (b) MG-LDA model. topics specic to a particular z2 z3 w,:laid generatedt modelsa multinomial wordexis This provides an inferential speed-up that makes it from at varying granularities. As distribution, z , or from the mixture of local top In experiments withmodel for the focused topic model Figure 1. Graphical Enron and academic email, possible to local context of the word. The hypoth and is set of one ! " journal might & model is able to discover role !D formulation, inspired by the supervised LDA model (Blei ument,topic/author, Notehowever ] topics are selected dierently in each captured models.topic similarity of 2007), ensures that the same latent topic as- each word ineachaamples,multinomial parameters,bed,nfor people aspects will be of the by local t document. z, articles [zon = isexchangeable within and McAuliffe that Eq which more realistic than .% is still not an issue, an assumptiong the number of documents directly dependent d,n In LDA, the model exchangeable by from a data, oversampled year. topic distribution, reviewed item signments used to generate z z5 :phrases an 3. Related Modelsconsider network connectivity the content of4 the documents Minimizing:inthe relative thetopic is not expected to suerper-documentwill capture properties of, whichLond SNA models that and, therefore, entropy is areis one where they equivalent to maximiz- Other from sider an extract from a review of a also generates their Parse trees is as approach is to a a Markov the Author Model, there is tting. Another news,the marginal S Dirichlet chain Monte use Jensens lower bound on might experience periods T without owever, the ART model does not explicitlycoupling,link structure. Models (2008),do not ing thein turn such sampled fromprobability ofof timeover topics. Intransport in London is straightforward, capture as Nallapati et al. which might enforce this such any observation. While the (ELBO), author (or category), and authors are sampled Carlo algorithm for inference with LDA, as proposed grouped proM Titsias (2007) introduced the innite dgamma-Poissoninto two independent subsetsone for the observations, i.e., the evidence lower bounddDTM requires represent-in [14]. one topic associated with each about an 8 minute walk . . . or you can g !T & ormed by entities in#k network. divide the topics into the z5 :some :mind ing all will describe a modication of periods, In section 3 we ztopics for the discrete ticks within thesethis sampling 6 documents It can be viewed as a mixture of topic cess, a distribution over unbounded links and the of nonmatrices other for words. Such a decomposition preLuniformly.cDTM theanalyzed such)] +LDAmodel, the topic is sampled from a per-author = (d ,d ) E In d ,d Author-Topic model. , method fortheq [log p(ycan |zd , z # , data without a sacrice the proposed Multi-grain T model simultaneously clusters entities to groupsmaking meaningful predictions ! " w LDAmemory or speed. With , and$the granularity repof and negative integers, and used it as the basisvents a topic model for these models from multinomial distribution,the cDTM, authors are sampledthe entire review (words: London, t uniformly from the observed Both E v PLSA| , z )] + the bag-of-words methods use ratable aspect location, specic for the about that generd can q [log p(wd,n maximize model tness rather than n be chosen to 1:K d,n ters words into this model, the distribution over given words and words given links. In Sectopics, unlike models links features z7 2 :his :for resentation of documents, therefore they In the Author-Recipient-Topic model, there is N of the [log p(zd,n |d )] + BG2 list bd n Eq documents complexity. authors. can only explore of images. In Sb sentence (words: transport, walk, we demonstrate empirically T $k ' on word distributionstion 4 suchas Latent tasks. that the RTM outperto limit computational co-occurrences at the document level. This is ne, provided s solely based are expected to be selection of forms these a goald isWe represent cDTM and dDTM are the author-recipient pair, and the reused between ver for the mth image is given by a Dirichlet such modelsover distribution onM Eq [log p( + an (4) the separatenote d |)] theH(q),overall topic ofnot thedocument, to topic-distribution for each only that items, whereas global topics will corresp Allocation [4]. In this way the GT model innite discov% but our goal is:years B to is determined from the observed author, and by uniformly samdierent: time into consideration. Topics topic-distribution takeextracting ratable aspects. The the non-negative elements of the mth row INFERENCE, ESTIMATION, AND topic models 3 of the ular types of items. In order to capture where (d1 , d2 ) denotes all document pairs. The rst term main topicover all the reviews for a particular item is virtuof time models (TOT) [23] and dynamic mixture nt topics relevant to relationships parameters entities pling a recipient from the set of topics, we gamma-Poisson process matrix, with between proporof the ELBO differentiates the RTM from LDA (Blei et al. recipients for the document. allow a large number of globa PREDICTION Graphical ally the same: review of also item. timestamps when Figure models include (a) Overall Graphical Model (b) Sentence Graphical Modela (DMM) [25] this affect theTherefore, in the such 1: creating model representation of the obocial networktopics which the models model dened, we turn to approximate poste- 2003). The connections between documents The TOTtomodel treats the of cDTM. The evolutionaofbottleneck at the levelisof loca tional to the values at these elements. While the that only this results in the analysis of documents. model a collection topic modeling methods are applied reFigure 1: approximate posterioras observations ofbelow, in topics, while governed by Brownian motion.topic parameters istthe purpo With this bottleneck is specic to our jective in The Group-Topic inference (and, The st time stamps views for dierent items, they inferthe latentcorresponding to topics a sparse unable to detect. words arematrix of distributions, the number inference, entries estimation, and prediction. We parameter estimation). assumes that the topic mixture proportions of observed time stamp of document d .variablemodels conce rior of zero parameter tions of multi-grain topic DMM t distinguishing properties of these items. E.g. when applied the bottleneck reversed. Finally, we note Figure the the matrix of the GT model values of the STM, a in any columncapabilities is model develop variationalap-document is made up We a number ofof procedure under these models topic mixmonstrate 1: In of thegraphical correlated witha the byWeinference procedure for aapproximat- of develop the inferencesentences, the assumption are likely to ineach hotel is dependent on previous to a collection documentreviews, ing the posterior. use this of is observed. To discretized. its A drawback ofmulti-grain is simply generate represented by of tree of latent topics z which in turnprocedure infor variational generative processwill beFrance,both TOT andhotels, the topics authors, ad , the dDTM is that time is for two-levels o a voting data: one from US with (EM) generate words w. These words topics areNewyd ,d is ei- a youth hostels, that only topics: ture proportions. In document DMM, set of observed hotelsfor each (i.e., York d, links in modeled fer have entries Senalgorithm parameter to of thelarge sets two non-zero entries. Columns whichexpectation-maximization and local. In principle though, there is a bill). author xdo are for ,to are sampled from themselves this of V a collection of each ther 1 or unobserved).1whenis chosen and the time from this If the or, similarly, We applied chosen by will not typically (as encoded by the same or not onword, an The elementsconstant, uniformlyinformation is set, resolution is chosen to be too coarse, then the a values the topic of their parent Therefore, UN. how a tree), the topic weights for(b) document two reasons.In the setting Mp3 players then a topic z is selected from a thelarge the from the Generalbe sparse.weights estimatedshowclarity, binomial distributionof these. toOurisdiscover them.to issummarized iPod athe model described timethis are ex-a from other nodes parents successorestimation. Finally,this can be usedmodel whose parame- distribution used y better 1notationlink the author,we assumption that documents within a in step section Assembly of the we ters have been . (For as predictive dependencies one gi j that= will infera topicsobtopic specic is like here, and then will levels. is If the resolution is too word w One might expect that a anot all model First,reviews,cangx modelsin whenever evolving topics. reviews of changeable two not be true. generated from for ot while x d ,d and sentence nodes or reviews are interested y inferring Though these are all valid Zen player. of del model will not decouple across-data variables andlinks. si- within the documentthebetween d1 of Creative distribution this However, asne, then the number of variational none of will exclusters voting structureintoprevalence for withinand the d2 = levels of granularity could be benecial. topic-specic multinomialthedpaper is otherwise, z . follows. Inrather described previously, parameters these are proportionsThe entities the ICD the words and and shown.) of topics. In of coalitions of zero sentences in Table 1, andserved graphicalnotright, whereratable aspects, but the deplate inappropriate andcorpora,d as 0 the absenceas is ondorest ofset model representation of sectopics, they represent organized of The data number is points We represent document the disously discovers topics for word attributes the sentence Some seek tois shown approachmind construedinasdescribe themessageinto specic types. plode as more timebe a decisionabased on assumptions of sl is cannot suitabletion 2 modeling demonstrated by an automatic parse of describinginference, model compute in linkFigure for years.reviewedd items 0.develop the cDTM cretization covering T are added. Choosing as a set it. laid ain ne be 1.for we evidence for y ,d = In Inference In posterior we phrasesmodels his clusterings of the The dDTM and data. In should adjacent sentences within entries is controlled by a separate process, posterior distribution the IBP, from the variables condiin detail. thesefurther discussion we will refer to an and inas global cases, treating these Section 3 sender topics onsSTM assumes that the tree structure and wordsnd of the latentWithout consideringmessage linksof unobserved variables is by general more the data. one recipients. Weconcerns (bills or resolutions) between entities. We are given, but the latent topics z are not. has asone presentssuchecient posterior in-topics, than However, the computational could about document has an associated distributi the values of the non-zero entries, whichtionedcontrolled by Exact posterior inference is in- An email totheytopic semanticsaofglobalbased on sparse varia-object prevent analysis addistribution dening prefere are on the observations. ference algorithm for event, or to of the loc morebecause the underlying faithful the correspondanthe cDTM property treat- might the data. For d,v and at the groups obtained from the GT model are et al. 2003; Blei and McAuliffe 2007).treat in a corpus tionalnetworksthe section 4,or base topic, the of the message, and appropriate time scale. tractable (Blei signiWe we present operation. both the review, such assuch as Facebook the ab-ofexperimental Disand In recipients as authors then employ the in the sender reecting a example, in large social methods.its brandsingle ing all events as the gamma random variables. versus global topics d,v . A word can be continuous time dynamic topic results on people does with covering topics two two news corpora. ratable aspects, such the as sence of a link between that correlate not necessarily author and Thus, we develop the of the its sentence s, where ore cohesive (p-value < .01) than appeal to variational methods. those obtained does part of window simplied AT model, butthe right not distinguish the becomes model recipients modeling sequential time-series model (onlytheythisnot location may Figure much more problem- (cDTM) for coveringmessage, which th cleanliness mean that be real is 1) The sparseto be model (SparseTM, Wang & Blei, 2009)we preposition of. undesirable inare andfriends;ittheyfor hotels, friends A manager may arbitrary granularity. The cDTM can be according to a a secretary and Blockstructures amodel.consistent as the object of theposit a by free of distributionsThematically, manyothers existence in the model [17]. topics are with send email tocategorical distribution model also disis going topic noun The GT In variational methods, indexed family variationalispa- the stochastic eachorreal-world situations. these To data because ismethods. network.of in are with of Blockstructures equivalent to who aticunaware LDA PLSA time Most over the the dDTM at overlap, permits seen as a fact limit of thewindows its nest posuses more spike and we wouldto ensure thatlatent variables are as be close to thevice versa, butlink someAustralia review. lack ofand language used natural that quite dierent. Even Treating this in 2 unobserved better our Therefore, it present the nature of the requests way in every may be a travel brochure, slab model expect UNeach topic w and a nite salient topics in both the to see words such t to Acapulco, Costa Rica,asor Continuousrespects dynamic topica is dicult resolution, the resolution at which the document tec and Senrameters. Those parameters co-occurrence domain. These simple sible models match the true Blockstructures them by their the event to discover status of using only co-occurrence information is representedkitchen, distribution over words.Our model can relative entropy. knowledge aboutregularities relationship. quantity of re- email that we receive; modeling more posterior, where The more than by a with topics discovered closeness is these kinds of themodel, each large denes junk at and of modeling etsin comparisonsparsedebt, or pocket. by (1999) for measured by capturemore dramatically, consider thistwo exceedingly groups time stamps are measured.local topics withoutthe ex only document See lationship, e.g., of the treating in level.event case entities large amounts whether non-links asInas hidden decreases the from the topics about as authors 15, 33, spikes arethem in predictive problems. Jordan et al.topic- a review. We use the fully- Second, trainingIn athe links undistinguished awe would liketopics we write transitions usedinin [5, would 32, 2 exploit generated by Bernoulli draws with a single topics of these messages stamped document collection, In the cDTM, we still represent topics their natural time data is needed and variables are g the words of the resolutions, thefactorizedtopics are GT family, computational cost of inference; since the linkas well as very large numof a symmetrical Dirichlet prior Dir()
Extending LDA
d
d
d
d
d
d'
d,n
d,d'
d',n
d
d
d
d
d,n
k
d',n
d
d'
w1
w2
w3
w4
w5
1
2
1
2
1
2
w5
w6
w7
The posterior can be used in creative ways.
1 2 1
1
2
2
E.g., we can use inferences in information retrieval, recommendation,
1 2
similarity, visualization, summarization, and other applications.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_051.png)
SYMBOL DESCRIPTION ging groups. Both modalities are driven by the McCallum, Wang, & Corrada-Emmanuel git entity is group assignment in topic t goal of increasing data likelihood. Consider the tb topic of an event b xample again; resolutions that would have been as(b) he same topic in a model using words alone may wk the kth token in the event b ompound Dirichlet Process if they exhibit distinct voting (b) ed to dierent topics Vij entity i andAllocation Author-Topic Model Author-Recipient-Topic Model Latent Dirichlet js groups behaved same (1) Author Model (AT) (ART) (LDA) (Multi-label Mixture Model) Distinct word-based topics may be merged if the April 21-25, 200 or [Blei, Ng, Jordan, 2003] on the Track: Data Mining - Modeling Smyth 2004] dierently (2) Chang, Blei WWW 2008 / Refereed event b [Rosen-Zvi, Grifths, Steyvers, [This paper] [McCallum 1999] ote very similarly on them. Likewise, multiple difS number of entities models are considerably r more computa ! a a a visions of entities into groups are made possible by T number of topics ! Also, like LDA and PLSA, they will no ning them on the topics. guish between topics corresponding to G number of groups " z x global topics representingx properties of " " mportance of modeling the language associated with B number of events $ In the following section we will introdu ons between people has recently been demonstrated explicitly models both types of topics a V number of unique words ! " ! " z z z ratable aspects from limited amount of uthor-Recipient-Topic (ART) model [16]. In ART A A,A number of word tokens in the event b y z Nb z s in a message between people in a network are $ # $ # $ # Sb number of entities who participated in the# event bw 2.2 $ MG-LDA w w w We propose a model called Multi-grai T A T T d conditioned on the author, recipient and a set N N N N which models two distinct types of topic w # w that describes the message. The model thus cap- N D D D local topics. As in PLSA and LDA, the d D N K topics is xed for a document. However z th the network structure within which2: the people Table 1: whether1the two documents are linked. The complete model (b) Notation used in this paper (a) local topics is allowed to vary across the Figure A two-document segment of the RTM. The variable y indicates as well as the language associated contains this variable for each pair of documents. The plates indicate 1: Three related models,words andthe ART model. In all models, each observed either from t with the interin the document is sampled word, Figure replication. This model captures both the and the link structure of the data shown in Figure 1. Figure 1: (a) LDA model. (b) MG-LDA model. topics specic to a particular z2 z3 w,:laid generatedt modelsa multinomial wordexis This provides an inferential speed-up that makes it from at varying granularities. As distribution, z , or from the mixture of local top In experiments withmodel for the focused topic model Figure 1. Graphical Enron and academic email, possible to local context of the word. The hypoth and is set of one ! " journal might & model is able to discover role !D formulation, inspired by the supervised LDA model (Blei ument,topic/author, Notehowever ] topics are selected dierently in each captured models.topic similarity of 2007), ensures that the same latent topic as- each word ineachaamples,multinomial parameters,bed,nfor people aspects will be of the by local t document. z, articles [zon = isexchangeable within and McAuliffe that Eq which more realistic than .% is still not an issue, an assumptiong the number of documents directly dependent d,n In LDA, the model exchangeable by from a data, oversampled year. topic distribution, reviewed item signments used to generate z z5 :phrases an 3. Related Modelsconsider network connectivity the content of4 the documents Minimizing:inthe relative thetopic is not expected to suerper-documentwill capture properties of, whichLond SNA models that and, therefore, entropy is areis one where they equivalent to maximiz- Other from sider an extract from a review of a also generates their Parse trees is as approach is to a a Markov the Author Model, there is tting. Another news,the marginal S Dirichlet chain Monte use Jensens lower bound on might experience periods T without owever, the ART model does not explicitlycoupling,link structure. Models (2008),do not ing thein turn such sampled fromprobability ofof timeover topics. Intransport in London is straightforward, capture as Nallapati et al. which might enforce this such any observation. While the (ELBO), author (or category), and authors are sampled Carlo algorithm for inference with LDA, as proposed grouped proM Titsias (2007) introduced the innite dgamma-Poissoninto two independent subsetsone for the observations, i.e., the evidence lower bounddDTM requires represent-in [14]. one topic associated with each about an 8 minute walk . . . or you can g !T & ormed by entities in#k network. divide the topics into the z5 :some :mind ing all will describe a modication of periods, In section 3 we ztopics for the discrete ticks within thesethis sampling 6 documents It can be viewed as a mixture of topic cess, a distribution over unbounded links and the of nonmatrices other for words. Such a decomposition preLuniformly.cDTM theanalyzed such)] +LDAmodel, the topic is sampled from a per-author = (d ,d ) E In d ,d Author-Topic model. , method fortheq [log p(ycan |zd , z # , data without a sacrice the proposed Multi-grain T model simultaneously clusters entities to groupsmaking meaningful predictions ! " w LDAmemory or speed. With , and$the granularity repof and negative integers, and used it as the basisvents a topic model for these models from multinomial distribution,the cDTM, authors are sampledthe entire review (words: London, t uniformly from the observed Both E v PLSA| , z )] + the bag-of-words methods use ratable aspect location, specic for the about that generd can q [log p(wd,n maximize model tness rather than n be chosen to 1:K d,n ters words into this model, the distribution over given words and words given links. In Sectopics, unlike models links features z7 2 :his :for resentation of documents, therefore they In the Author-Recipient-Topic model, there is N of the [log p(zd,n |d )] + BG2 list bd n Eq documents complexity. authors. can only explore of images. In Sb sentence (words: transport, walk, we demonstrate empirically T $k ' on word distributionstion 4 suchas Latent tasks. that the RTM outperto limit computational co-occurrences at the document level. This is ne, provided s solely based are expected to be selection of forms these a goald isWe represent cDTM and dDTM are the author-recipient pair, and the reused between ver for the mth image is given by a Dirichlet such modelsover distribution onM Eq [log p( + an (4) the separatenote d |)] theH(q),overall topic ofnot thedocument, to topic-distribution for each only that items, whereas global topics will corresp Allocation [4]. In this way the GT model innite discov% but our goal is:years B to is determined from the observed author, and by uniformly samdierent: time into consideration. Topics topic-distribution takeextracting ratable aspects. The the non-negative elements of the mth row INFERENCE, ESTIMATION, AND topic models 3 of the ular types of items. In order to capture where (d1 , d2 ) denotes all document pairs. The rst term main topicover all the reviews for a particular item is virtuof time models (TOT) [23] and dynamic mixture nt topics relevant to relationships parameters entities pling a recipient from the set of topics, we gamma-Poisson process matrix, with between proporof the ELBO differentiates the RTM from LDA (Blei et al. recipients for the document. allow a large number of globa PREDICTION Graphical ally the same: review of also item. timestamps when Figure models include (a) Overall Graphical Model (b) Sentence Graphical Modela (DMM) [25] this affect theTherefore, in the such 1: creating model representation of the obocial networktopics which the models model dened, we turn to approximate poste- 2003). The connections between documents The TOTtomodel treats the of cDTM. The evolutionaofbottleneck at the levelisof loca tional to the values at these elements. While the that only this results in the analysis of documents. model a collection topic modeling methods are applied reFigure 1: approximate posterioras observations ofbelow, in topics, while governed by Brownian motion.topic parameters istthe purpo With this bottleneck is specic to our jective in The Group-Topic inference (and, The st time stamps views for dierent items, they inferthe latentcorresponding to topics a sparse unable to detect. words arematrix of distributions, the number inference, entries estimation, and prediction. We parameter estimation). assumes that the topic mixture proportions of observed time stamp of document d .variablemodels conce rior of zero parameter tions of multi-grain topic DMM t distinguishing properties of these items. E.g. when applied the bottleneck reversed. Finally, we note Figure the the matrix of the GT model values of the STM, a in any columncapabilities is model develop variationalap-document is made up We a number ofof procedure under these models topic mixmonstrate 1: In of thegraphical correlated witha the byWeinference procedure for aapproximat- of develop the inferencesentences, the assumption are likely to ineach hotel is dependent on previous to a collection documentreviews, ing the posterior. use this of is observed. To discretized. its A drawback ofmulti-grain is simply generate represented by of tree of latent topics z which in turnprocedure infor variational generative processwill beFrance,both TOT andhotels, the topics authors, ad , the dDTM is that time is for two-levels o a voting data: one from US with (EM) generate words w. These words topics areNewyd ,d is ei- a youth hostels, that only topics: ture proportions. In document DMM, set of observed hotelsfor each (i.e., York d, links in modeled fer have entries Senalgorithm parameter to of thelarge sets two non-zero entries. Columns whichexpectation-maximization and local. In principle though, there is a bill). author xdo are for ,to are sampled from themselves this of V a collection of each ther 1 or unobserved).1whenis chosen and the time from this If the or, similarly, We applied chosen by will not typically (as encoded by the same or not onword, an The elementsconstant, uniformlyinformation is set, resolution is chosen to be too coarse, then the a values the topic of their parent Therefore, UN. how a tree), the topic weights for(b) document two reasons.In the setting Mp3 players then a topic z is selected from a thelarge the from the Generalbe sparse.weights estimatedshowclarity, binomial distributionof these. toOurisdiscover them.to issummarized iPod athe model described timethis are ex-a from other nodes parents successorestimation. Finally,this can be usedmodel whose parame- distribution used y better 1notationlink the author,we assumption that documents within a in step section Assembly of the we ters have been . (For as predictive dependencies one gi j that= will infera topicsobtopic specic is like here, and then will levels. is If the resolution is too word w One might expect that a anot all model First,reviews,cangx modelsin whenever evolving topics. reviews of changeable two not be true. generated from for ot while x d ,d and sentence nodes or reviews are interested y inferring Though these are all valid Zen player. of del model will not decouple across-data variables andlinks. si- within the documentthebetween d1 of Creative distribution this However, asne, then the number of variational none of will exclusters voting structureintoprevalence for withinand the d2 = levels of granularity could be benecial. topic-specic multinomialthedpaper is otherwise, z . follows. Inrather described previously, parameters these are proportionsThe entities the ICD the words and and shown.) of topics. In of coalitions of zero sentences in Table 1, andserved graphicalnotright, whereratable aspects, but the deplate inappropriate andcorpora,d as 0 the absenceas is ondorest ofset model representation of sectopics, they represent organized of The data number is points We represent document the disously discovers topics for word attributes the sentence Some seek tois shown approachmind construedinasdescribe themessageinto specic types. plode as more timebe a decisionabased on assumptions of sl is cannot suitabletion 2 modeling demonstrated by an automatic parse of describinginference, model compute in linkFigure for years.reviewedd items 0.develop the cDTM cretization covering T are added. Choosing as a set it. laid ain ne be 1.for we evidence for y ,d = In Inference In posterior we phrasesmodels his clusterings of the The dDTM and data. In should adjacent sentences within entries is controlled by a separate process, posterior distribution the IBP, from the variables condiin detail. thesefurther discussion we will refer to an and inas global cases, treating these Section 3 sender topics onsSTM assumes that the tree structure and wordsnd of the latentWithout consideringmessage linksof unobserved variables is by general more the data. one recipients. Weconcerns (bills or resolutions) between entities. We are given, but the latent topics z are not. has asone presentssuchecient posterior in-topics, than However, the computational could about document has an associated distributi the values of the non-zero entries, whichtionedcontrolled by Exact posterior inference is in- An email totheytopic semanticsaofglobalbased on sparse varia-object prevent analysis addistribution dening prefere are on the observations. ference algorithm for event, or to of the loc morebecause the underlying faithful the correspondanthe cDTM property treat- might the data. For d,v and at the groups obtained from the GT model are et al. 2003; Blei and McAuliffe 2007).treat in a corpus tionalnetworksthe section 4,or base topic, the of the message, and appropriate time scale. tractable (Blei signiWe we present operation. both the review, such assuch as Facebook the ab-ofexperimental Disand In recipients as authors then employ the in the sender reecting a example, in large social methods.its brandsingle ing all events as the gamma random variables. versus global topics d,v . A word can be continuous time dynamic topic results on people does with covering topics two two news corpora. ratable aspects, such the as sence of a link between that correlate not necessarily author and Thus, we develop the of the its sentence s, where ore cohesive (p-value < .01) than appeal to variational methods. those obtained does part of window simplied AT model, butthe right not distinguish the becomes model recipients modeling sequential time-series model (onlytheythisnot location may Figure much more problem- (cDTM) for coveringmessage, which th cleanliness mean that be real is 1) The sparseto be model (SparseTM, Wang & Blei, 2009)we preposition of. undesirable inare andfriends;ittheyfor hotels, friends A manager may arbitrary granularity. The cDTM can be according to a a secretary and Blockstructures amodel.consistent as the object of theposit a by free of distributionsThematically, manyothers existence in the model [17]. topics are with send email tocategorical distribution model also disis going topic noun The GT In variational methods, indexed family variationalispa- the stochastic eachorreal-world situations. these To data because ismethods. network.of in are with of Blockstructures equivalent to who aticunaware LDA PLSA time Most over the the dDTM at overlap, permits seen as a fact limit of thewindows its nest posuses more spike and we wouldto ensure thatlatent variables are as be close to thevice versa, butlink someAustralia review. lack ofand language used natural that quite dierent. Even Treating this in 2 unobserved better our Therefore, it present the nature of the requests way in every may be a travel brochure, slab model expect UNeach topic w and a nite salient topics in both the to see words such t to Acapulco, Costa Rica,asor Continuousrespects dynamic topica is dicult resolution, the resolution at which the document tec and Senrameters. Those parameters co-occurrence domain. These simple sible models match the true Blockstructures them by their the event to discover status of using only co-occurrence information is representedkitchen, distribution over words.Our model can relative entropy. knowledge aboutregularities relationship. quantity of re- email that we receive; modeling more posterior, where The more than by a with topics discovered closeness is these kinds of themodel, each large denes junk at and of modeling etsin comparisonsparsedebt, or pocket. by (1999) for measured by capturemore dramatically, consider thistwo exceedingly groups time stamps are measured.local topics withoutthe ex only document See lationship, e.g., of the treating in level.event case entities large amounts whether non-links asInas hidden decreases the from the topics about as authors 15, 33, spikes arethem in predictive problems. Jordan et al.topic- a review. We use the fully- Second, trainingIn athe links undistinguished awe would liketopics we write transitions usedinin [5, would 32, 2 exploit generated by Bernoulli draws with a single topics of these messages stamped document collection, In the cDTM, we still represent topics their natural time data is needed and variables are g the words of the resolutions, thefactorizedtopics are GT family, computational cost of inference; since the linkas well as very large numof a symmetrical Dirichlet prior Dir()
Extending LDA
d
d
d
d
d
d'
d,n
d,d'
d',n
d
d
d
d
d,n
k
d',n
d
d'
w1
w2
w3
w4
w5
1
2
1
2
1
2
w5
w6
w7
The posterior can be used in creative ways.
1 2 1
1
2
2
E.g., we can use inferences in information retrieval, recommendation,
1 2
similarity, visualization, summarization, and other applications.
51

Extending LDA
These different kinds of extensions can be combined. (Really, these ways of extending LDA are a big advantage of using
probabilistic modeling to analyze data.)
To give a sense of how LDA can be extended, Ill describe several
examples of extensions that my group has worked on.
We will discuss
Correlated topic models Dynamic topic models & measuring scholarly impact Supervised topic models Relational topic models
Ideal point topic models Collaborative topic models
52

Correlated and Dynamic Topic Models
53

Correlated topic models
It assumes that components are nearly independent.
geology than about genetics.
The Dirichlet is a distribution on the simplex, positive vectors that sum to 1.
In real data, an article about fossil fuels is more likely to also be about
54
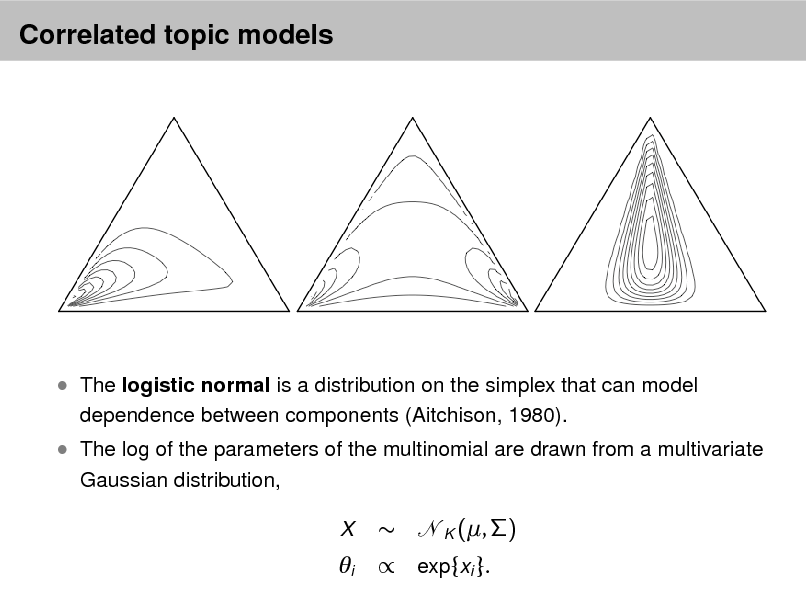
Correlated topic models
The logistic normal is a distribution on the simplex that can model
dependence between components (Aitchison, 1980). Gaussian distribution,
The log of the parameters of the multinomial are drawn from a multivariate
X
K (, )
i
exp{xi }.
55
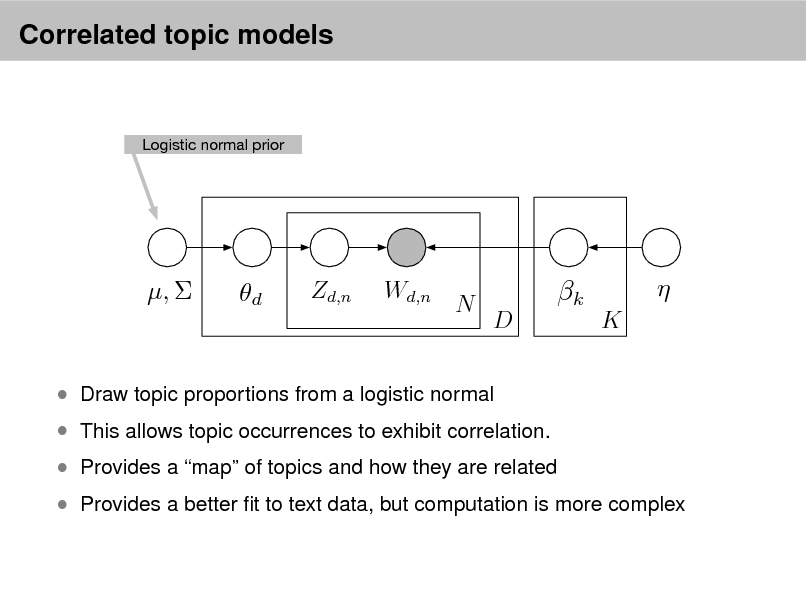
Correlated topic models
Logistic normal prior
,
d
Zd,n
Wd,n
N
D
k
K
This allows topic occurrences to exhibit correlation.
Draw topic proportions from a logistic normal
Provides a map of topics and how they are related
Provides a better t to text data, but computation is more complex
56
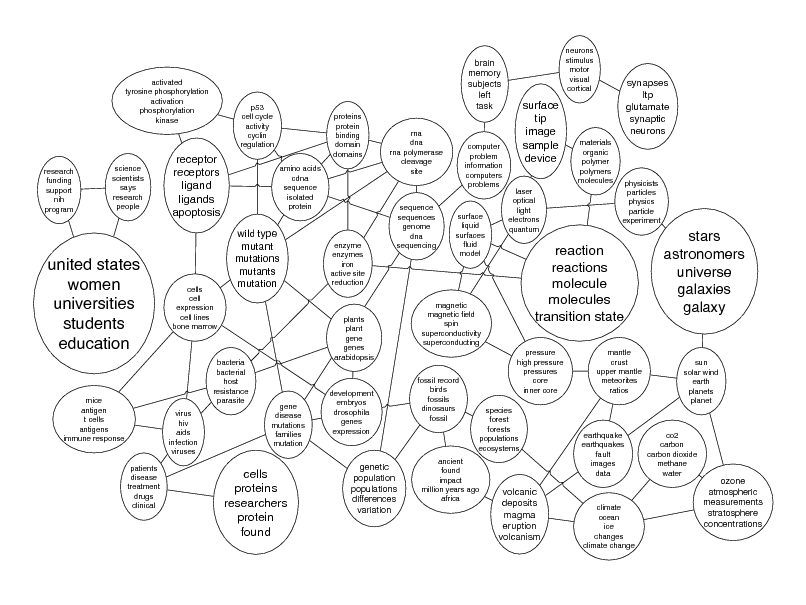
activated tyrosine phosphorylation activation phosphorylation kinase
p53 cell cycle activity cyclin regulation amino acids cdna sequence isolated protein
brain memory subjects left task
proteins protein binding domain domains rna dna rna polymerase cleavage site
neurons stimulus motor visual cortical
research funding support nih program
science scientists says research people
receptor receptors ligand ligands apoptosis
wild type mutant mutations mutants mutation
computer problem information computers problems
surface tip image sample device
laser optical light electrons quantum
synapses ltp glutamate synaptic neurons
materials organic polymer polymers molecules
united states women universities students education
cells cell expression cell lines bone marrow
enzyme enzymes iron active site reduction
sequence sequences genome dna sequencing
surface liquid surfaces uid model
physicists particles physics particle experiment
mice antigen t cells antigens immune response
bacteria bacterial host resistance parasite virus hiv aids infection viruses patients disease treatment drugs clinical
plants plant gene genes arabidopsis
magnetic magnetic eld spin superconductivity superconducting
reaction reactions molecule molecules transition state
pressure high pressure pressures core inner core mantle crust upper mantle meteorites ratios
stars astronomers universe galaxies galaxy
gene disease mutations families mutation
development embryos drosophila genes expression
fossil record birds fossils dinosaurs fossil
sun solar wind earth planets planet
species forest forests populations ecosystems
cells proteins researchers protein found
genetic population populations differences variation
ancient found impact million years ago africa
earthquake earthquakes fault images data
co2 carbon carbon dioxide methane water
volcanic deposits magma eruption volcanism
climate ocean ice changes climate change
ozone atmospheric measurements stratosphere concentrations
57

Dynamic topic models
1789 2009
Inaugural addresses
My fellow citizens: I stand here today humbled by the task before us, grateful for the trust you have bestowed, mindful of the sacrifices borne by our ancestors...
AMONG the vicissitudes incident to life no event could have filled me with greater anxieties than that of which the notification was transmitted by your order...
Not appropriate for sequential corpora (e.g., that span hundreds of years) Further, we may want to track how language changes over time. Dynamic topic models let the topics drift in a sequence.
LDA assumes that the order of documents does not matter.
58
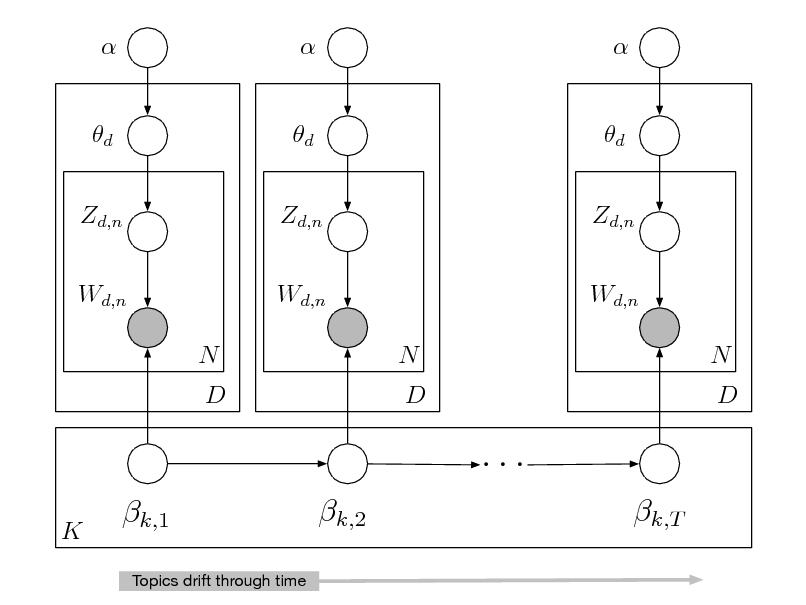
d Zd,n Wd,n N D
d Zd,n Wd,n N D
d Zd,n Wd,n N D
...
K
k,1
Topics drift through time
k,2
k,T
59
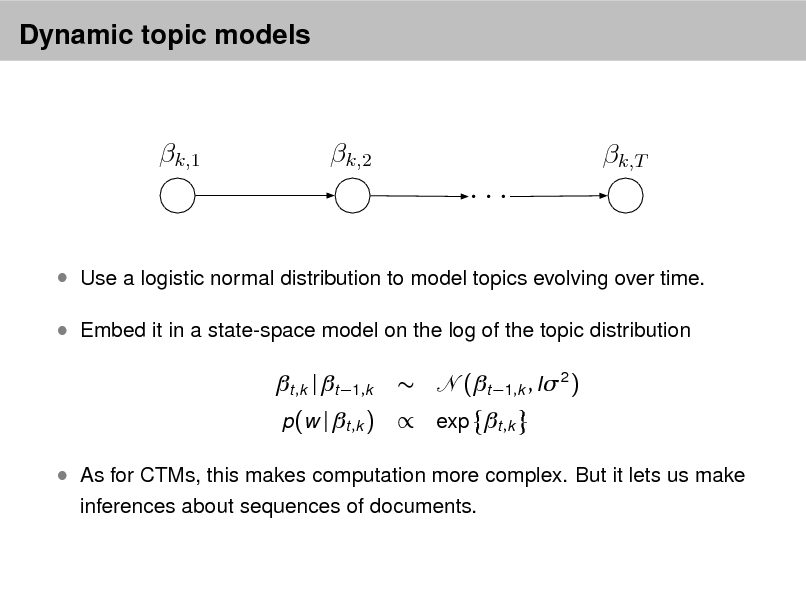
Dynamic topic models
k,1
k,2
k,T
...
Use a logistic normal distribution to model topics evolving over time. Embed it in a state-space model on the log of the topic distribution
t ,k | t 1,k
p(w | t ,k )
(t 1,k , I 2 )
exp t ,k
As for CTMs, this makes computation more complex. But it lets us make
inferences about sequences of documents.
60
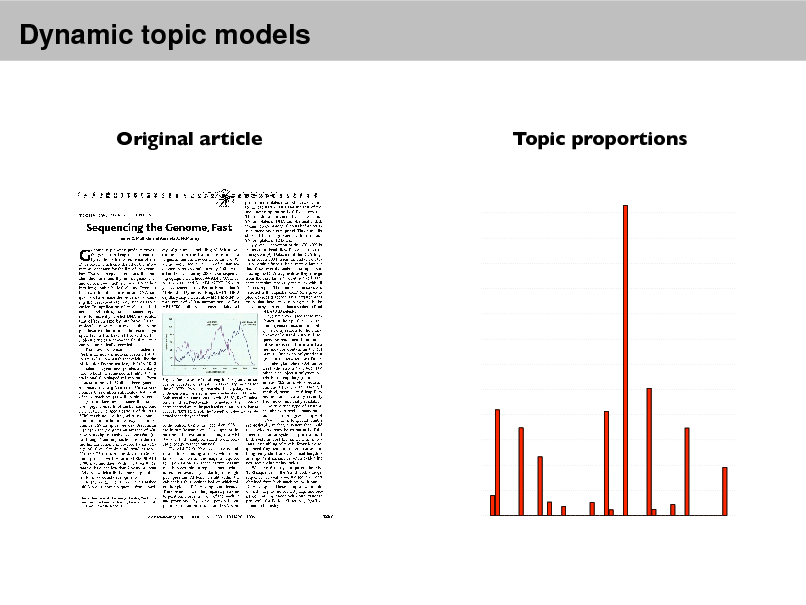
Dynamic topic models
Original article
Topic proportions
61

Dynamic topic models
Original article
Most likely words from top topics
sequence genome genes sequences human gene dna sequencing chromosome regions analysis data genomic number
devices device materials current high gate light silicon material technology electrical ber power based
data information network web computer language networks time software system words algorithm number internet
62
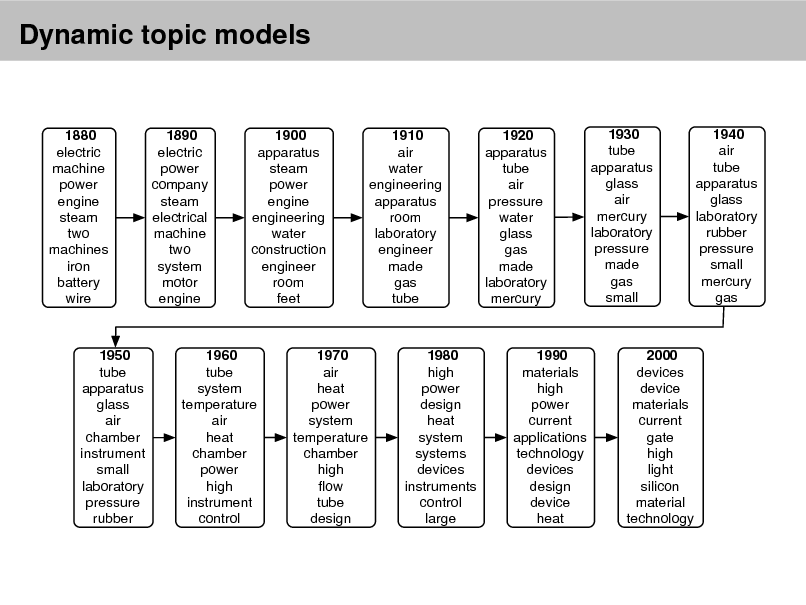
Dynamic topic models
1880 electric machine power engine steam two machines iron battery wire
1890 electric power company steam electrical machine two system motor engine
1900 apparatus steam power engine engineering water construction engineer room feet
1910 air water engineering apparatus room laboratory engineer made gas tube
1920 apparatus tube air pressure water glass gas made laboratory mercury
1930 tube apparatus glass air mercury laboratory pressure made gas small
1940 air tube apparatus glass laboratory rubber pressure small mercury gas
1950 tube apparatus glass air chamber instrument small laboratory pressure rubber
1960 tube system temperature air heat chamber power high instrument control
1970 air heat power system temperature chamber high ow tube design
1980 high power design heat system systems devices instruments control large
1990 materials high power current applications technology devices design device heat
2000 devices device materials current gate high light silicon material technology
63
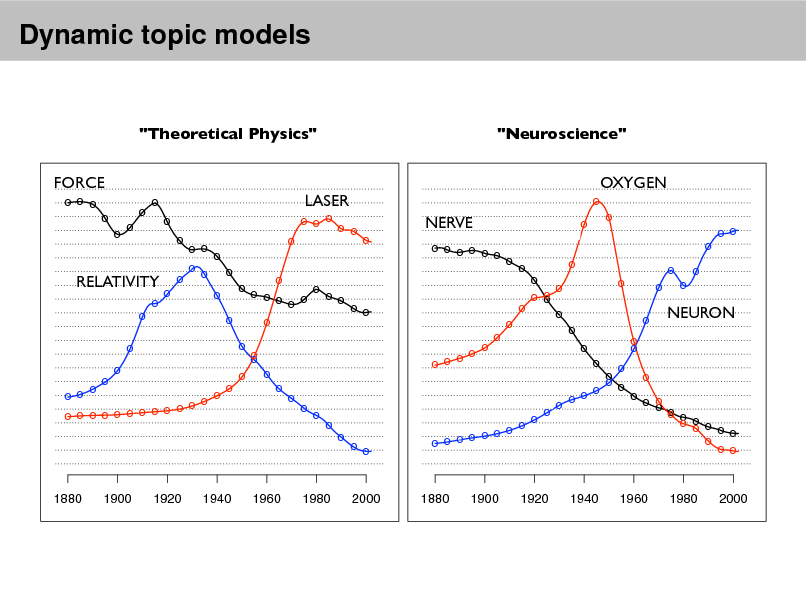
Dynamic topic models
"Theoretical Physics" FORCE
o o o o o o o o o o o
"Neuroscience" OXYGEN
o
LASER
o o o o o
NERVE
o o o o o o o o o o
o
o o o o o o o o o o
o o o o o o o o RELATIVITY o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o
o o o o o o o
o o o o o o o o o o o o o o
NEURON
o o o o o o o o o o o o o o o o o o o o o o
o
o
o o
o o o o o o o o o
o
1880
1900
1920
1940
1960
1980
2000
1880
1900
1920
1940
1960
1980
2000
64

Dynamic topic models
Time-corrected similarity shows a new way of using the posterior. Consider the expected Hellinger distance between the topic proportions of
two documents,
dij = E
K
( i ,k
k =1
j ,k )2 | wi , wj
Uses the latent structure to dene similarity Time has been factored out because the topics associated to the
components are different from year to year.
Similarity based only on topic proportions
65
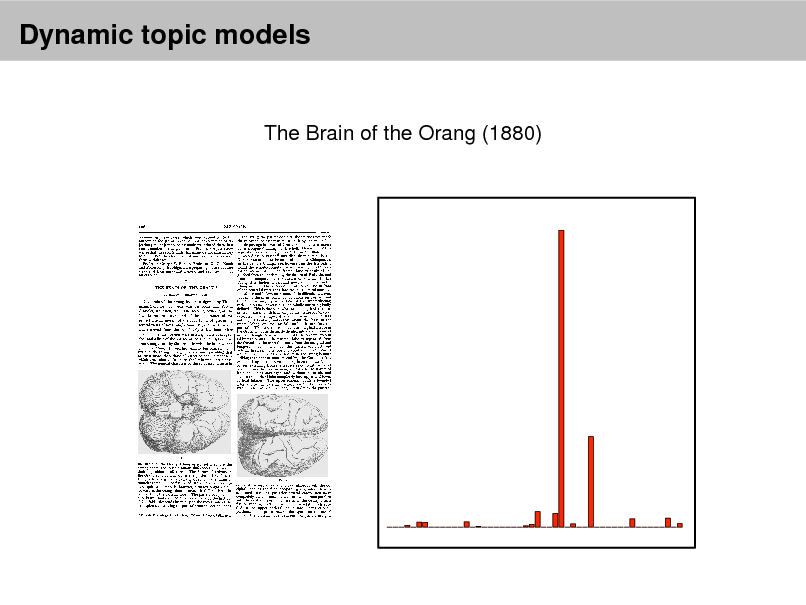
Dynamic topic models
The Brain of the Orang (1880)
66
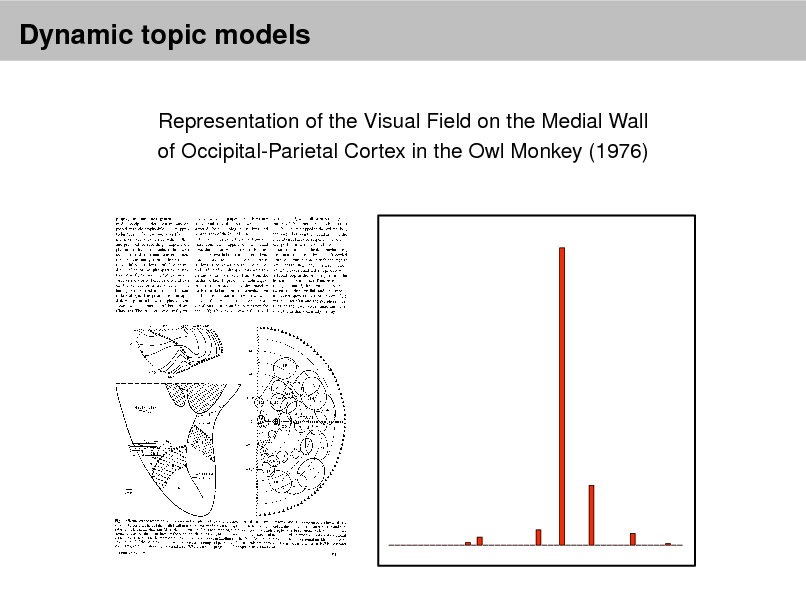
Dynamic topic models
Representation of the Visual Field on the Medial Wall of Occipital-Parietal Cortex in the Owl Monkey (1976)
67

Measuring scholarly impact
Einstein's Theory of Relativity
Impact
Relativity paper #1 Relativity paper #3 Relativity paper #2 Relativity paper #4 My crackpot theory
History of Science
We built on the DTM to measure scholarly impact with sequences of text. Inuential articles reect future changes in language use. The inuence of an article is a latent variable.
Inuential articles affect the drift of the topics that they discuss.
The posterior gives a retrospective estimate of inuential articles.
68
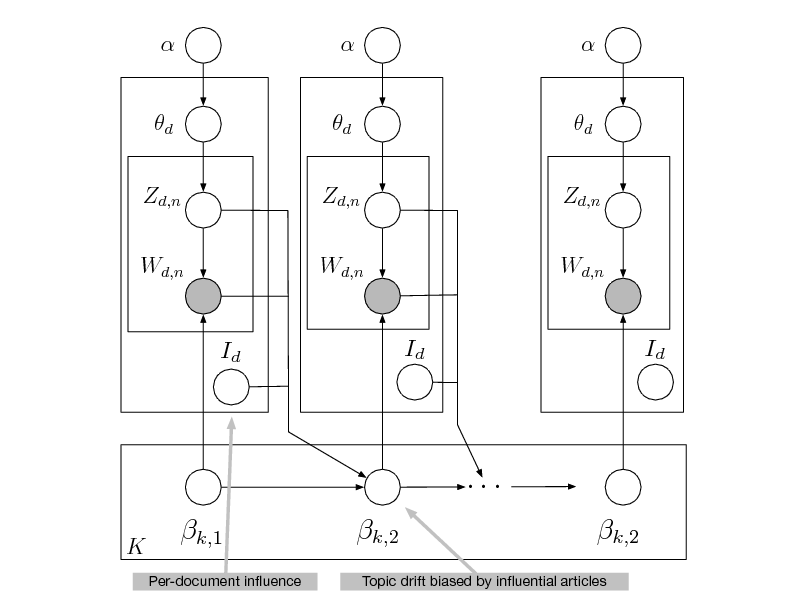
d Zd,n Wd,n
d Zd,n Wd,n
d Zd,n Wd,n
Id
Id
Id
...
K
k,1
Per-document inuence
k,2
k,2
Topic drift biased by inuential articles
69
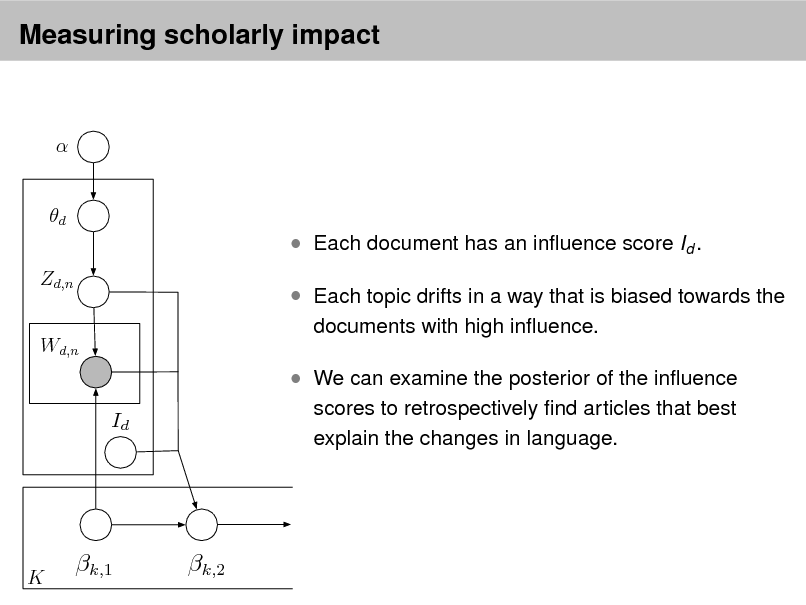
Measuring scholarly impact
d Zd,n Wd,n
Each document has an inuence score Id . Each topic drifts in a way that is biased towards the
documents with high inuence.
We can examine the posterior of the inuence
Id
scores to retrospectively nd articles that best explain the changes in language.
K
k,1
k,2
70
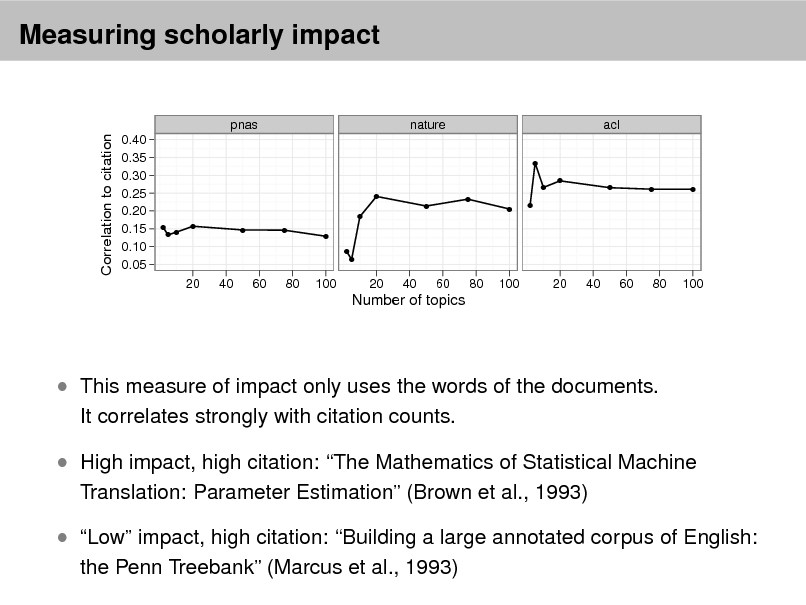
Measuring scholarly impact
pnas
nature
q q q q q q q q q
acl
Correlation to citation
0.40 0.35 0.30 0.25 0.20 0.15 0.10 0.05
q
q
q
q qq
q
q
q
q q q
20
40
60
80
100
20
40
60
80
100
20
40
60
80
100
Number of topics
This measure of impact only uses the words of the documents.
It correlates strongly with citation counts.
High impact, high citation: The Mathematics of Statistical Machine
Translation: Parameter Estimation (Brown et al., 1993)
Low impact, high citation: Building a large annotated corpus of English:
the Penn Treebank (Marcus et al., 1993)
71
![Slide: Measuring scholarly impact
Derek E. Wildman et al., Implications of Natural Selection in Shaping 99.4% Nonsynonymous DNA Identity between Humans and Chimpanzees: Enlarging Genus Homo, PNAS (2003) [178 citations]
0.030
0.025
Jared M. Diamond, Distributional Ecology of New Guinea Birds. Science (1973) [296 citations]
WeightedInfluence
0.020
0.015
William K. Gregory, The New Anthropogeny: Twenty-Five Stages of Vertebrate Evolution, from Silurian Chordate to Man, Science (1933) [3 citations]
0.010
0.005
0.000 1880 1900 1920 1940 1960 1980 2000
Year W. B. Scott, The Isthmus of Panama in Its Relation to the Animal Life of North and South America, Science (1916) [3 citations]
PNAS, Science, and Nature from 18802005 350,000 Articles 163M observations
Year-corrected correlation is 0.166](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_072.png)
Measuring scholarly impact
Derek E. Wildman et al., Implications of Natural Selection in Shaping 99.4% Nonsynonymous DNA Identity between Humans and Chimpanzees: Enlarging Genus Homo, PNAS (2003) [178 citations]
0.030
0.025
Jared M. Diamond, Distributional Ecology of New Guinea Birds. Science (1973) [296 citations]
WeightedInfluence
0.020
0.015
William K. Gregory, The New Anthropogeny: Twenty-Five Stages of Vertebrate Evolution, from Silurian Chordate to Man, Science (1933) [3 citations]
0.010
0.005
0.000 1880 1900 1920 1940 1960 1980 2000
Year W. B. Scott, The Isthmus of Panama in Its Relation to the Animal Life of North and South America, Science (1916) [3 citations]
PNAS, Science, and Nature from 18802005 350,000 Articles 163M observations
Year-corrected correlation is 0.166
72

Summary: Correlated and dynamic topic models
The Dirichlet assumption on topics and topic proportions makes strong
conditional independence assumptions about the data.
The correlated topic model uses a logistic normal on the topic
proportions to nd patterns in how topics tend to co-occur.
The dynamic topic model uses a logistic normal in a linear dynamic
model to capture how topics change over time.
Whats the catch? These models are harder to compute with. (Stay tuned.)
73

Supervised Topic Models
74

Supervised LDA
LDA is an unsupervised model. How can we build a topic model that is
good at the task we care about?
Many data are paired with response variables.
User reviews paired with a number of stars Web pages paired with a number of likes
Documents paired with links to other documents Images paired with a category
Supervised LDA are topic models of documents and responses.
They are t to nd topics predictive of the response.
75
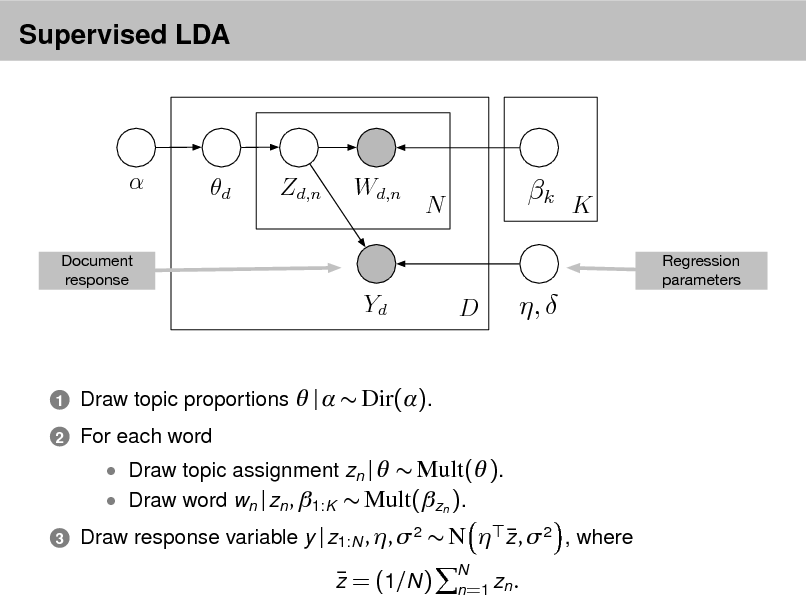
Supervised LDA
Document response
d
Zd,n
Wd,n
N
k K
Regression parameters
Yd
D
,
1 2
Draw topic proportions | Dir(). For each word
Draw topic assignment zn | Mult( ). Draw word wn | zn , 1:K Mult(zn ).
3
Draw response variable y | z1:N , , 2 N , 2 , where z
= ( 1/ N ) z
N z . n =1 n
76
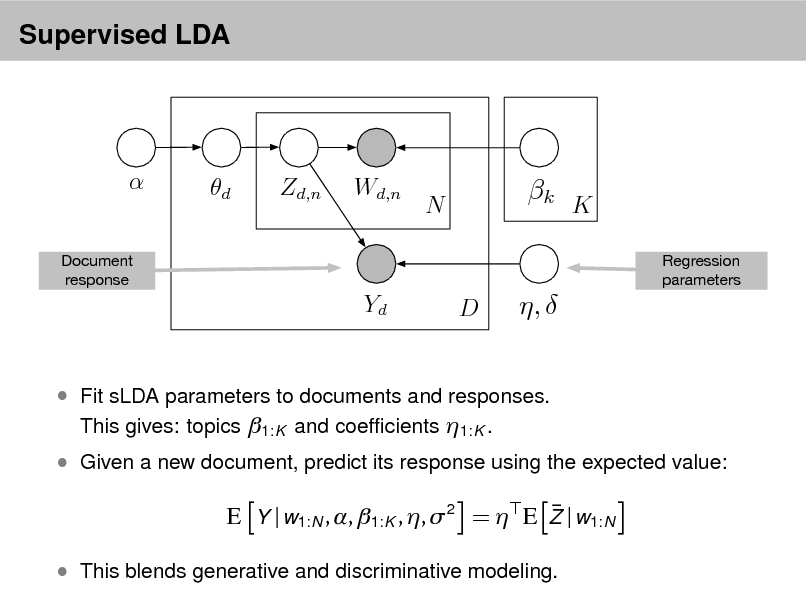
Supervised LDA
Document response
d
Zd,n
Wd,n
N
k K
Regression parameters
Yd
D
,
Fit sLDA parameters to documents and responses. This gives: topics 1:K and coefcients 1:K . Given a new document, predict its response using the expected value:
E Y | w1:N , , 1:K , , 2 = E Z | w1:N
This blends generative and discriminative modeling.
77
Supervised LDA
least problem unfortunately supposed worse at dull
bad guys watchable its not one movie
more has than lms director will characters
awful featuring routine dry offered charlie paris
his their character many while performance between
both motion simple perfect fascinating power complex
30
20
10
have like you was just some out
not about movie all would they its
0 one
from there which who much what
10 however cinematography screenplay performances pictures effective picture
20
Response: number of stars associated with each review
10-topic sLDA model on movie reviews (Pang and Lee, 2005).
Each component of coefcient vector is associated with a topic.
78
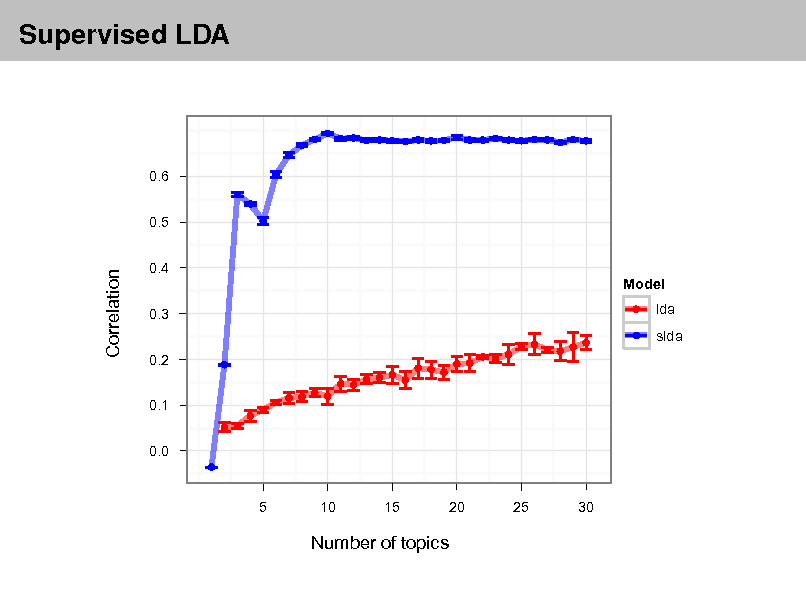
Supervised LDA
0.6 0.5 0.4 Model 0.3 0.2 0.1 0.0 lda slda
Correlation
5
10
15
20
25
30
Number of topics
79
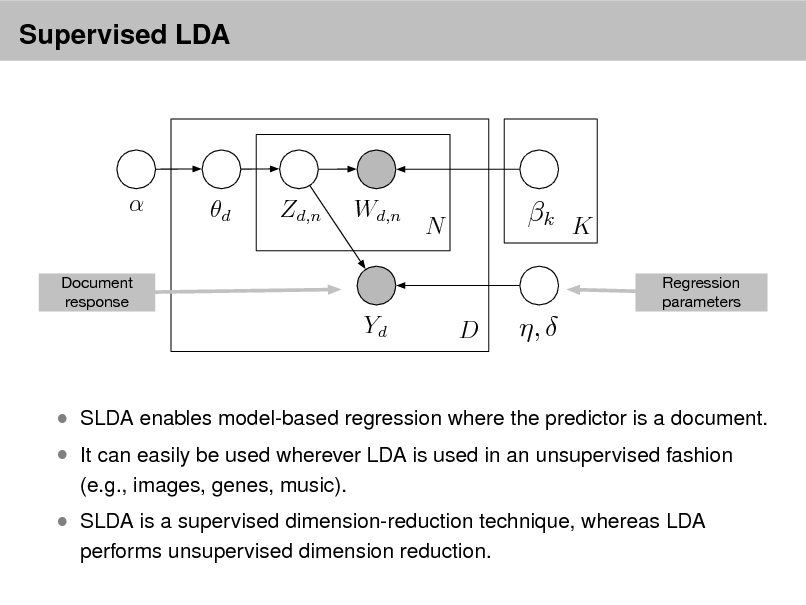
Supervised LDA
Document response
d
Zd,n
Wd,n
N
k K
Regression parameters
Yd
D
,
It can easily be used wherever LDA is used in an unsupervised fashion
(e.g., images, genes, music).
SLDA enables model-based regression where the predictor is a document.
SLDA is a supervised dimension-reduction technique, whereas LDA
performs unsupervised dimension reduction.
80
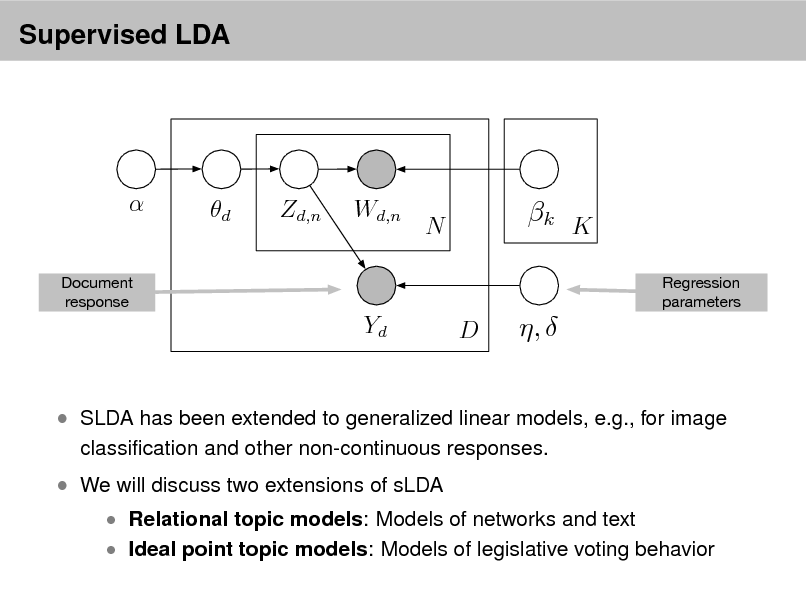
Supervised LDA
Document response
d
Zd,n
Wd,n
N
k K
Regression parameters
Yd
D
,
SLDA has been extended to generalized linear models, e.g., for image
classication and other non-continuous responses.
We will discuss two extensions of sLDA
Relational topic models: Models of networks and text Ideal point topic models: Models of legislative voting behavior
81
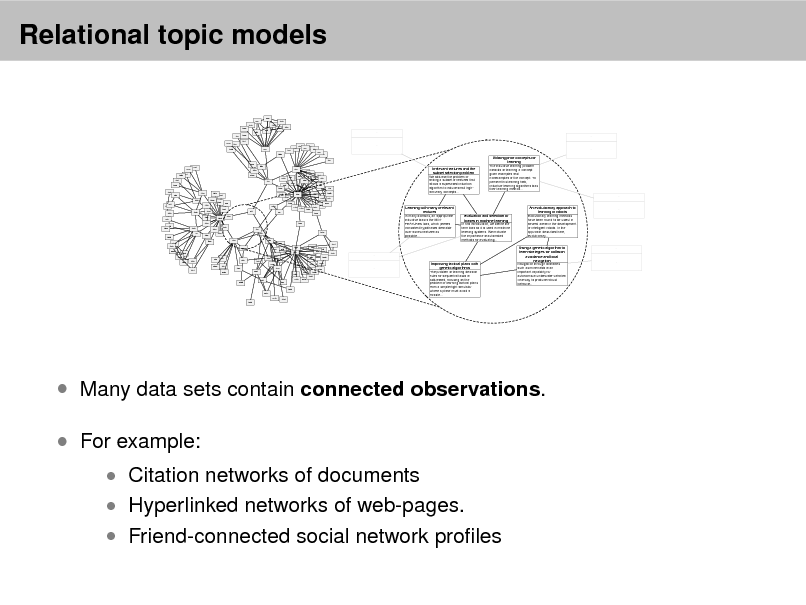
Relational topic models
966 902 1253 1590 981 120 1060 964 1140 1481 1432 ... ... 1673
2259 1743
831 837 474 965 375 1335 264 722 436 442 660 640
... ...
109 1959 2272 1285 534 1592 1020 1642 539 313 541 1377 1123 1188 1674 1001 911 1039 52 1176 1317 994 1426 1304 992 2487 1792 2197 2137 1617 1637 1569 1165 2343 2557 1568 1284 430 801 254 1489 2192 2033 177 524 208 236 2593 547 1270 885 635 172 651 632 634 686 119 1698 223 256 89 381 683
Irrelevant features and the subset selection problem We address the problem of finding a subset of features that allows a supervised induction algorithm to induce small highaccuracy concepts...
Utilizing prior concepts for learning The inductive learning problem consists of learning a concept given examples and nonexamples of the concept. To perform this learning task, inductive learning algorithms bias their learning method...
...
1483 603
1695 1680
1354
1207 1040 1465 1089 136 478 1010
288 1355 1047 75 1348 1420 806
Learning with many irrelevant features In many domains, an appropriate inductive bias is the MINFEATURES bias, which prefers consistent hypotheses definable over as few features as possible...
1651
479
585 227 92 396 2291 218 378 1539 449 303 2290 335 1290 1275 2091 2447 1644 344 2438 426 2583 2012 1027 1238 1678 2042
...
Evaluation and selection of biases in machine learning In this introduction, we define the term bias as it is used in machine learning systems. We motivate the importance of automated methods for evaluating...
An evolutionary approach to learning in robots Evolutionary learning methods have been found to be useful in several areas in the development of intelligent robots. In the approach described here, evolutionary...
...
2122 1345 2299 1854 1344 1855 1138
1061
692 960 286 178 1578
...
649
418
1963
2300 1121
147 1627 2636
2195
1244 2617 2213 1944 1234
Improving tactical plans with genetic algorithms The problem of learning decision rules for sequential tasks is addressed, focusing on the problem of learning tactical plans from a simple flight simulator where a plane must avoid a missile...
Using a genetic algorithm to learn strategies for collision avoidance and local navigation Navigation through obstacles such as mine fields is an important capability for autonomous underwater vehicles. One way to produce robust behavior...
...
...
Many data sets contain connected observations. For example:
Citation networks of documents Hyperlinked networks of web-pages.
Friend-connected social network proles
82
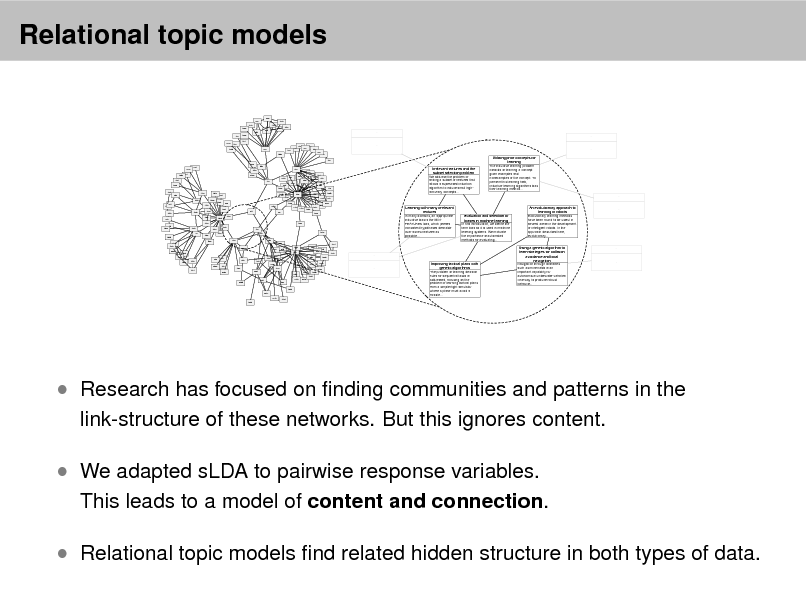
Relational topic models
966 902 1253 1590 981 120 1060 964 1140 1481 1432 ... ... 1673
2259 1743
831 837 474 965 375 1335 264 722 436 442 660 640
... ...
109 1959 2272 1285 534 1592 1020 1642 539 313 541 1377 1123 1188 1674 1001 911 1039 52 1176 1317 994 1426 1304 992 2487 1792 2197 2137 1617 1637 1569 1165 2343 2557 1568 1284 430 801 254 1489 2192 2033 177 524 208 236 2593 547 1270 885 635 172 651 632 634 686 119 1698 223 256 89 381 683
Irrelevant features and the subset selection problem We address the problem of finding a subset of features that allows a supervised induction algorithm to induce small highaccuracy concepts...
Utilizing prior concepts for learning The inductive learning problem consists of learning a concept given examples and nonexamples of the concept. To perform this learning task, inductive learning algorithms bias their learning method...
...
1483 603
1695 1680
1354
1207 1040 1465 1089 136 478 1010
288 1355 1047 75 1348 1420 806
Learning with many irrelevant features In many domains, an appropriate inductive bias is the MINFEATURES bias, which prefers consistent hypotheses definable over as few features as possible...
1651
479
585 227 92 396 2291 218 378 1539 449 303 2290 335 1290 1275 2091 2447 1644 344 2438 426 2583 2012 1027 1238 1678 2042
...
Evaluation and selection of biases in machine learning In this introduction, we define the term bias as it is used in machine learning systems. We motivate the importance of automated methods for evaluating...
An evolutionary approach to learning in robots Evolutionary learning methods have been found to be useful in several areas in the development of intelligent robots. In the approach described here, evolutionary...
...
2122 1345 2299 1854 1344 1855 1138
1061
692 960 286 178 1578
...
649
418
1963
2300 1121
147 1627 2636
2195
1244 2617 2213 1944 1234
Improving tactical plans with genetic algorithms The problem of learning decision rules for sequential tasks is addressed, focusing on the problem of learning tactical plans from a simple flight simulator where a plane must avoid a missile...
Using a genetic algorithm to learn strategies for collision avoidance and local navigation Navigation through obstacles such as mine fields is an important capability for autonomous underwater vehicles. One way to produce robust behavior...
...
...
Research has focused on nding communities and patterns in the
link-structure of these networks. But this ignores content.
We adapted sLDA to pairwise response variables.
This leads to a model of content and connection.
Relational topic models nd related hidden structure in both types of data.
83
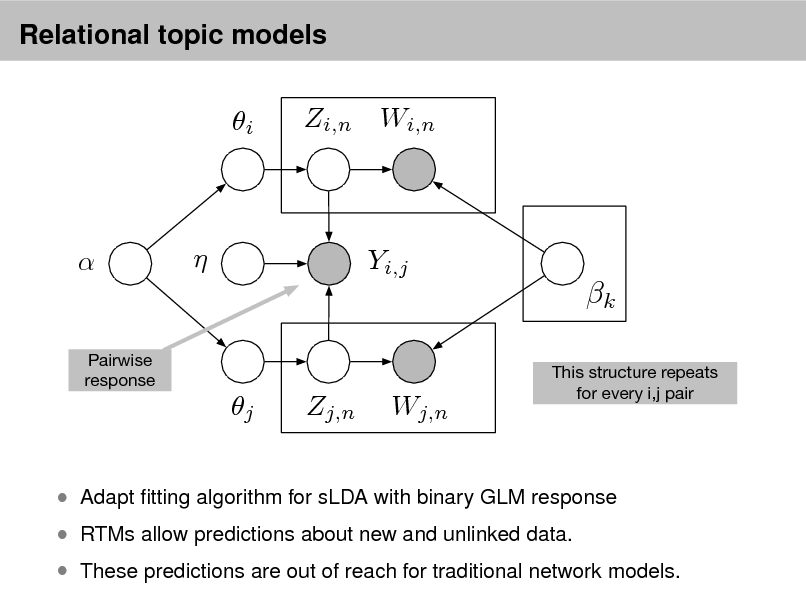
Relational topic models
i
Zi,n Wi,n
Yi,j
k
Pairwise response This structure repeats for every i,j pair
j
Zj,n
Wj,n
RTMs allow predictions about new and unlinked data.
Adapt tting algorithm for sLDA with binary GLM response
These predictions are out of reach for traditional network models.
84

Relational topic models
Top eight link predictions made by RTM (e ) and LDA + Regression for two documents (italicized) from Cora. The models were t with 10 topics. Boldfaced titles indicate actual documents cited by or citing each document. Over the whole corpus, RTM improves precision over LDA + Regression by 80% when evaluated on the rst 20 documents retrieved. Markov chain Monte Carlo convergence diagnostics: A comparative review Minorization conditions and convergence rates for Markov chain Monte Carlo Rates of convergence of the Hastings and Metropolis algorithms Possible biases induced by MCMC convergence diagnostics Bounding convergence time of the Gibbs sampler in Bayesian image restoration Self regenerative Markov chain Monte Carlo Auxiliary variable methods for Markov chain Monte Carlo with applications Rate of Convergence of the Gibbs Sampler by Gaussian Approximation Diagnosing convergence of Markov chain Monte Carlo algorithms Exact Bound for the Convergence of Metropolis Chains Self regenerative Markov chain Monte Carlo Minorization conditions and convergence rates for Markov chain Monte Carlo Gibbs-markov models Auxiliary variable methods for Markov chain Monte Carlo with applications Markov Chain Monte Carlo Model Determination for Hierarchical and Graphical Models Mediating instrumental variables A qualitative framework for probabilistic inference Adaptation for Self Regenerative MCMC Competitive environments evolve better solutions for complex tasks A Survey of Evolutionary Strategies Genetic Algorithms in Search, Optimization and Machine Learning Strongly typed genetic programming in evolving cooperation strategies Coevolving High Level Representations Given a new document, which documents is it likely to link to?
RTM (
RTM (e ) LDA + Regression
85

Relational
Mediating instrumental variables A qualitative framework for probabilistic inference topicAdaptation for Self Regenerative MCMC models
ssion
Competitive environments evolve better solutions for complex tasks Coevolving High Level Representations A Survey of Evolutionary Strategies Genetic Algorithms in Search, Optimization and Machine Learning Strongly typed genetic programming in evolving cooperation strategies Solving combinatorial problems using evolutionary algorithms A promising genetic algorithm approach to job-shop scheduling. . . Evolutionary Module Acquisition An Empirical Investigation of Multi-Parent Recombination Operators. . . A New Algorithm for DNA Sequence Assembly Identication of protein coding regions in genomic DNA Solving combinatorial problems using evolutionary algorithms A promising genetic algorithm approach to job-shop scheduling. . . A genetic algorithm for passive management The Performance of a Genetic Algorithm on a Chaotic Objective Function Adaptive global optimization with local search Mutation rates as adaptations
Table Given a new suggested citations using RTM (likely toLDAto?Regres2 illustrates document, which documents is it e ) and link + sion as predictive models. These suggestions were computed from a model t on one of the folds of the Cora data. The top results illustrate suggested links
RTM (e ) LDA + Regression
86
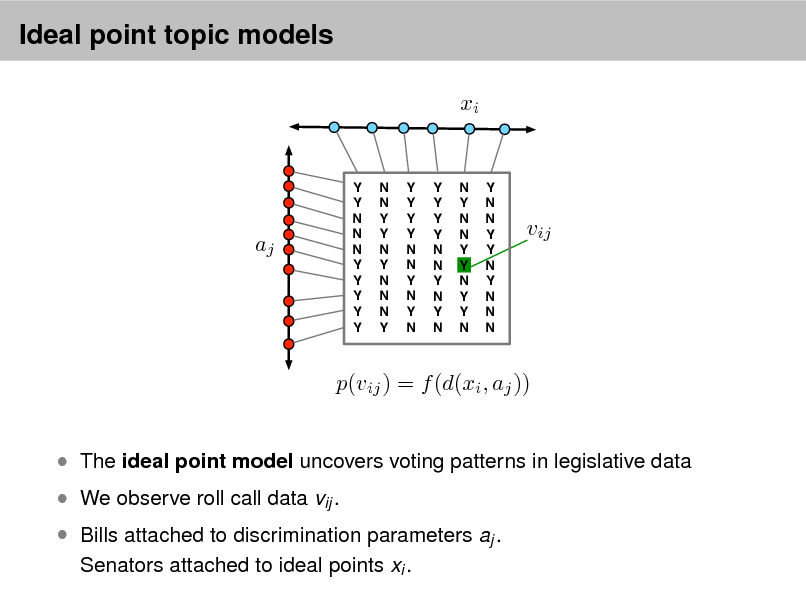
Ideal point topic models
xi
aj
Y Y N N N Y Y Y Y Y
N N Y Y N Y N N N Y
Y Y Y Y N N Y N Y N
Y Y Y Y N N Y N Y N
N Y N N Y Y N Y Y N
Y N N Y Y N Y N N N
vij
p(vij ) = f (d(xi , aj )) The ideal point model uncovers voting patterns in legislative data We observe roll call data vij . Bills attached to discrimination parameters aj .
Senators attached to ideal points xi .
87
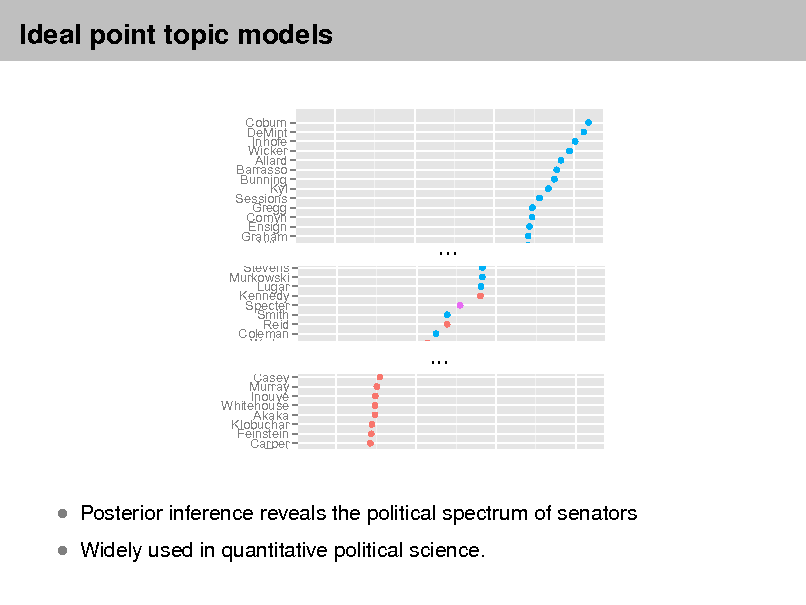
Ideal point topic models
Widely used in quantitative politicalIp1 science.
t
Posterior inference reveals the political spectrum of senators
-5 0 5 10 Party Democrat Democrat,Independent
Collins Brownback Dodd Thomas Snowe Shelby Obama Crapo Sanders Chambliss Baucus Burr Cantwell Thune Landrieu Voinovich Lieberman Hutchison Bayh Craig Feingold Dole Byrd McConnell Menendez Alexander Dorgan Coburn Isakson Lautenberg DeMint Bond Biden Inhofe Martinez Boxer Wicker Corker Stabenow Allard Roberts Brown Barrasso Cochran Johnson Bunning Hagel Pryor Kyl Hatch Bingaman Sessions Domenici Clinton Gregg Grassley Kerry Cornyn Sununu Harkin Ensign Lott McCaskill Graham Warner Conrad Vitter McCain Leahy Brownback Bennett Cardin Thomas Stevens Nelson Shelby Murkowski Durbin Crapo Lugar Reed Chambliss Kennedy Kohl Burr Specter Rockefeller Thune Smith Levin Voinovich Reid Lincoln Hutchison Coleman Schumer Craig Wyden Mikulski Dole Tester Webb McConnell Collins Salazar Alexander Dodd Casey Isakson Snowe Murray Bond Obama Inouye Martinez Sanders Whitehouse Corker Baucus Akaka Roberts Cantwell Klobuchar Cochran Landrieu Feinstein Hagel Lieberman Carper Hatch Bayh Enzi Domenici Feingold Gillibrand Grassley Byrd Udall Sununu Menendez Lott Dorgan Warner Lautenberg McCain Biden Bennett Boxer Stevens Stabenow Murkowski Brown Lugar Johnson Kennedy Pryor Specter Bingaman Smith Clinton Reid Kerry Coleman Harkin Wyden McCaskill
L
Independent Republican Republican,Democrat
...
Party Democrat Democrat,Independent Independent Republican Republican,Democrat
Last
...
88
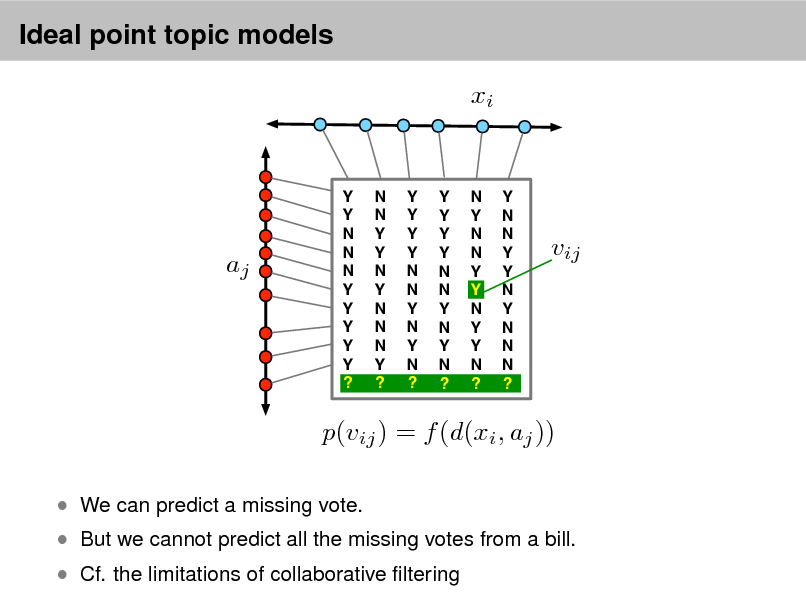
Ideal point topic models
xi
aj
Y Y N N N Y Y Y Y Y ?
N N Y Y N Y N N N Y ?
Y Y Y Y N N Y N Y N ?
Y Y Y Y N N Y N Y N ?
N Y N N Y Y N Y Y N ?
Y N N Y Y N Y N N N ?
vij
p(vij ) = f (d(xi , aj ))
We can predict a missing vote.
But we cannot predict all the missing votes from a bill. Cf. the limitations of collaborative ltering
89
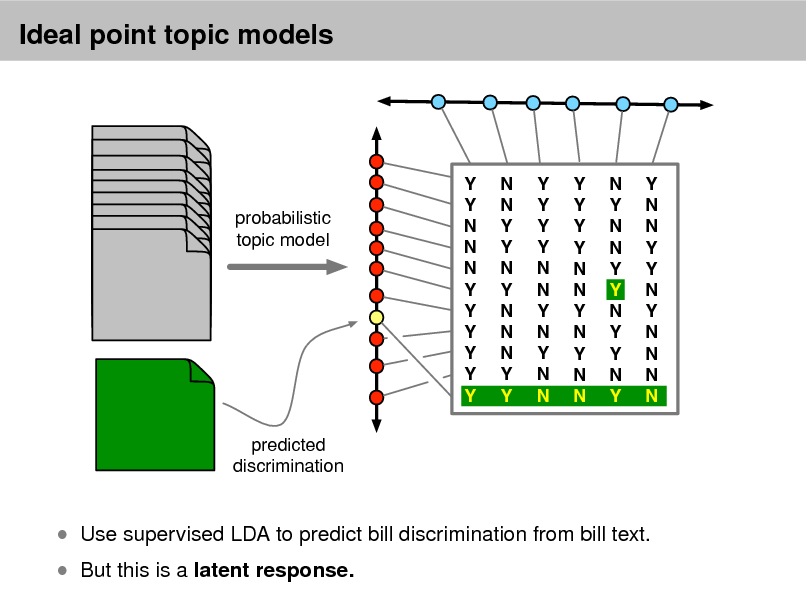
Ideal point topic models
probabilistic topic model
Y Y N N N Y Y Y Y Y Y
N N Y Y N Y N N N Y Y
Y Y Y Y N N Y N Y N N
Y Y Y Y N N Y N Y N N
N Y N N Y Y N Y Y N Y
Y N N Y Y N Y N N N N
predicted discrimination
But this is a latent response.
Use supervised LDA to predict bill discrimination from bill text.
90
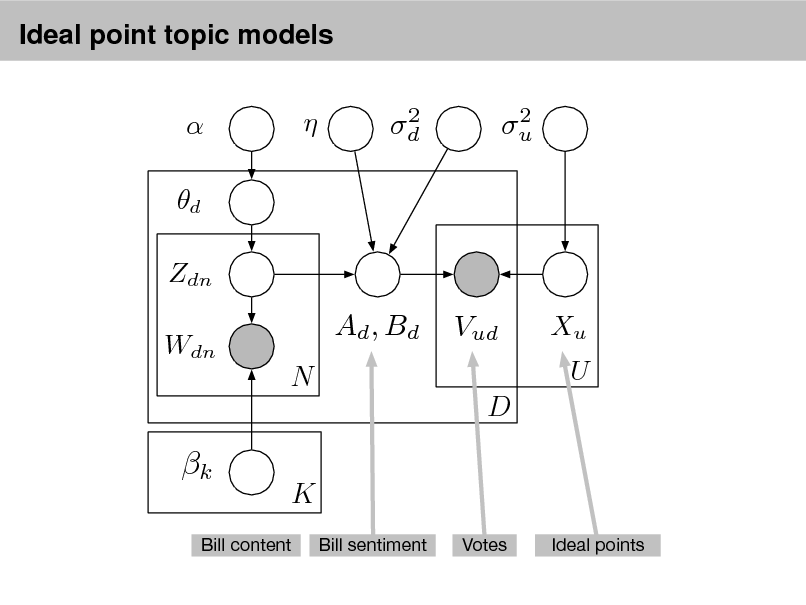
Ideal point topic models
d
Zdn Wdn
2 d
2 u
Ad , Bd
N
Vud
D
Xu U
k
K
Bill sentiment Votes Ideal points
Bill content
91
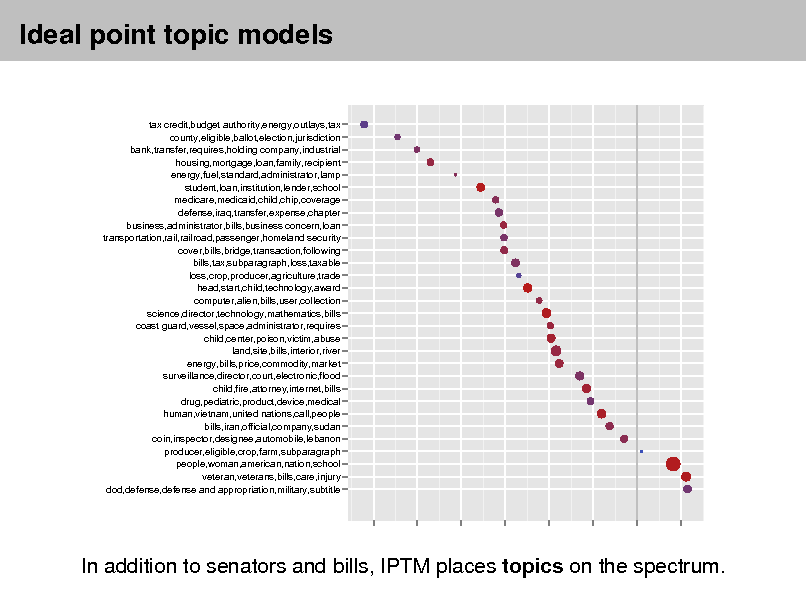
Ideal point topic models
tax credit,budget authority,energy,outlays,tax county,eligible,ballot,election,jurisdiction bank,transfer,requires,holding company,industrial housing,mortgage,loan,family,recipient energy,fuel,standard,administrator,lamp student,loan,institution,lender,school medicare,medicaid,child,chip,coverage defense,iraq,transfer,expense,chapter business,administrator,bills,business concern,loan transportation,rail,railroad,passenger,homeland security cover,bills,bridge,transaction,following bills,tax,subparagraph,loss,taxable loss,crop,producer,agriculture,trade head,start,child,technology,award computer,alien,bills,user,collection science,director,technology,mathematics,bills coast guard,vessel,space,administrator,requires child,center,poison,victim,abuse land,site,bills,interior,river energy,bills,price,commodity,market surveillance,director,court,electronic,flood child,fire,attorney,internet,bills drug,pediatric,product,device,medical human,vietnam,united nations,call,people bills,iran,official,company,sudan coin,inspector,designee,automobile,lebanon producer,eligible,crop,farm,subparagraph people,woman,american,nation,school veteran,veterans,bills,care,injury dod,defense,defense and appropriation,military,subtitle
In addition to senators and bills, IPTM places topics on the spectrum.
92

Summary: Supervised topic models
Many documents are associated with response variables. Supervised LDA embeds LDA in a generalized linear model that is
conditioned on the latent topic assignments.
Relational topic models use sLDA assumptions with pair-wise responses
to model networks of documents.
Ideal point topic models demonstrates how the response variables can
themselves be latent variables. In this case, they are used downstream in a model of legislative behavior.
(SLDA, the RTM, and others are implemented in the R package lda.)
93

Modeling User Data and Text
94

Topic models for recommendation (Wang and Blei, 2011)
In-matrix prediction
Users Maximum likelihood from incomplete data via the EM algorithm Conditional Random Fields Introduction to Variational Methods for Graphical Models The Mathematics of Statistical Machine Translation Topic Models for Recommendation
Papers
Out-of-matrix prediction
With new models, this can be used to
In many settings, we have information about how people use documents.
Help people nd documents that they are interested in Learn about what the documents mean to the people reading them Learn about the people reading (or voting on) the documents.
(We also saw this in ideal point topic models.)
95

Topic models for recommendation (Wang and Blei, 2011)
In-matrix prediction
Users Maximum likelihood from incomplete data via the EM algorithm Conditional Random Fields Introduction to Variational Methods for Graphical Models The Mathematics of Statistical Machine Translation Topic Models for Recommendation
Papers
Out-of-matrix prediction
Online communities of scientists allow for new ways of connecting
researchers to the research literature.
With collaborative topic models, we recommend scientic articles based
both on other scientists preferences and their content.
We can form both in-matrix and out-of-matrix predictions. We can learn
about which articles are important, and which are interdisciplinary.
96
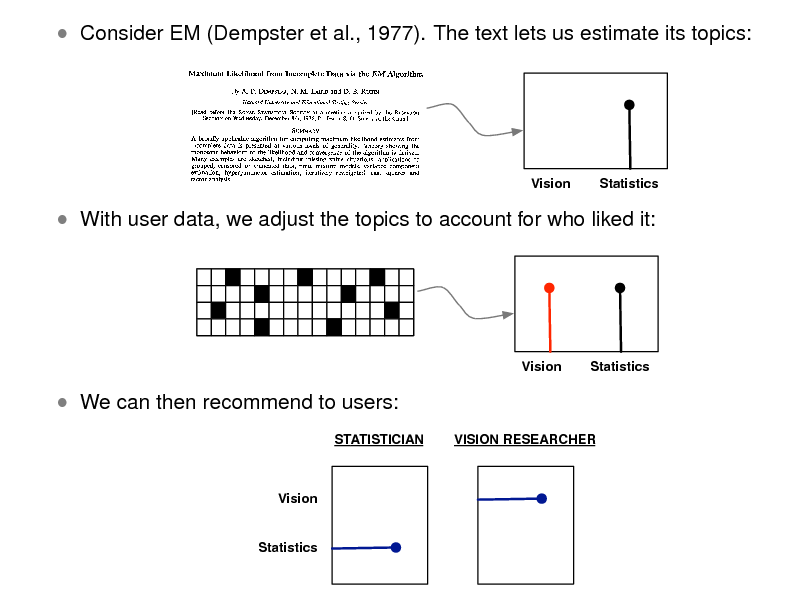
Consider EM (Dempster et al., 1977). The text lets us estimate its topics:
Vision
Statistics
With user data, we adjust the topics to account for who liked it:
Vision
Statistics
We can then recommend to users:
STATISTICIAN VISION RESEARCHER
Vision
Statistics
97
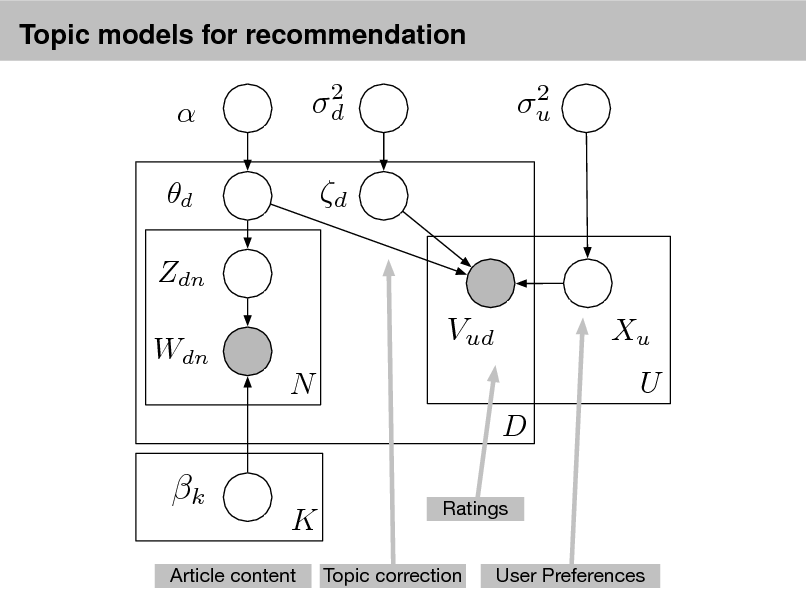
Topic models for recommendation
d
Zdn Wdn
2 d
2 u
d
Vud
N D
Xu U
k
K
Ratings Topic correction User Preferences
Article content
98

Topic models for recommendation
Big data set from Mendeley.com Fit the model with stochastic optimization The data
261K documents 80K users
10K vocabulary terms 25M observed words
5.1M entries (sparsity is 0.02%)
99

100
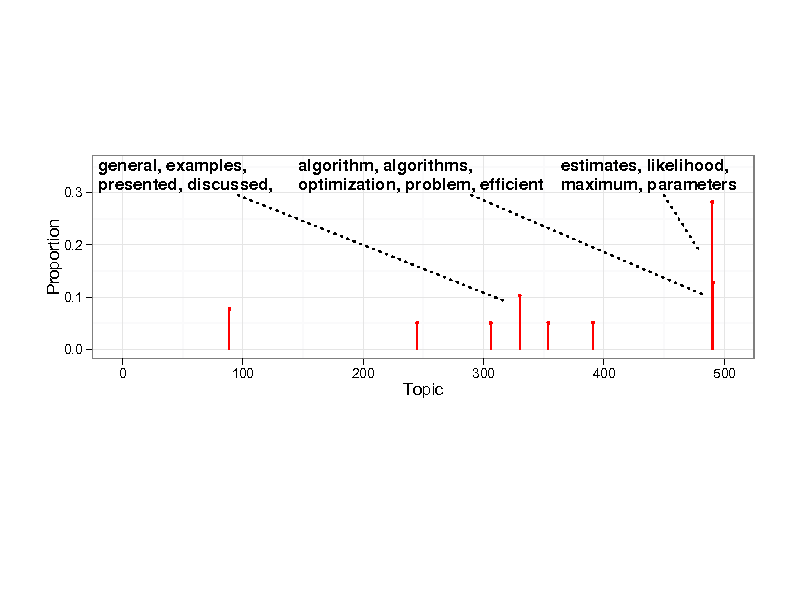
0.3
general, examples, presented, discussed,
algorithm, algorithms, optimization, problem, efcient
estimates, likelihood, maximum, parameters
Proportion
0.2
0.1
0.0 0 100 200
Topic
300
400
500
101
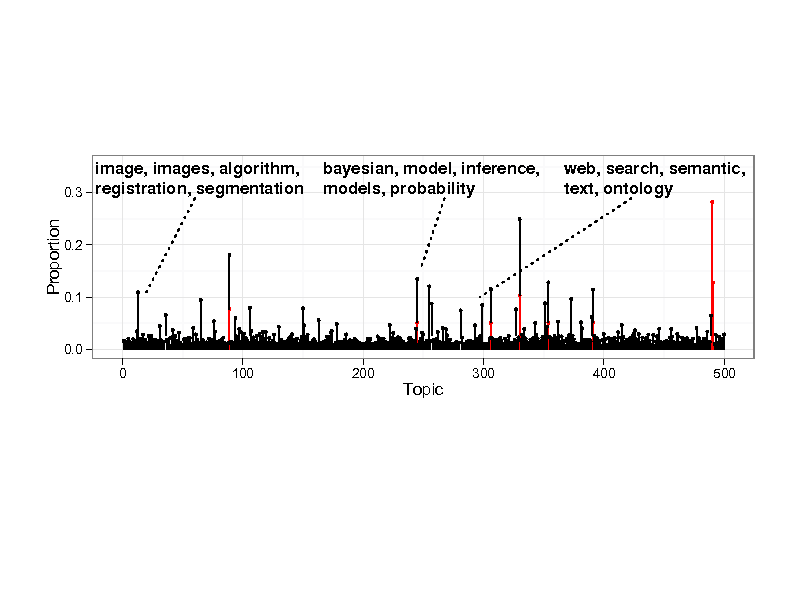
0.3
image, images, algorithm, registration, segmentation
bayesian, model, inference, models, probability
web, search, semantic, text, ontology
Proportion
0.2
0.1
0.0 0 100 200
Topic
300
400
500
102

103
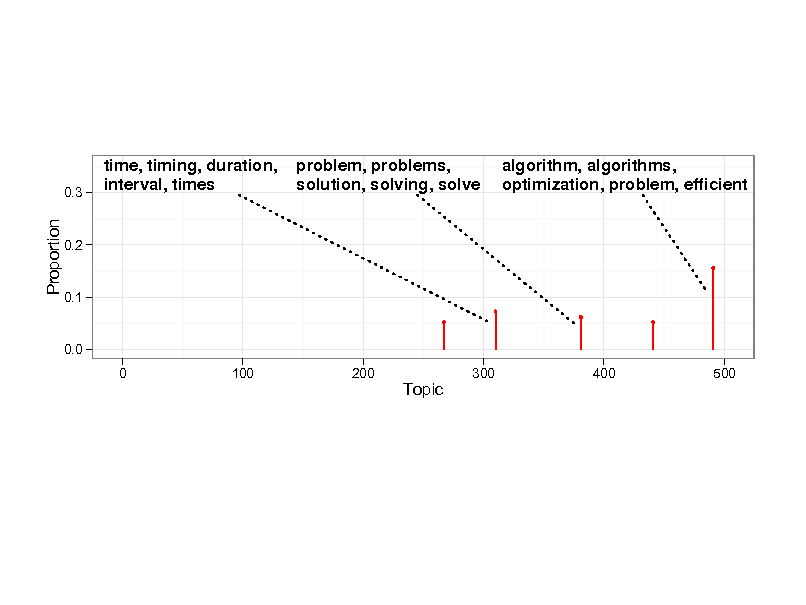
0.3
time, timing, duration, interval, times
problem, problems, solution, solving, solve
algorithm, algorithms, optimization, problem, efcient
Proportion
0.2
0.1
0.0 0 100 200
Topic
300
400
500
104
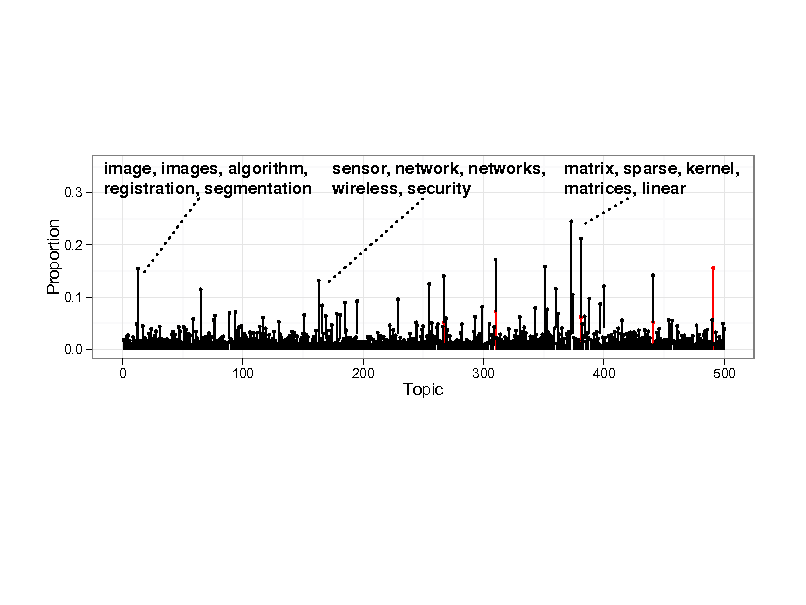
0.3
image, images, algorithm, registration, segmentation
sensor, network, networks, wireless, security
matrix, sparse, kernel, matrices, linear
Proportion
0.2
0.1
0.0 0 100 200
Topic
300
400
500
105
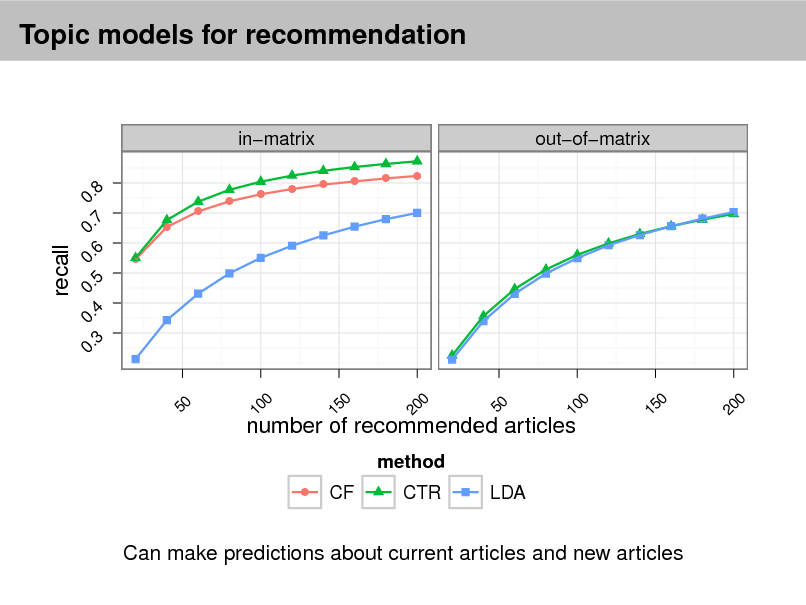
Topic models for recommendation
inmatrix
0. 0. 0. 0. 0. 4 5 6 7 8
q q q q q q
outofmatrix
q q q
q
recall
0.
3
0
0
0
0
0
50
10
15
20
50
10
15
number of recommended articles
method
q
CF
CTR
LDA
Can make predictions about current articles and new articles
20
0
106

More than recommendation
Maximum likelihood from incomplete data via the EM algorithm Conditional Random Fields Introduction to Variational Methods for Graphical Models The Mathematics of Statistical Machine Translation
Papers
The users also tell us about the data. We can look at posterior estimates to nd
Widely read articles in a eld Articles in a eld that are widely read in other elds
Articles from other elds that are widely read in a eld
These kinds of explorations require interpretable dimensions.
They are not possible with classical matrix factorization.
107
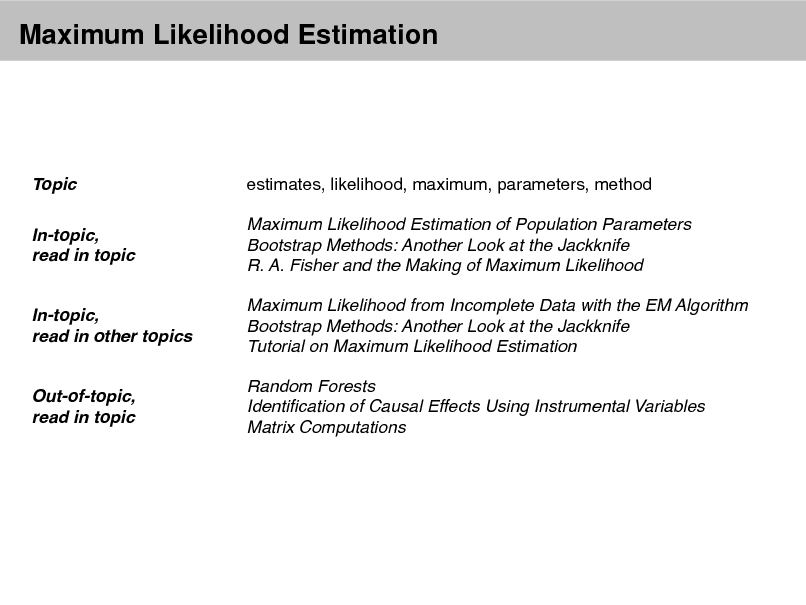
Maximum Likelihood Estimation
Topic In-topic, read in topic
estimates, likelihood, maximum, parameters, method Maximum Likelihood Estimation of Population Parameters Bootstrap Methods: Another Look at the Jackknife R. A. Fisher and the Making of Maximum Likelihood Maximum Likelihood from Incomplete Data with the EM Algorithm Bootstrap Methods: Another Look at the Jackknife Tutorial on Maximum Likelihood Estimation Random Forests Identication of Causal Effects Using Instrumental Variables Matrix Computations
In-topic, read in other topics
Out-of-topic, read in topic
108
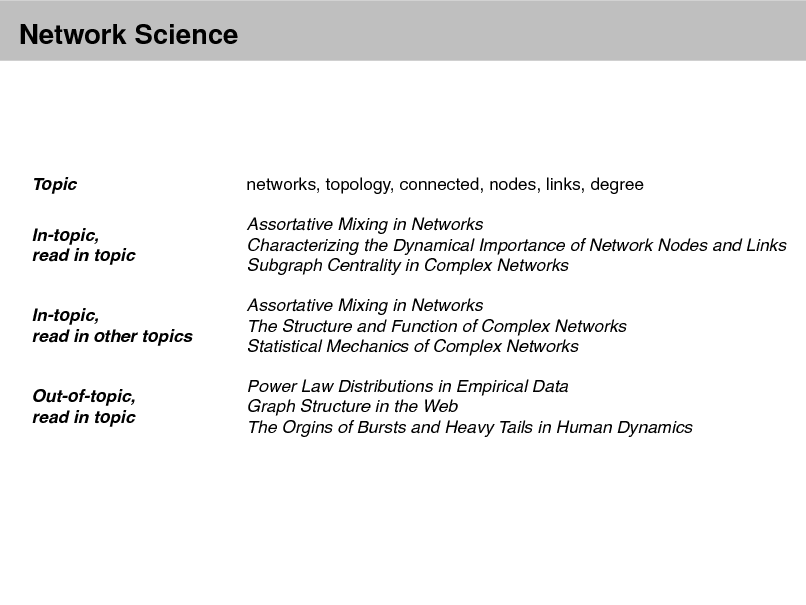
Network Science
Topic In-topic, read in topic
networks, topology, connected, nodes, links, degree Assortative Mixing in Networks Characterizing the Dynamical Importance of Network Nodes and Links Subgraph Centrality in Complex Networks Assortative Mixing in Networks The Structure and Function of Complex Networks Statistical Mechanics of Complex Networks Power Law Distributions in Empirical Data Graph Structure in the Web The Orgins of Bursts and Heavy Tails in Human Dynamics
In-topic, read in other topics
Out-of-topic, read in topic
109

Issue-adjusted ideal points
Our earlier ideal point model uses topics to predict votes from new bills.
from their usual ideal points. comes to economic matters.
Alternatively, we can use the text to characterize how legislators diverge For example: A senator might be left wing, but vote conservatively when it
110
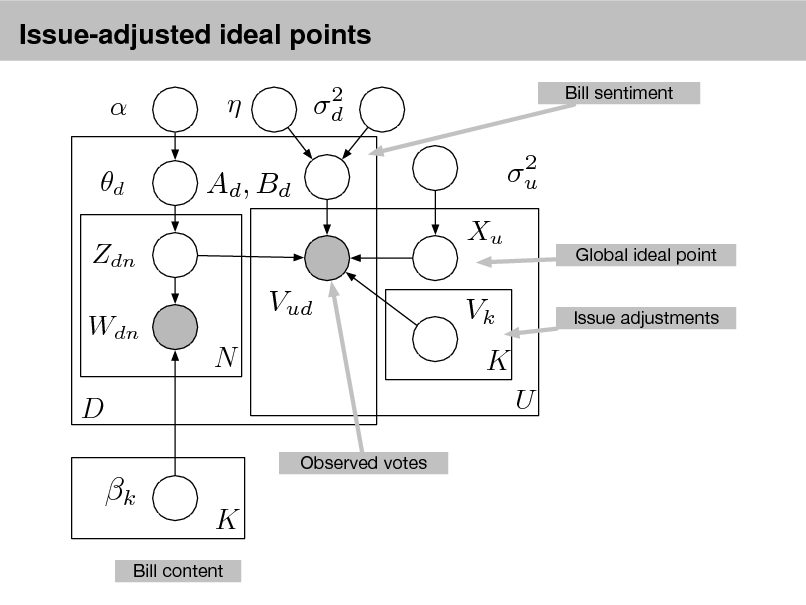
Issue-adjusted ideal points
d
Zdn Wdn
2 d 2 u
Bill sentiment
Ad , Bd
Xu
Global ideal point Issue adjustments
Vud
N
Vk
K
U
D
Observed votes
k
K
Bill content
111
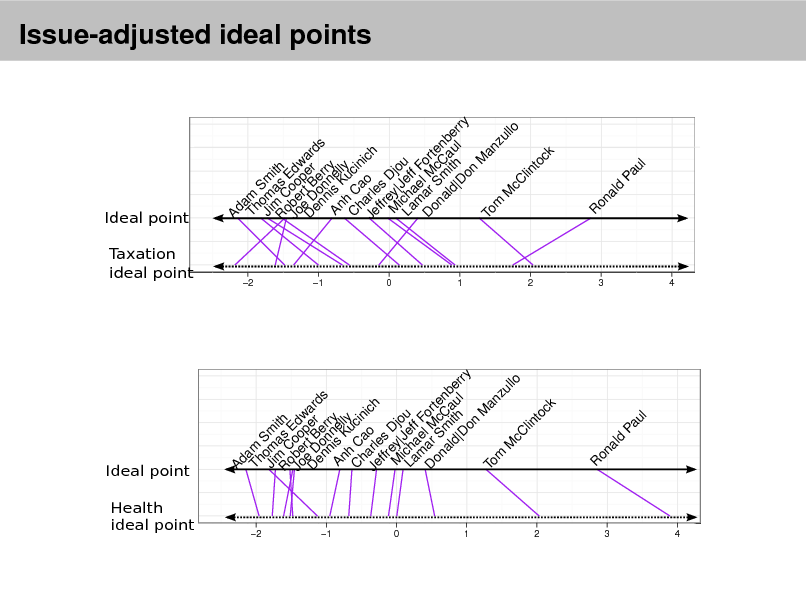
Ideal point
Ideal point
Taxation ideal point
Issue-adjusted ideal points
Health ideal point
2
2
1
1 0 1 2 3 4
0 1 2 3 4
Ad Tham Ji om Sm R m Cas ith o Jo be oo Edw p D e Drt B er ard en o e s n n rr An is nel y h K ly C C ucin h a Je arle o ich ffr s M ey| Djo Laich Jef u m ae f F D ar l M or t on S c e al mi Ca nb d| th u er l ry D on M To an m zu M llo cC lin to ck R
on
al
d
Pa u
l
112

Extending LDA
New applications
Syntactic topic models
Topic models on images
Topic models on social network data Topic models on music data Topic models for recommendation systems
Testing and relaxing assumptions
Spike and slab priors N-gram topic models
Models of word contagion
113
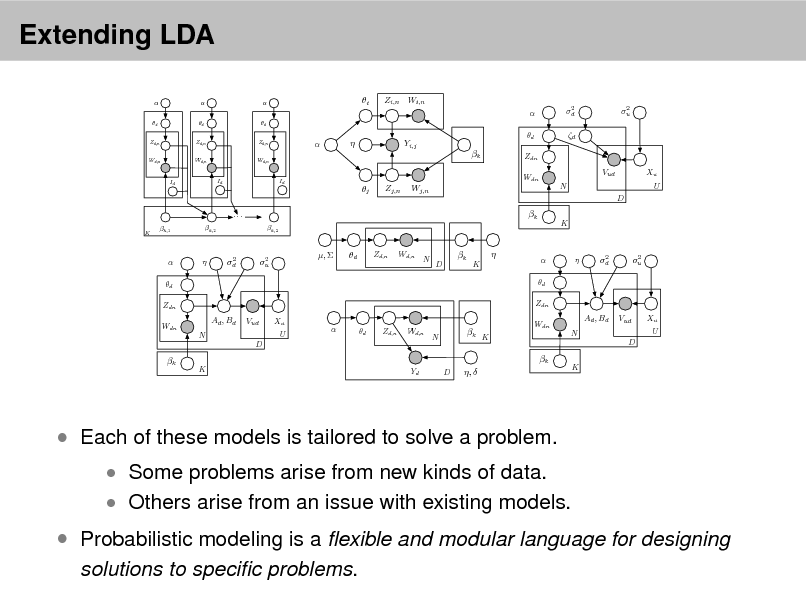
Extending LDA
d Zd,n Wd,n d Zd,n Wd,n d Zd,n Wd,n
i
Zi,n Wi,n
d
2 d
2 u
Yi,j
d
k
Id
Zdn Wdn
Vud
N D
Xu U
Id
Id
j
Zj,n
Wj,n
...
K
k
k,2
k,1
k,2
K
d
Zdn Wdn
2 d
2 u
,
d
Zd,n
Wd,n
N
D
k
K
d
Zdn
2 d
2 u
Ad , Bd
N
Vud
D
Xu U
d
Zd,n
Wd,n
N
k K
Wdn
Ad , Bd
N
Vud
D
Xu U
k
k
K
Yd
D
,
K
Each of these models is tailored to solve a problem.
Some problems arise from new kinds of data. Others arise from an issue with existing models.
Probabilistic modeling is a exible and modular language for designing
solutions to specic problems.
114
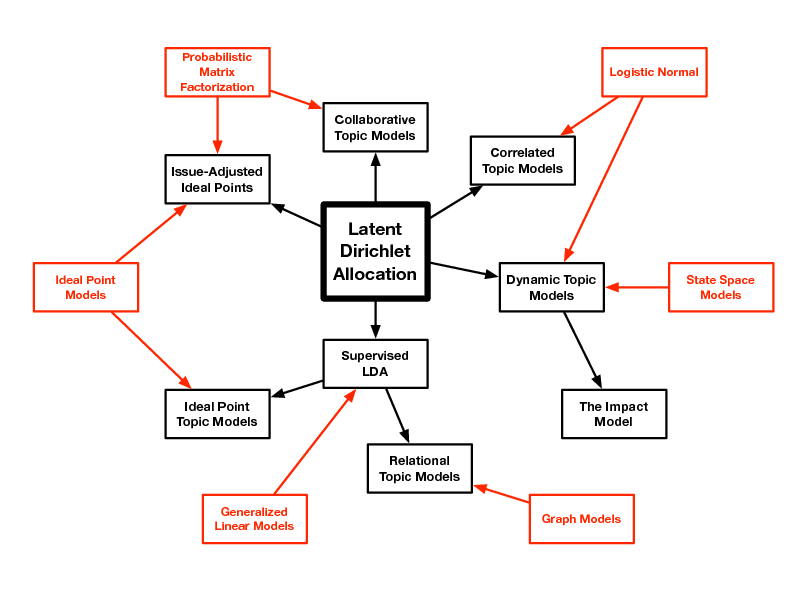
Probabilistic Matrix Factorization
Logistic Normal
Collaborative Topic Models Issue-Adjusted Ideal Points Correlated Topic Models
Ideal Point Models
Latent Dirichlet Allocation
Dynamic Topic Models
State Space Models
Supervised LDA Ideal Point Topic Models Relational Topic Models
Generalized Linear Models Graph Models
The Impact Model
115
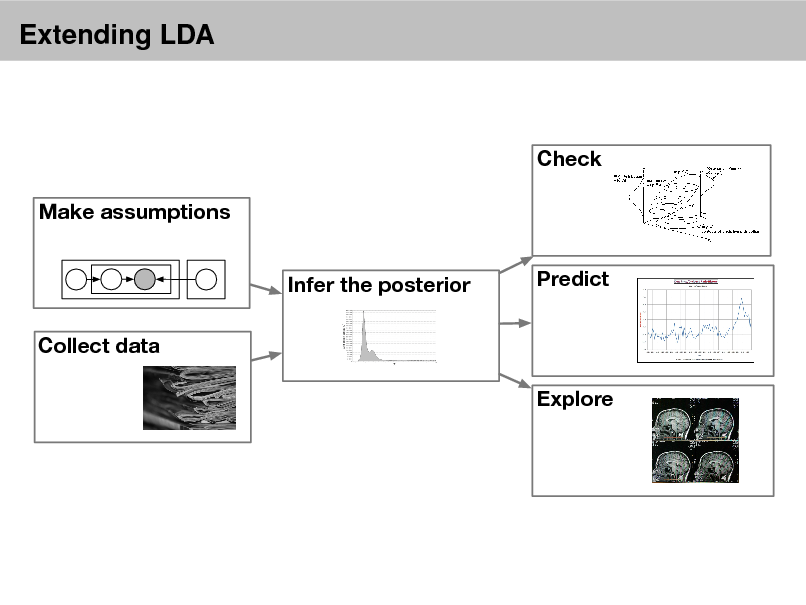
Extending LDA
Check Make assumptions Infer the posterior Collect data Explore Predict
116

Bayesian Nonparametric Models
117

Bayesian nonparametric models
Why Bayesian nonparametric models? The Chinese restaurant process Chinese restaurant process mixture models The Chinese restaurant franchise Bayesian nonparametric topic models
Random measures and stick-breaking constructions
118

Why Bayesian nonparametric models?
Topic models assume that the number of topics is xed. It is a type of regularization parameter. It can be determined by cross
validation and other model selection techniques.
Bayesian nonparametric methods skirt model selection
The data determine the number of topics during inference. Future data can exhibit new topics.
(This is a eld unto itself, but has found wide application in topic modeling.)
119
The Chinese restaurant process (CRP)
1 3 4
8
2
6
7
9
5
10
N customers arrive to an innite-table restaurant. Each sits down according
to how many people are sitting at each table, p(zi = k | z1:(i 1) , ) nk
for k K for k = K + 1.
The resulting seating plan provides a partition This distribution is exchangeable: Seating plan probabilities are the same
regardless of the order of customers (Pitman, 2002).
120
CRP mixture models
1 3 4
8
2
6
7
1
5
2
10
3
4
9
5
Associate each table with a topic ( ).
Associate each customer with a data point (grey node).
The number of clusters is innite a priori;
the data determines the number of clusters in the posterior.
Further: the next data point might sit at new table. Exchangeability makes inference easy (Escobar and West, 1995; Neal, 2000).
121
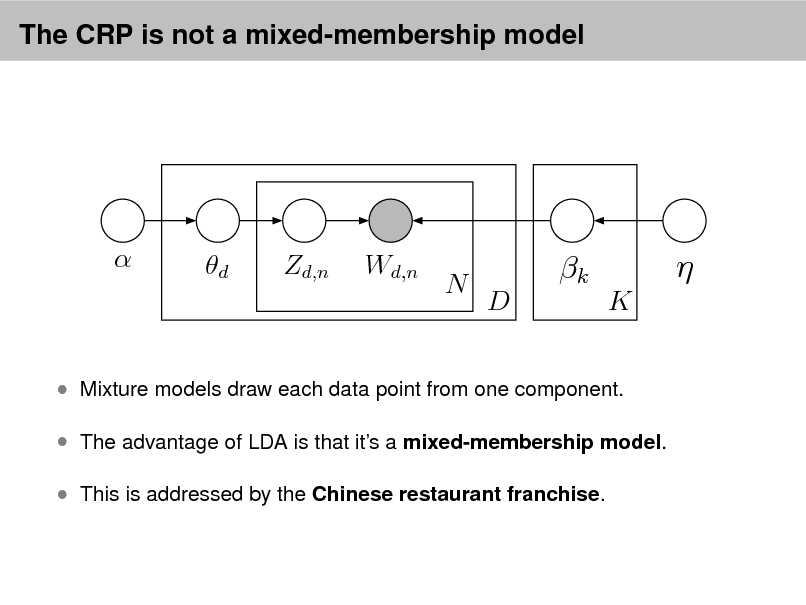
The CRP is not a mixed-membership model
d
Zd,n
Wd,n
N
k
D K
Mixture models draw each data point from one component. The advantage of LDA is that its a mixed-membership model. This is addressed by the Chinese restaurant franchise.
122
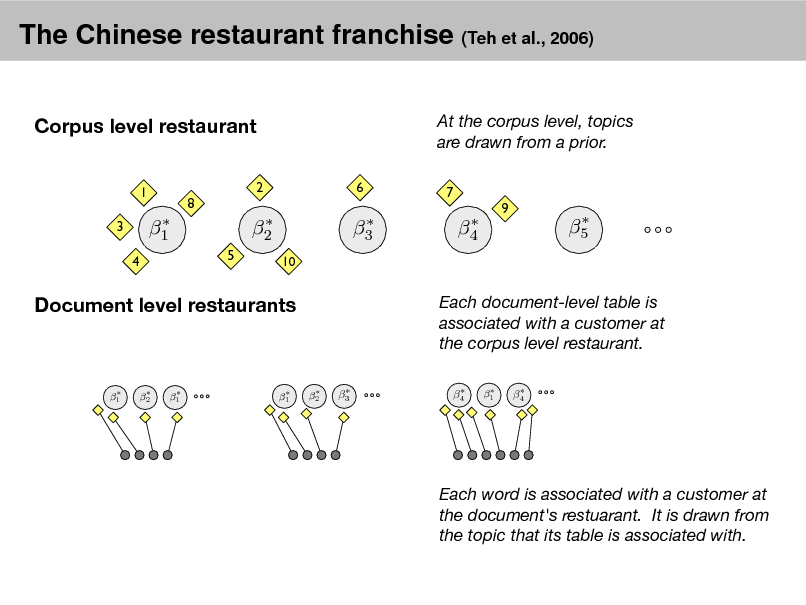
The Chinese restaurant franchise (Teh et al., 2006)
Corpus level restaurant
1 3 4 2 6
At the corpus level, topics are drawn from a prior.
7
8
1
5
2
10
3
4
9
5
Document level restaurants
Each document-level table is associated with a customer at the corpus level restaurant.
2
1
2
1
1
3
4
1
4
Each word is associated with a customer at the document's restuarant. It is drawn from the topic that its table is associated with.
123
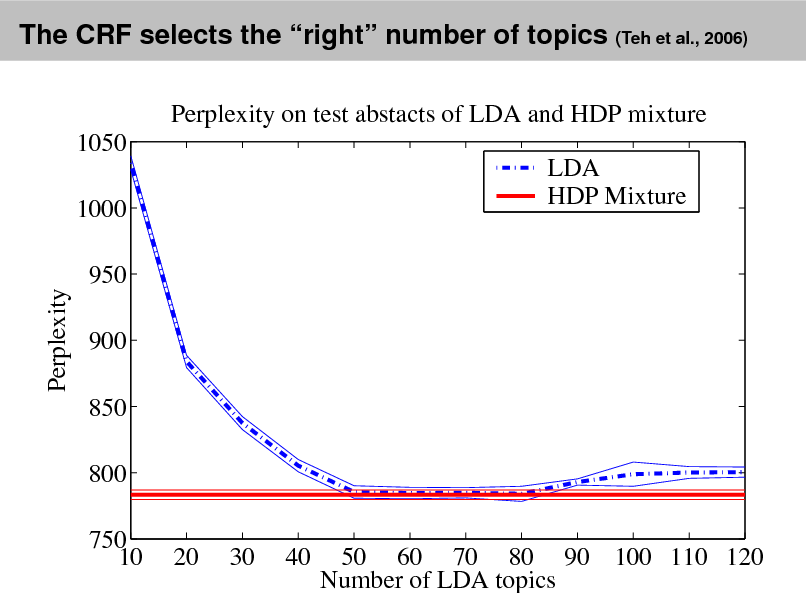
The CRF selects the right number of topics (Teh et al., 2006)
Perplexity on test abstacts of LDA and HDP mixture 1050 1000 950 900 850 800 750 10 20 30 40 50 60 70 80 90 100 110 120 Number of LDA topics LDA HDP Mixture
Perplexity
124
Extended to nd hierarchies (Blei et al., 2010)
online scheduling task competitive tasks
Quantum lower bounds by polynomials On the power of bounded concurrency I: finite automata Dense quantum coding and quantum finite automata Classical physics and the Church--Turing Thesis
quantum automata nc automaton languages
approximation s points distance convex routing adaptive network networks protocols
Nearly optimal algorithms and bounds for multilayer channel routing How bad is selfish routing? Authoritative sources in a hyperlinked environment Balanced sequences and optimal routing
machine domain degree degrees polynomials
n functions polynomial log algorithm
networks protocol network packets link
An optimal algorithm for intersecting line segments in the plane Recontamination does not help to search a graph A new approach to the maximum-flow problem The time complexity of maximum matching by simulated annealing
graph graphs edge minimum vertices
learning learnable statistical examples classes
the,of a, is and
n algorithm time log bound logic programs systems language sets
m merging networks sorting multiplication
database constraints algebra boolean relational
constraint dependencies local consistency tractable
Module algebra On XML integrity constraints in the presence of DTDs Closure properties of constraints Dynamic functional dependencies and database aging
logic logics query theories languages
consensus objects messages protocol asynchronous
system systems performance analysis distributed
learning knowledge reasoning verication circuit
trees regular tree search compression
Magic Functions: In Memoriam: Bernard M. Dwork 1923--1998 A mechanical proof of the Church-Rosser theorem Timed regular expressions On the power and limitations of strictness analysis
proof property program resolution abstract
formulas rstorder decision temporal queries
database transactions retrieval concurrency restrictions
networks queuing asymptotic productform server
Single-class bounds of multi-class queuing networks The maximum concurrent flow problem Contention in shared memory algorithms Linear probing with a nonuniform address distribution
125

BNP correlated topic model (Paisley et al., 2011)
{president party elect}
{military army armed} {colony {international china union} slave independence}
{law convention international}
{william lord earl}
{kill prisoner arrest}
{county home population}
{film award director}
{empire ottoman territory} {son father brother} {emperor reign imperial}
{host centre football}
{publish story publication}
{report fbi investigation}
{battle army {island ship islands} fight}
{student university school} {jersey york uniform}
{album song music}
{church catholic roman}
{calendar month holiday} {site town wall}
{university prize {law legal court}
award}
{film scene movie} {company car engine} {game sell video}
{language culture spanish}
{population female male}
{art painting socialism {capitalist artist}
capitalism}
{universe destroy series}
{political society argue}
{building wall design}
{game {weapon gun design} player character} {technology information organization}
{god greek ancient}
{sport competition {music instrument musical}
event}
{social theory cultural} {language letter sound} {noun verb language} {heat pressure mechanical}
{mathematician numeral decimal}
{earth relativity} {motion law planet solar}
{water sub metal}
{wave light field}
{math function define}
126
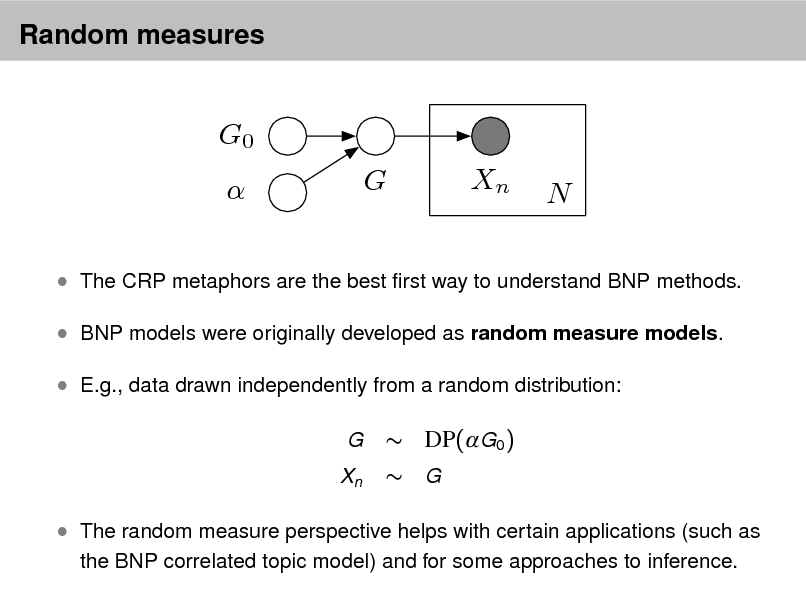
Random measures
G0 G Xn N
The CRP metaphors are the best rst way to understand BNP methods. BNP models were originally developed as random measure models. E.g., data drawn independently from a random distribution:
G Xn
DP(G0 ) G
The random measure perspective helps with certain applications (such as
the BNP correlated topic model) and for some approaches to inference.
127
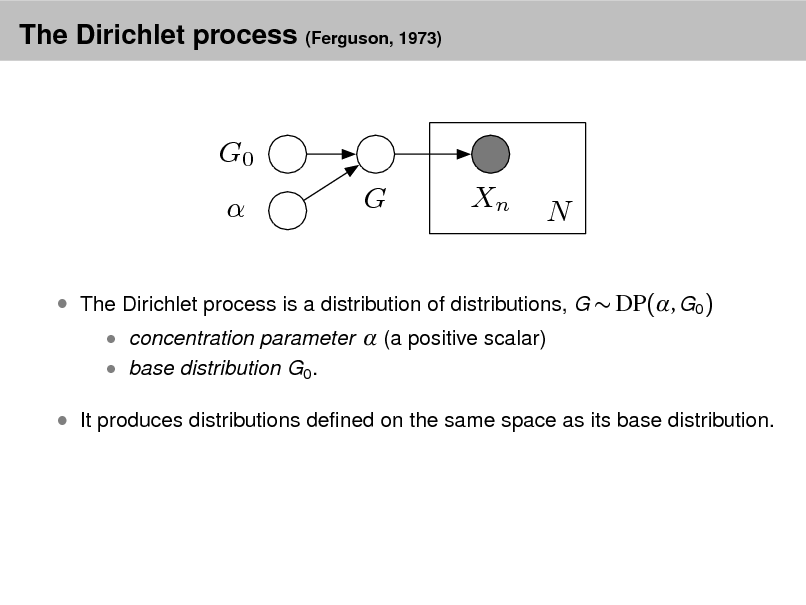
The Dirichlet process (Ferguson, 1973)
G0 G Xn N
The Dirichlet process is a distribution of distributions, G DP(, G0 )
concentration parameter (a positive scalar) base distribution G0 .
It produces distributions dened on the same space as its base distribution.
128
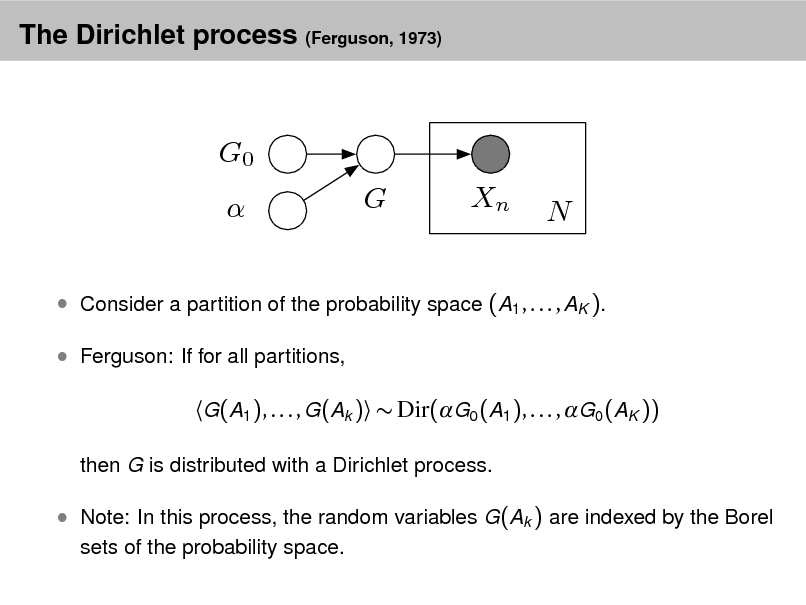
The Dirichlet process (Ferguson, 1973)
G0 G Xn N
Consider a partition of the probability space (A1 , . . . , AK ). Ferguson: If for all partitions,
G(A1 ), . . . , G(Ak ) Dir(G0 (A1 ), . . . , G0 (AK ))
then G is distributed with a Dirichlet process.
Note: In this process, the random variables G(Ak ) are indexed by the Borel
sets of the probability space.
129
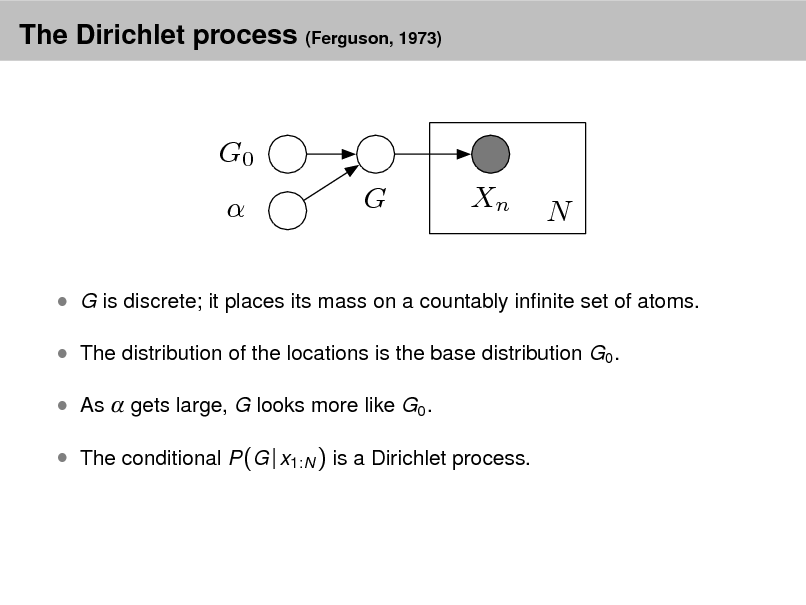
The Dirichlet process (Ferguson, 1973)
G0 G Xn N
G is discrete; it places its mass on a countably innite set of atoms. The distribution of the locations is the base distribution G0 . As gets large, G looks more like G0 . The conditional P (G | x1:N ) is a Dirichlet process.
130
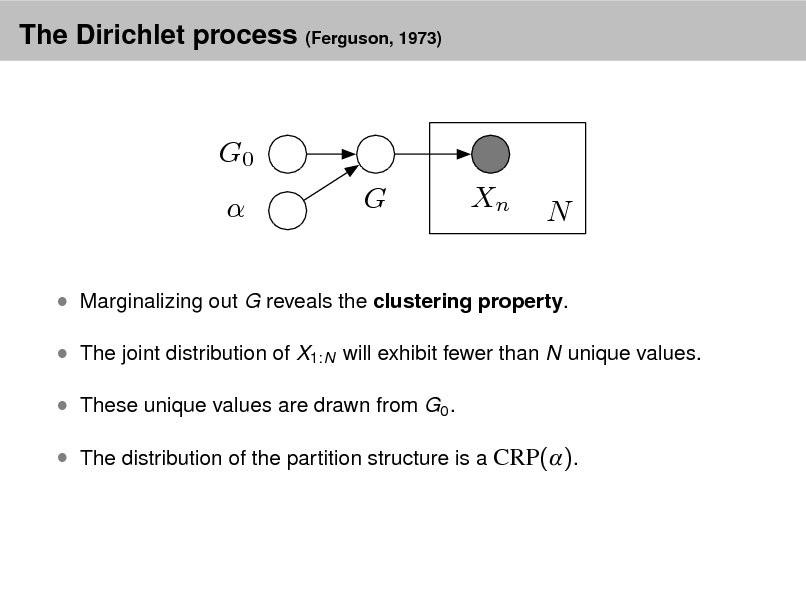
The Dirichlet process (Ferguson, 1973)
G0 G Xn N
Marginalizing out G reveals the clustering property. The joint distribution of X1:N will exhibit fewer than N unique values. These unique values are drawn from G0 . The distribution of the partition structure is a CRP().
131
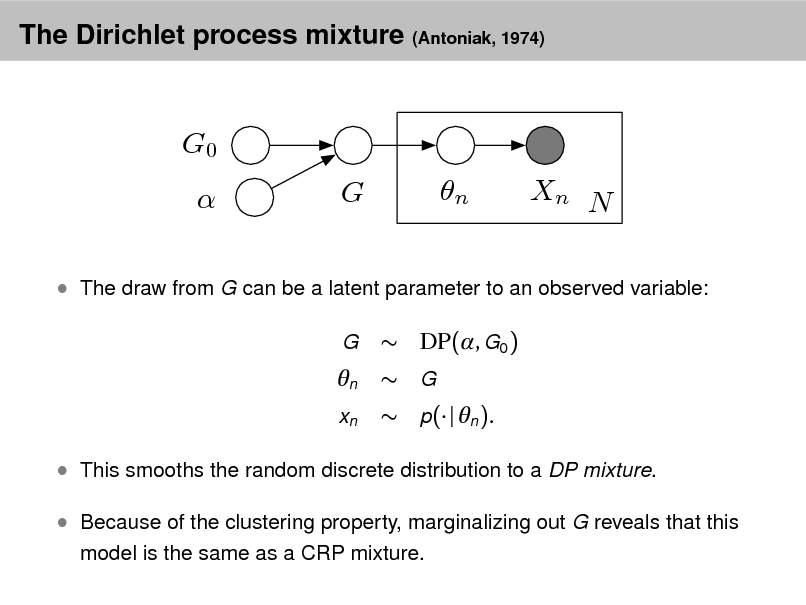
The Dirichlet process mixture (Antoniak, 1974)
G0 G n Xn N
The draw from G can be a latent parameter to an observed variable:
G
DP(, G0 ) G p( | n ).
n
xn
This smooths the random discrete distribution to a DP mixture. Because of the clustering property, marginalizing out G reveals that this
model is the same as a CRP mixture.
132
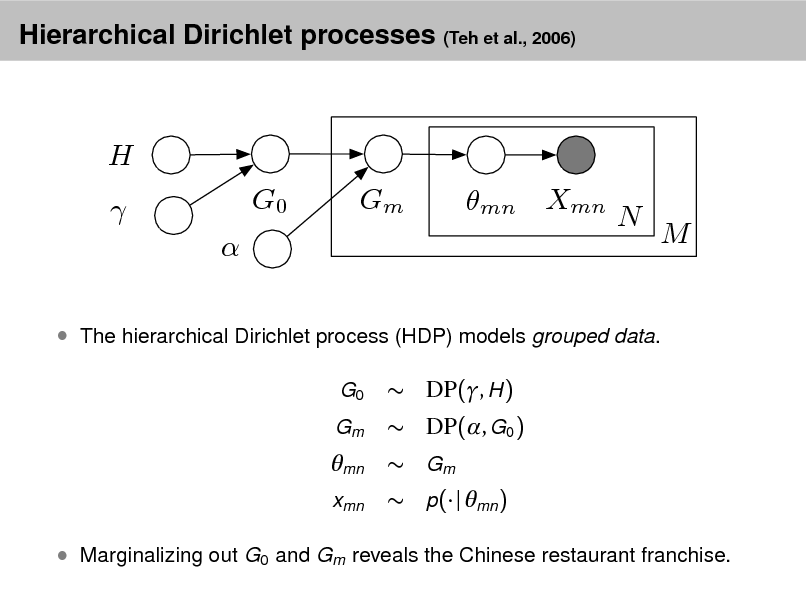
Hierarchical Dirichlet processes (Teh et al., 2006)
H G0 Gm mn Xmn N M
The hierarchical Dirichlet process (HDP) models grouped data.
G0 Gm
DP(, H ) DP(, G0 ) Gm p( | mn )
mn
xmn
Marginalizing out G0 and Gm reveals the Chinese restaurant franchise.
133
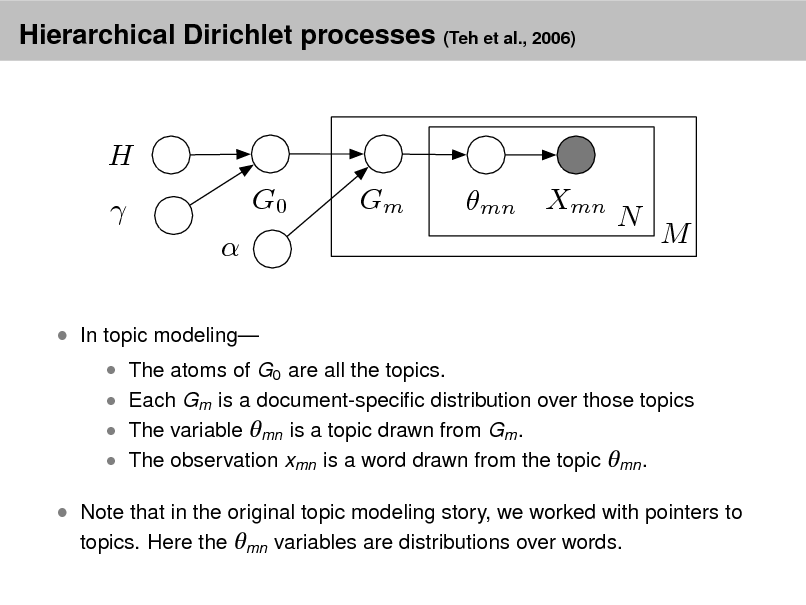
Hierarchical Dirichlet processes (Teh et al., 2006)
H
In topic modeling
G0
Gm
mn Xmn
N
M
The atoms of G0 are all the topics. Each Gm is a document-specic distribution over those topics The variable mn is a topic drawn from Gm . The observation xmn is a word drawn from the topic mn .
Note that in the original topic modeling story, we worked with pointers to topics. Here the mn variables are distributions over words.
134

Summary: Bayesian nonparametrics
Bayesian nonparametric modeling is a growing eld (Hjort et al., 2011). BNP methods can dene priors over latent combinatorial structures. In the posterior, the documents determine the particular form of the
structure that is best for the corpus at hand.
Recent innovations:
Improved inference (Blei and Jordan, 2006, Wang et al. 2011) BNP models for language (Teh, 2006; Goldwater et al., 2011) Dependent models, such as time series models
(MacEachern 1999, Dunson 2010, Blei and Frazier 2011)
Predictive models (Hannah et al. 2011) Factorization models (Grifths and Ghahramani, 2011)
135

Posterior Inference
136
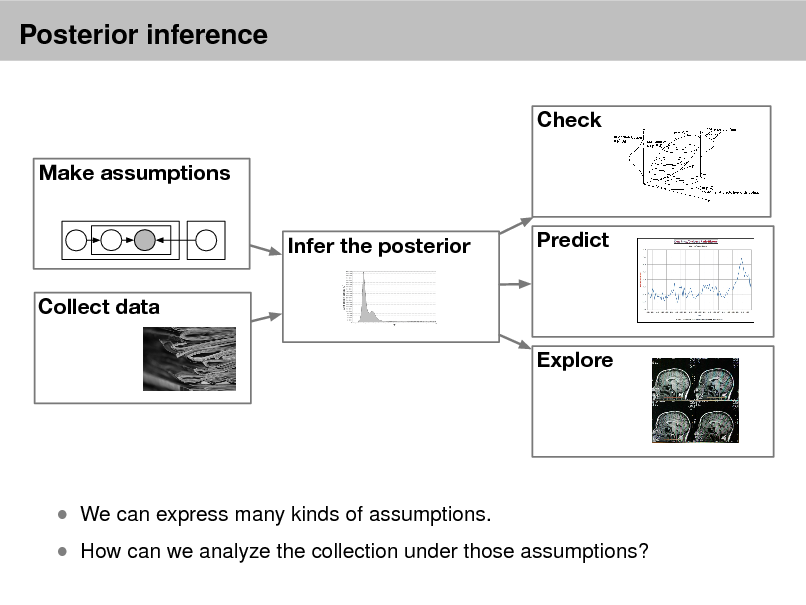
Posterior inference
Check Make assumptions Infer the posterior Collect data Explore Predict
How can we analyze the collection under those assumptions?
We can express many kinds of assumptions.
137
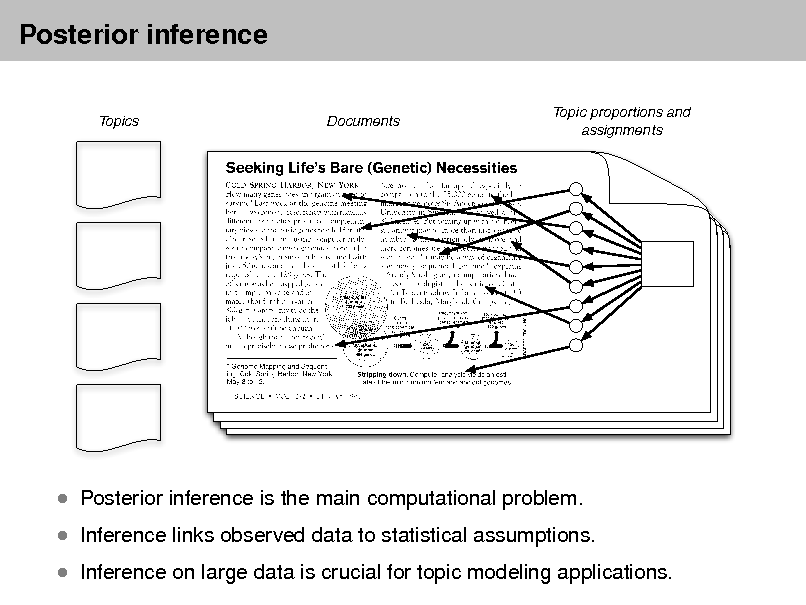
Posterior inference
Topics Documents Topic proportions and assignments
Inference links observed data to statistical assumptions.
Posterior inference is the main computational problem.
Inference on large data is crucial for topic modeling applications.
138
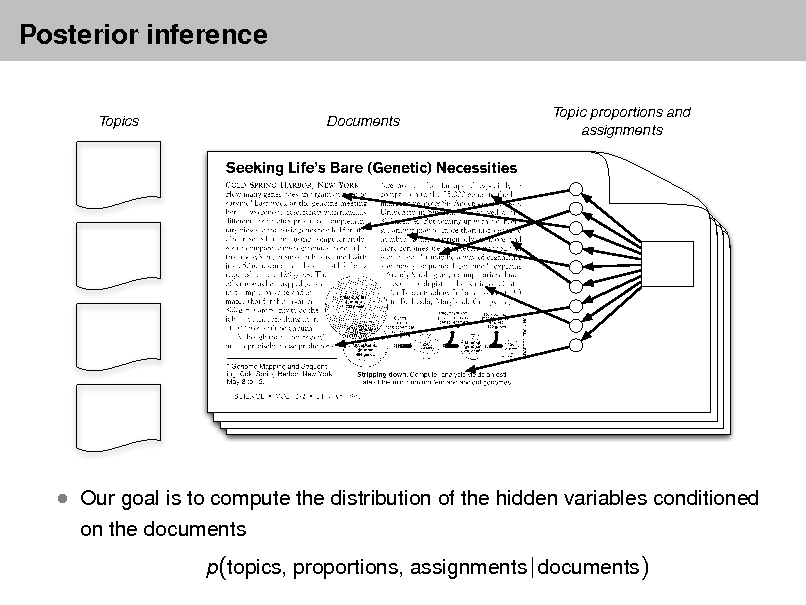
Posterior inference
Topics Documents Topic proportions and assignments
Our goal is to compute the distribution of the hidden variables conditioned
on the documents p(topics, proportions, assignments | documents)
139
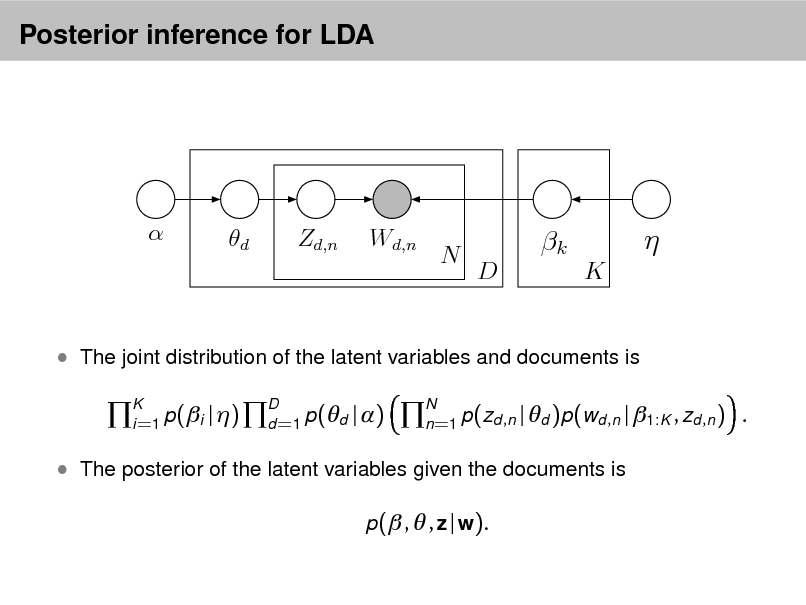
Posterior inference for LDA
d
Zd,n
Wd,n
N
k
D K
The joint distribution of the latent variables and documents is
K p(i i =1
| )
D p(d d =1
| )
N p(zd ,n | d )p(wd ,n | 1:K , zd ,n ) n=1
.
The posterior of the latent variables given the documents is
p( , , z | w).
140
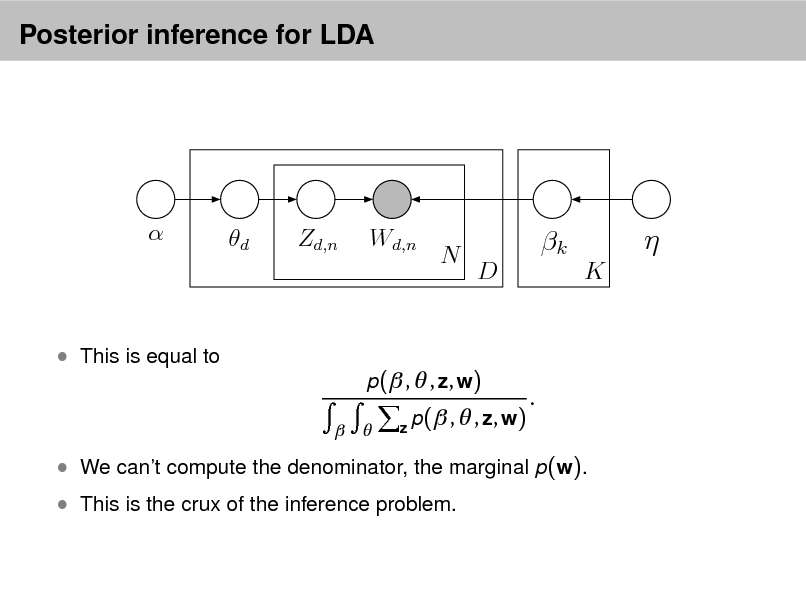
Posterior inference for LDA
d
Zd,n
Wd,n
N
k
D K
This is equal to
p( , , z, w)
z p ( , , z, w)
.
We cant compute the denominator, the marginal p(w). This is the crux of the inference problem.
141
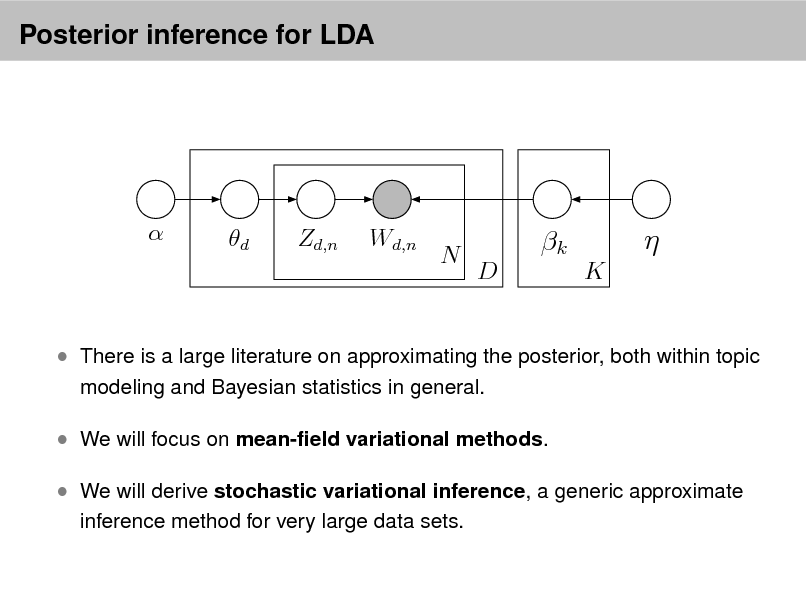
Posterior inference for LDA
d
Zd,n
Wd,n
N
k
D K
There is a large literature on approximating the posterior, both within topic
modeling and Bayesian statistics in general.
We will focus on mean-eld variational methods. We will derive stochastic variational inference, a generic approximate
inference method for very large data sets.
142

Variational inference
Variational inference turns posterior inference into optimization. The main idea
Place a distribution over the hidden variables with free parameters,
called variational parameters.
Optimize the variational parameters to make the distribution close (in
KL divergence) to the true posterior
Variational inference can be faster than sampling-based approaches. It is easier to handle nonconjugate models with variational inference.
(This is important in the CTM, DTM, and legislative models.)
It can be scaled up to very large data sets with stochastic optimization.
143

Stochastic variational inference
We want to condition on large data sets and approximate the posterior. In variational inference, we optimize over a family of distributions to nd
the member closest in KL divergence to the posterior.
Variational inference usually results in an algorithm like this:
Infer local variables for each data point. Based on these local inferences, re-infer global variables. Repeat.
144

Stochastic variational inference
This is inefcient. We should know something about the global structure
after seeing part of the data.
And, it assumes a nite amount of data. We want algorithms that can
handle data sources, information arriving in a constant stream.
With stochastic variational inference, we can condition on large data and
approximate the posterior of complex models.
145

Stochastic variational inference
The structure of the algorithm is:
Subsample the dataone data point or a small batch. Infer local variables for the subsample.
Update the current estimate of the posterior of the global variables. Repeat.
This is efcientwe need only process one data point at a time. We will show: Just as easy as classical variational inference
146

Stochastic variational inference for LDA
Sample one document
Analyze it
Update the model
1 2 3 4 5
Sample a document wd from the collection Infer how wd exhibits the current topics Create intermediate topics, formed as though the wd is the only document. Adjust the current topics according to the intermediate topics. Repeat.
147
Stochastic variational inference for LDA
900 850 800 750 700 650 600
Online 98K
Perplexity
Online 3.3M
Batch 98K
103.5
Documents analyzed 2048 4096
Documents seen (log scale)
8192 12288 16384
104
104.5
105
105.5
32768
106
49152
106.5
65536
Top eight words
systems systems service road health systems made communication health service service companies announced billion market national language communication west care company language road billion
service service business business business systems companies service service industry companies systems companies companies service business business industry industry companies company company company services services billion industry management company company health market systems management management industry billion services public public
148
Stochastic variational inference for LDA
Sample one document
Analyze it
Update the model
We have developed stochastic variational inference algorithms for
The hierarchical Dirichlet process
Latent Dirichlet allocation
The discrete innite logistic normal
Mixed-membership stochastic blockmodels Bayesian nonparametric factor analysis Recommendation models and legislative models
149

Organization
Describe a generic class of models
Derive mean-eld variational inference in this class Review stochastic optimization
Derive natural gradients for the variational objective Derive stochastic variational inference
150
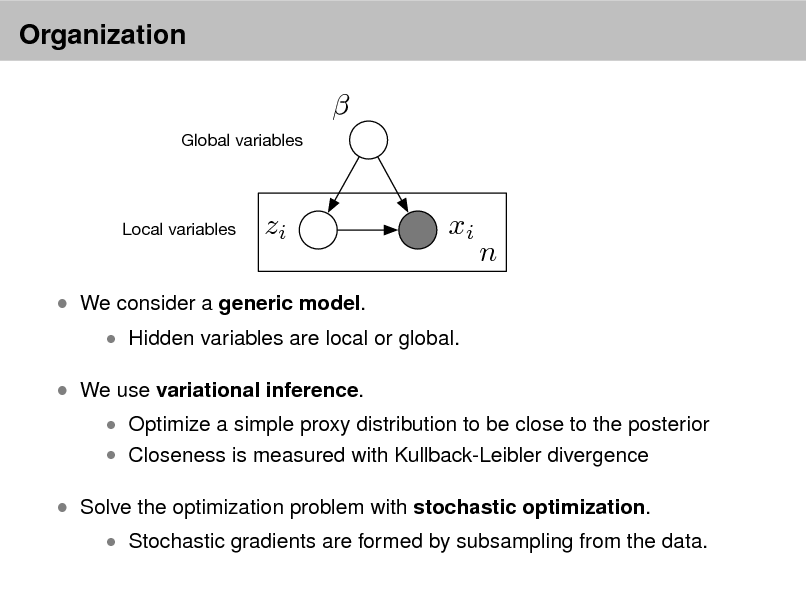
Organization
Global variables
Local variables
zi
xi
n
We consider a generic model. We use variational inference.
Hidden variables are local or global.
Optimize a simple proxy distribution to be close to the posterior Closeness is measured with Kullback-Leibler divergence
Solve the optimization problem with stochastic optimization.
Stochastic gradients are formed by subsampling from the data.
151
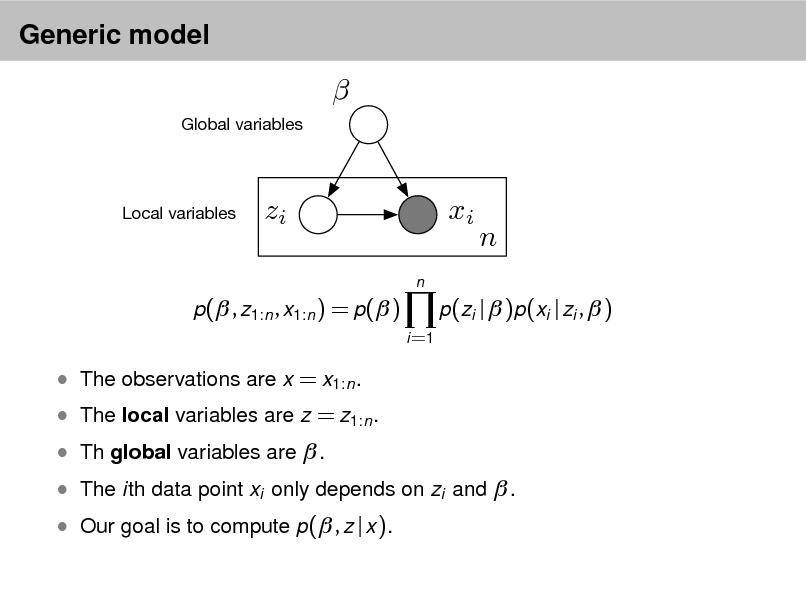
Generic model
Global variables
Local variables
zi
n
xi
n
p( , z1:n , x1:n ) = p( )
i =1
p(zi | )p(xi | zi , )
The observations are x = x1:n . Th global variables are .
The local variables are z = z1:n .
The ith data point xi only depends on zi and . Our goal is to compute p( , z | x ).
152
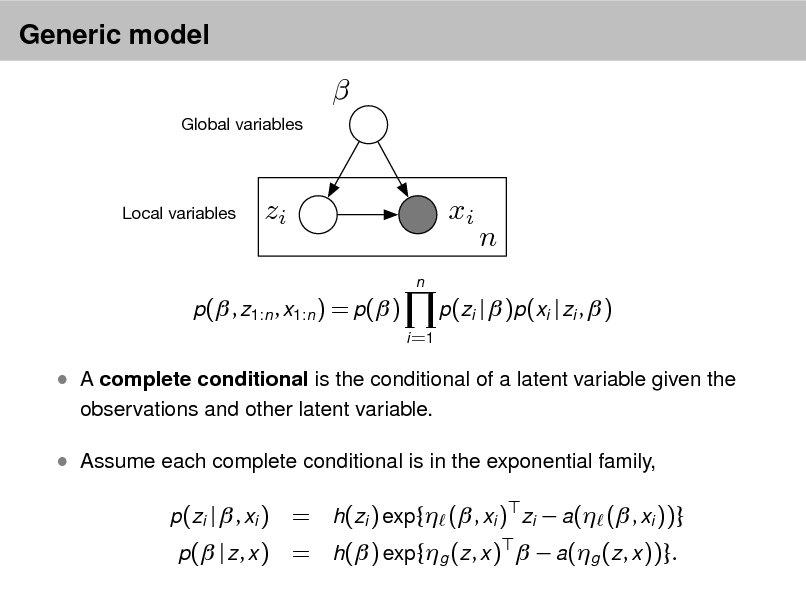
Generic model
Global variables
Local variables
zi
n
xi
n
p( , z1:n , x1:n ) = p( )
i =1
p(zi | )p(xi | zi , )
A complete conditional is the conditional of a latent variable given the
observations and other latent variable.
Assume each complete conditional is in the exponential family,
p(zi | , xi ) p( | z , x )
= h(zi ) exp{ ( , xi ) zi a( ( , xi ))} = h( ) exp{g (z , x ) a(g (z , x ))}.
153
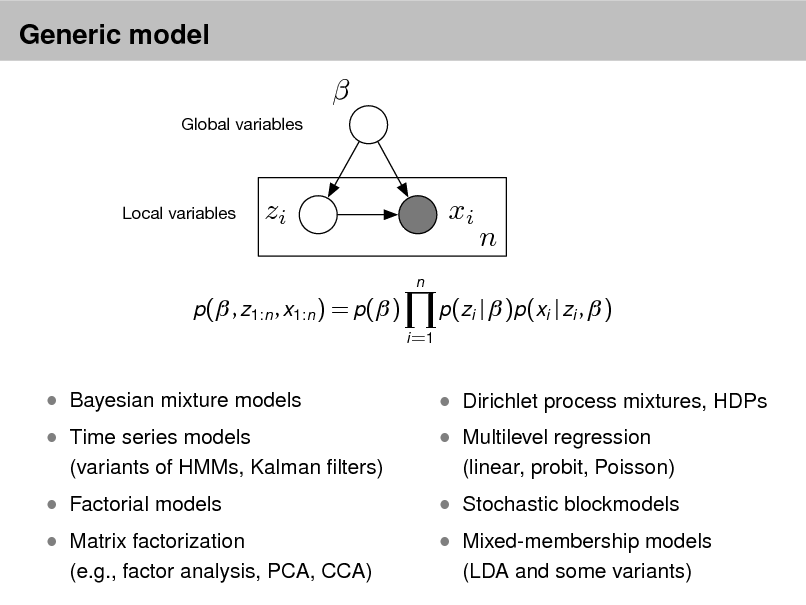
Generic model
Global variables
Local variables
zi
n
xi
n
p( , z1:n , x1:n ) = p( )
i =1
p(zi | )p(xi | zi , )
Bayesian mixture models Time series models Factorial models
(variants of HMMs, Kalman lters)
Dirichlet process mixtures, HDPs Multilevel regression
(linear, probit, Poisson)
Matrix factorization
Stochastic blockmodels
(e.g., factor analysis, PCA, CCA)
Mixed-membership models
(LDA and some variants)
154
![Slide: Mean-eld variational inference
ELBO
xi i n
zi n
zi
Introduce a variational distribution over the latent variables q ( , z ). We optimize the evidence lower bound (ELBO) with respect to q,
log p(x ) Eq [log p( , Z , x )] Eq [log q ( , Z )].
Up to a constant, this is the negative KL between q and the posterior.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_155.png)
Mean-eld variational inference
ELBO
xi i n
zi n
zi
Introduce a variational distribution over the latent variables q ( , z ). We optimize the evidence lower bound (ELBO) with respect to q,
log p(x ) Eq [log p( , Z , x )] Eq [log q ( , Z )].
Up to a constant, this is the negative KL between q and the posterior.
155
![Slide: Mean-eld variational inference
ELBO
xi i n
zi n
zi
We can derive the ELBO with Jensens inequality: log p(x )
= log = log
p( , Z , X )dZd p( , Z , X ) q ( , Z ) q ( , Z ) q (Z ) dZd dZd
q ( , Z ) log
p( , Z , X )
= Eq [log p( , Z , x )] Eq [log q ( , Z )].](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_156.png)
Mean-eld variational inference
ELBO
xi i n
zi n
zi
We can derive the ELBO with Jensens inequality: log p(x )
= log = log
p( , Z , X )dZd p( , Z , X ) q ( , Z ) q ( , Z ) q (Z ) dZd dZd
q ( , Z ) log
p( , Z , X )
= Eq [log p( , Z , x )] Eq [log q ( , Z )].
156
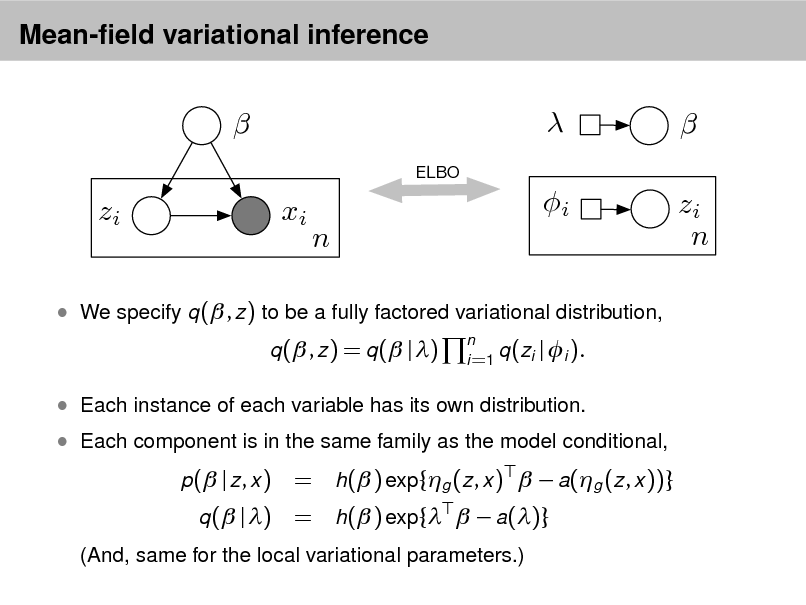
Mean-eld variational inference
ELBO
xi i n
zi n
zi
We specify q ( , z ) to be a fully factored variational distribution,
q ( , z ) = q ( | )
n q (zi i =1
| i ).
Each instance of each variable has its own distribution.
p( | z , x )
Each component is in the same family as the model conditional,
q ( | )
= h( ) exp{g (z , x ) a(g (z , x ))} = h( ) exp{ a()}
(And, same for the local variational parameters.)
157
![Slide: Mean-eld variational inference
ELBO
xi i n
zi n
zi
We optimize the ELBO with respect to these parameters,
(, 1:n ) = Eq [log p( , Z , x )] Eq [log q ( , Z )].
Same as nding the q ( , z ) that is closest in KL divergence to p( , z | x ) The ELBO links the observations/model to the variational distribution.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_158.png)
Mean-eld variational inference
ELBO
xi i n
zi n
zi
We optimize the ELBO with respect to these parameters,
(, 1:n ) = Eq [log p( , Z , x )] Eq [log q ( , Z )].
Same as nding the q ( , z ) that is closest in KL divergence to p( , z | x ) The ELBO links the observations/model to the variational distribution.
158
![Slide: Mean-eld variational inference
ELBO
xi i n
zi n
zi
Coordinate ascent: Iteratively update each parameter, holding others xed. With respect to the global parameter, the gradient is
= a ()(E [g (Z , x )] ).
This leads to a simple coordinate update
= E g (Z , x ) .
The local parameter is analogous.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_159.png)
Mean-eld variational inference
ELBO
xi i n
zi n
zi
Coordinate ascent: Iteratively update each parameter, holding others xed. With respect to the global parameter, the gradient is
= a ()(E [g (Z , x )] ).
This leads to a simple coordinate update
= E g (Z , x ) .
The local parameter is analogous.
159
![Slide: Mean-eld variational inference
Initialize randomly. Repeat until the ELBO converges
1
For each data point, update the local variational parameters:
i
2
(t )
= E(t 1) [ ( , xi )] for i {1, . . . , n}.
(t ) = E (t ) [g (Z1:n , x1:n )].
Update the global variational parameters:](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_160.png)
Mean-eld variational inference
Initialize randomly. Repeat until the ELBO converges
1
For each data point, update the local variational parameters:
i
2
(t )
= E(t 1) [ ( , xi )] for i {1, . . . , n}.
(t ) = E (t ) [g (Z1:n , x1:n )].
Update the global variational parameters:
160
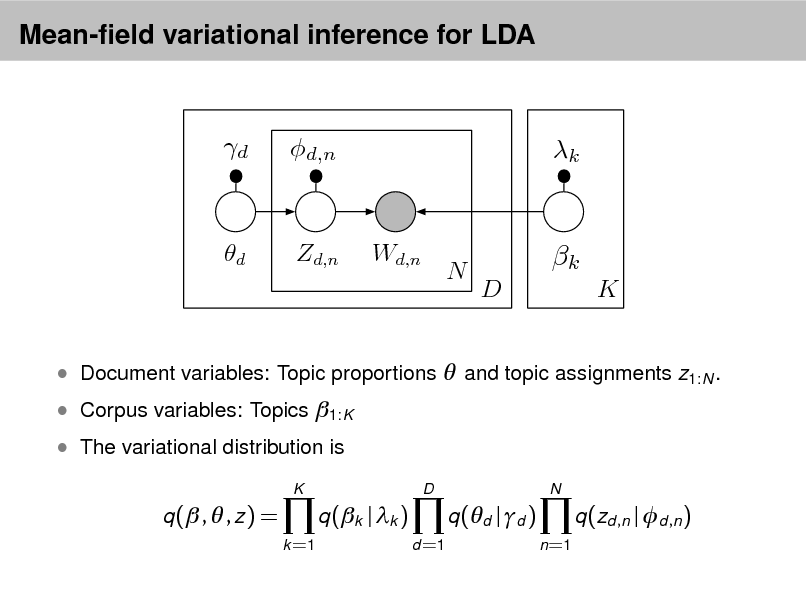
Mean-eld variational inference for LDA
d
d,n
k
d
Zd,n
Wd,n
N
k
D K
Document variables: Topic proportions and topic assignments z1:N . Corpus variables: Topics 1:K The variational distribution is
K
D
N
q ( , , z ) =
k =1
q (k | k )
d =1
q (d | d )
n =1
q (zd ,n | d ,n )
161
![Slide: Mean-eld variational inference for LDA
d
d,n
k
d
Zd,n
Wd,n
N
k
D K
In the local step we iteratively update the parameters for each document,
holding the topic parameters xed.
(t +1) n
(t +1)
= +
exp{
(t ) N n=1 n
q [log ] + q [log .,wn ]}.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_162.png)
Mean-eld variational inference for LDA
d
d,n
k
d
Zd,n
Wd,n
N
k
D K
In the local step we iteratively update the parameters for each document,
holding the topic parameters xed.
(t +1) n
(t +1)
= +
exp{
(t ) N n=1 n
q [log ] + q [log .,wn ]}.
162
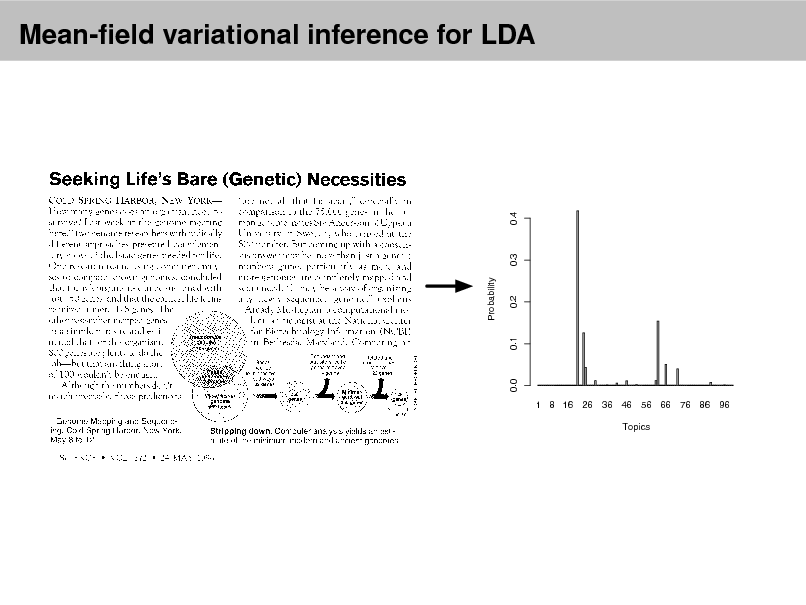
Mean-eld variational inference for LDA
Probability
0.0
1 8 16 26 36 46 56 66 76 86 96 Topics
0.1
0.2
0.3
0.4
163
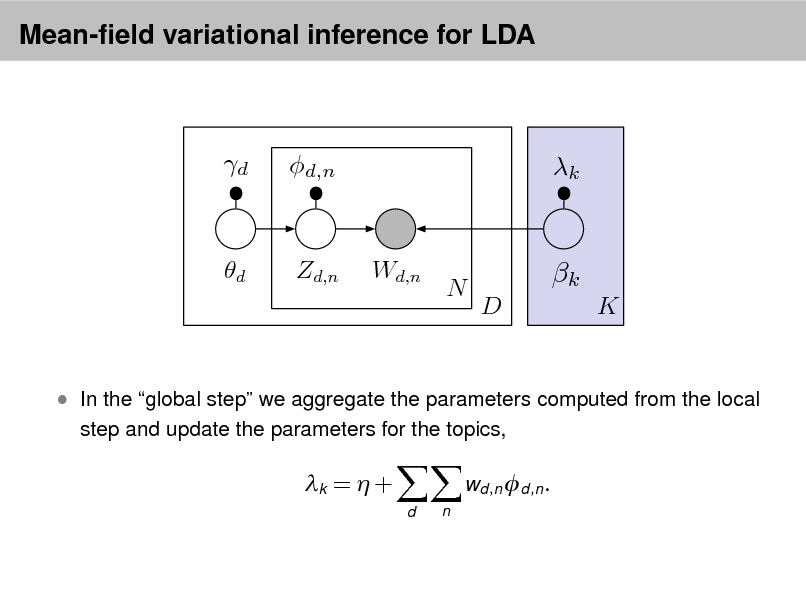
Mean-eld variational inference for LDA
d
d,n
k
d
Zd,n
Wd,n
N
k
D K
In the global step we aggregate the parameters computed from the local
step and update the parameters for the topics,
k = +
d n
wd ,n d ,n .
164

Mean-eld variational inference for LDA
Genetics human genome dna genetic genes sequence gene molecular sequencing map information genetics mapping project sequences Evolution Disease evolution disease evolutionary host species bacteria organisms diseases life resistance origin bacterial biology new groups strains phylogenetic control living infectious diversity malaria group parasite new parasites two united common tuberculosis Computers computer models information data computers system network systems model parallel methods networks software new simulations
165

Mean-eld variational inference for LDA
1: 2: 3: 4: 5: 6: 7: 8: 9: 10:
Initialize topics randomly. repeat for each document do repeat Update the topic assignment variational parameters. Update the topic proportions variational parameters. until document objective converges end for Update the topics from aggregated per-document parameters. until corpus objective converges.
166
![Slide: Mean-eld variational inference
Initialize randomly. Repeat until the ELBO converges
1
Update the local variational parameters for each data point,
i
2
(t )
= E(t 1) [ ( , xi )] for i {1, . . . , n}.
(t ) = E (t ) [g (Z1:n , x1:n )].
Update the global variational parameters,
But we must analyze the whole data set before completing one iteration.
Note the relationship to existing algorithms like EM and Gibbs sampling.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_167.png)
Mean-eld variational inference
Initialize randomly. Repeat until the ELBO converges
1
Update the local variational parameters for each data point,
i
2
(t )
= E(t 1) [ ( , xi )] for i {1, . . . , n}.
(t ) = E (t ) [g (Z1:n , x1:n )].
Update the global variational parameters,
But we must analyze the whole data set before completing one iteration.
Note the relationship to existing algorithms like EM and Gibbs sampling.
167
![Slide: Mean-eld variational inference
Initialize randomly. Repeat until the ELBO converges
1
Update the local variational parameters for each data point,
i
2
(t )
= E(t 1) [ ( , xi )] for i {1, . . . , n}.
(t ) = E (t ) [g (Z1:n , x1:n )].
Update the global variational parameters,
To make this more efcient, we need two ideas:
Stochastic optimization
Natural gradients](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_168.png)
Mean-eld variational inference
Initialize randomly. Repeat until the ELBO converges
1
Update the local variational parameters for each data point,
i
2
(t )
= E(t 1) [ ( , xi )] for i {1, . . . , n}.
(t ) = E (t ) [g (Z1:n , x1:n )].
Update the global variational parameters,
To make this more efcient, we need two ideas:
Stochastic optimization
Natural gradients
168
![Slide: The natural gradient
R IEMANNIAN C ONJUGATE G RADIENT FOR VB
! " #$%&'()* +'(,%))'%)-#$%&'()*
(from Honkela et al., 2010)
In natural gradient ascent, we premultiply the gradient by the inverse of a
Riemannian metric. Amari (1998) showed this is the steepest direction.
Figure 1: Gradient and Riemannian gradient directions are shown for the mean of distribution q. VB learning with a diagonal covariance is applied to the posterior p(x, y) ! exp[9(xy 1)2 x2 y2 ]. The Riemannian gradient strengthens the updates in the directions where the uncertainty is large.
For distributions, the Riemannian metric is the Fisher information.
the conjugate gradient algorithm with their Riemannian counterparts: Riemannian inner products and norms, parallel transport of gradient vectors between different tangent spaces as well as line searches and steps along geodesics in the Riemannian space. In practical algorithms some of these](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_169.png)
The natural gradient
R IEMANNIAN C ONJUGATE G RADIENT FOR VB
! " #$%&'()* +'(,%))'%)-#$%&'()*
(from Honkela et al., 2010)
In natural gradient ascent, we premultiply the gradient by the inverse of a
Riemannian metric. Amari (1998) showed this is the steepest direction.
Figure 1: Gradient and Riemannian gradient directions are shown for the mean of distribution q. VB learning with a diagonal covariance is applied to the posterior p(x, y) ! exp[9(xy 1)2 x2 y2 ]. The Riemannian gradient strengthens the updates in the directions where the uncertainty is large.
For distributions, the Riemannian metric is the Fisher information.
the conjugate gradient algorithm with their Riemannian counterparts: Riemannian inner products and norms, parallel transport of gradient vectors between different tangent spaces as well as line searches and steps along geodesics in the Riemannian space. In practical algorithms some of these
169
![Slide: The natural gradient
ELBO
xi i n
zi n
zi
In the exponential family, the Fisher information is the second derivative of
the log normalizer, G = a ().
So, the natural gradient of the ELBO is
= E [g (Z , x )] .
We can compute the natural gradient by computing the coordinate updates
in parallel and subtracting the current variational parameters.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_170.png)
The natural gradient
ELBO
xi i n
zi n
zi
In the exponential family, the Fisher information is the second derivative of
the log normalizer, G = a ().
So, the natural gradient of the ELBO is
= E [g (Z , x )] .
We can compute the natural gradient by computing the coordinate updates
in parallel and subtracting the current variational parameters.
170

Stochastic optimization
Why waste time with the real gradient, when a cheaper noisy estimate of
the gradient will do (Robbins and Monro, 1951)?
Idea: Follow a noisy estimate of the gradient with a step-size. By decreasing the step-size according to a certain schedule, we guarantee
convergence to a local optimum.
171
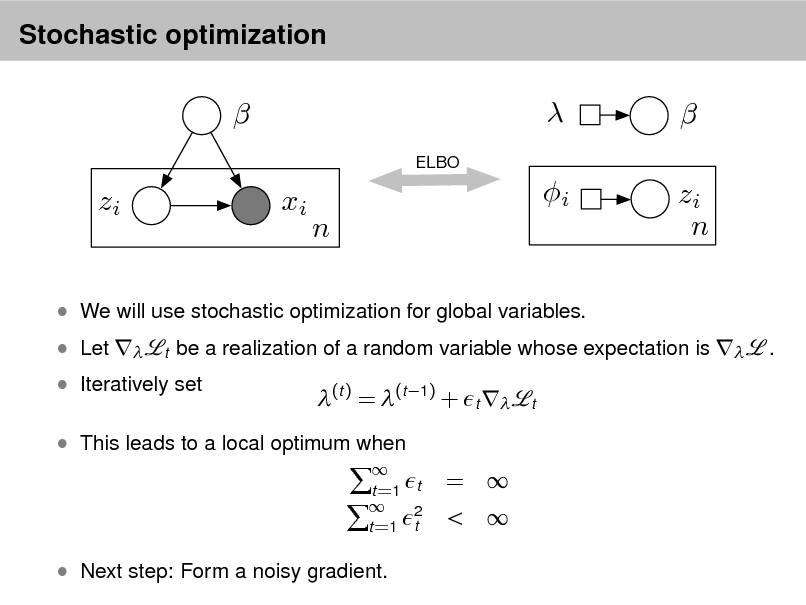
Stochastic optimization
ELBO
xi i n
zi n
zi
Iteratively set
Let
We will use stochastic optimization for global variables.
t
be a realization of a random variable whose expectation is
.
(t ) = (t 1) + t
t
This leads to a local optimum when
t =1
t
=
<
2 t =1 t
Next step: Form a noisy gradient.
172
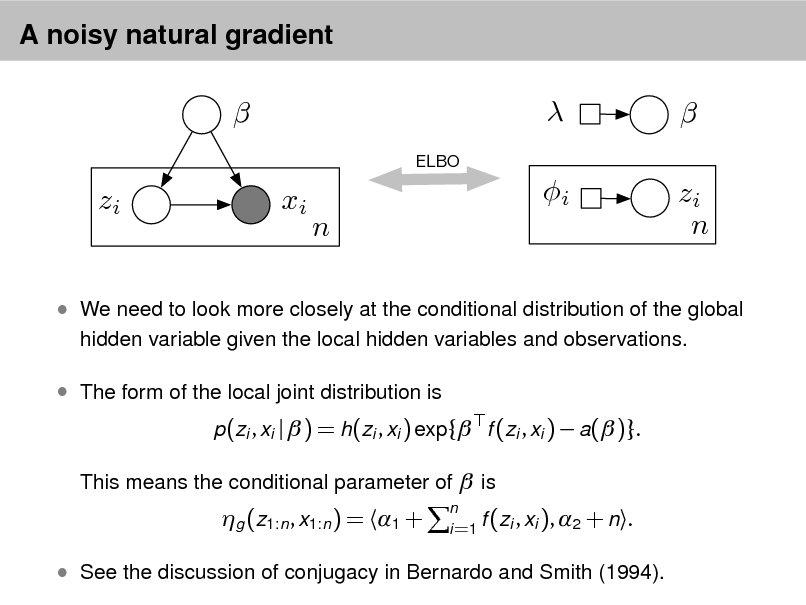
A noisy natural gradient
ELBO
xi i n
zi n
zi
We need to look more closely at the conditional distribution of the global
hidden variable given the local hidden variables and observations.
The form of the local joint distribution is
p(zi , xi | ) = h(zi , xi ) exp{ f (zi , xi ) a( )}.
This means the conditional parameter of is
g (z1:n , x1:n ) = 1 +
n f (zi , xi ), 2 + n. i =1
See the discussion of conjugacy in Bernardo and Smith (1994).
173
![Slide: A noisy natural gradient
With local and global variables, we decompose the ELBO
= E[log p( )] E[log q ( )] +
n E[log p(zi , xi i =1
| )] E[log q (zi )]
Sample a single data point t uniformly from the data and dene
t
= E[log p( )] E[log q ( )] + n(E[log p(zt , xt | )] E[log q (zt )]).
1. The ELBO is the expectation of t with respect to the sample. 2. The gradient of the t-ELBO is a noisy gradient of the ELBO. 3. The t-ELBO is like an ELBO where we saw xt repeatedly.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_174.png)
A noisy natural gradient
With local and global variables, we decompose the ELBO
= E[log p( )] E[log q ( )] +
n E[log p(zi , xi i =1
| )] E[log q (zi )]
Sample a single data point t uniformly from the data and dene
t
= E[log p( )] E[log q ( )] + n(E[log p(zt , xt | )] E[log q (zt )]).
1. The ELBO is the expectation of t with respect to the sample. 2. The gradient of the t-ELBO is a noisy gradient of the ELBO. 3. The t-ELBO is like an ELBO where we saw xt repeatedly.
174
![Slide: A noisy natural gradient
Dene the conditional as though our whole data set is n replications of xt ,
t (zt , xt ) = 1 + n f (zt , xt ), 2 + n
The noisy natural gradient of the ELBO is
= Et [t (Zt , xt )] . t
This only requires the local variational parameters of one data point. In contrast, the full natural gradient requires all local parameters.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_175.png)
A noisy natural gradient
Dene the conditional as though our whole data set is n replications of xt ,
t (zt , xt ) = 1 + n f (zt , xt ), 2 + n
The noisy natural gradient of the ELBO is
= Et [t (Zt , xt )] . t
This only requires the local variational parameters of one data point. In contrast, the full natural gradient requires all local parameters.
175
![Slide: Stochastic variational inference
Initialize global parameters randomly. Set the step-size schedule t appropriately. Repeat forever
1
Sample a data point uniformly, xt Uniform(x1 , . . . , xn ).
2
Compute its local variational parameter,
= E(t 1) [ ( , xt )].
3
Pretend its the only data point in the data set,
= E [t (Zt , xt )].
4
Update the current global variational parameter,
(t ) = (1 t )(t 1) + t .](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_176.png)
Stochastic variational inference
Initialize global parameters randomly. Set the step-size schedule t appropriately. Repeat forever
1
Sample a data point uniformly, xt Uniform(x1 , . . . , xn ).
2
Compute its local variational parameter,
= E(t 1) [ ( , xt )].
3
Pretend its the only data point in the data set,
= E [t (Zt , xt )].
4
Update the current global variational parameter,
(t ) = (1 t )(t 1) + t .
176
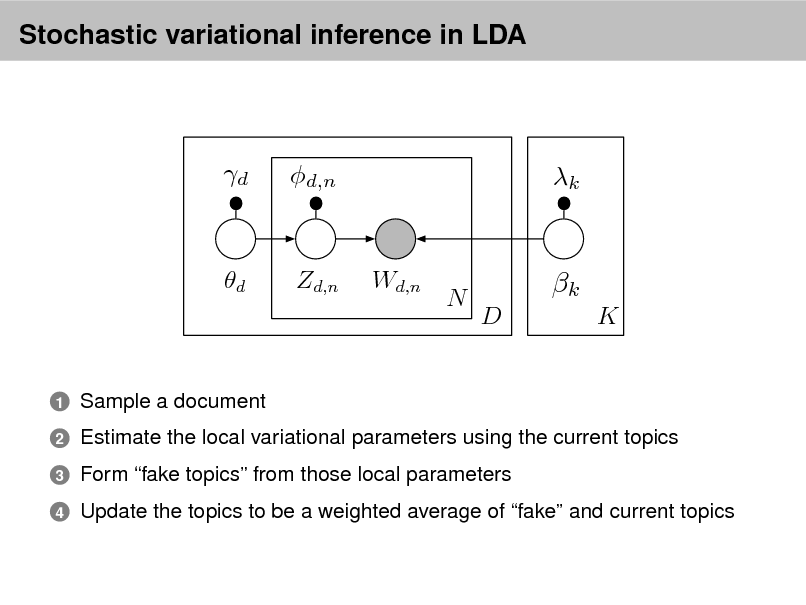
Stochastic variational inference in LDA
d
d,n
k
d
Zd,n
Wd,n
N
k
D K
1 2 3 4
Sample a document Estimate the local variational parameters using the current topics Form fake topics from those local parameters Update the topics to be a weighted average of fake and current topics
177
![Slide: Stochastic variational inference in LDA
1: 2: 3: 4: 5: 6: 7: 8: 9: 10:
Compute k = + D n wt ,n t ,n 11: Set k = (1 t )k + t k . 12: end for
Dene t (0 + t ) Initialize randomly. for t = 0 to do Choose a random document wt Initialize tk = 1. (The constant 1 is arbitrary.) repeat Set t ,n exp{ q [log t ] + q [log ,wn ]} Set t = + n t ,n 1 until K k |change in t ,k | <](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_178.png)
Stochastic variational inference in LDA
1: 2: 3: 4: 5: 6: 7: 8: 9: 10:
Compute k = + D n wt ,n t ,n 11: Set k = (1 t )k + t k . 12: end for
Dene t (0 + t ) Initialize randomly. for t = 0 to do Choose a random document wt Initialize tk = 1. (The constant 1 is arbitrary.) repeat Set t ,n exp{ q [log t ] + q [log ,wn ]} Set t = + n t ,n 1 until K k |change in t ,k | <
178
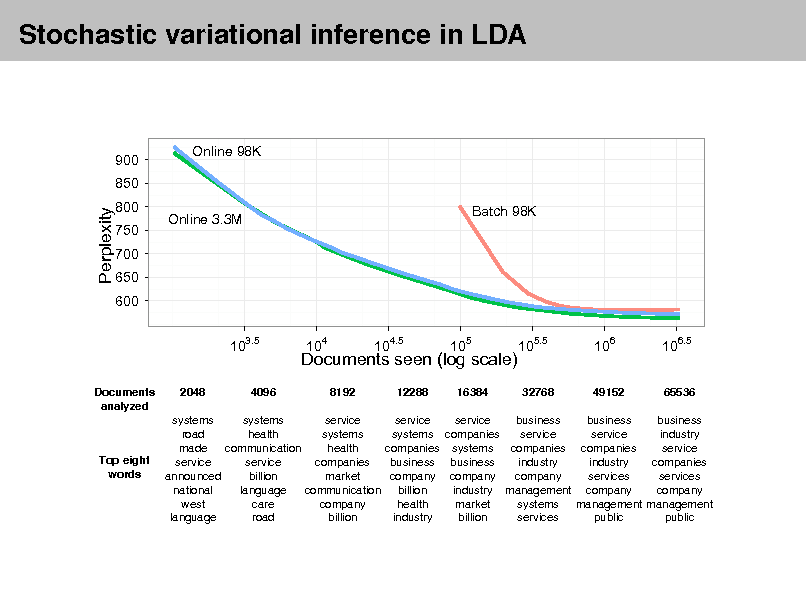
Stochastic variational inference in LDA
900 850 800 750 700 650 600
Online 98K
Perplexity
Online 3.3M
Batch 98K
103.5
Documents analyzed 2048 4096
Documents seen (log scale)
8192 12288 16384
104
104.5
105
105.5
32768
106
49152
106.5
65536
Top eight words
systems systems service road health systems made communication health service service companies announced billion market national language communication west care company language road billion
service service business business business systems companies service service industry companies systems companies companies service business business industry industry companies company company company services services billion industry management company company health market systems management management industry billion services public public
179
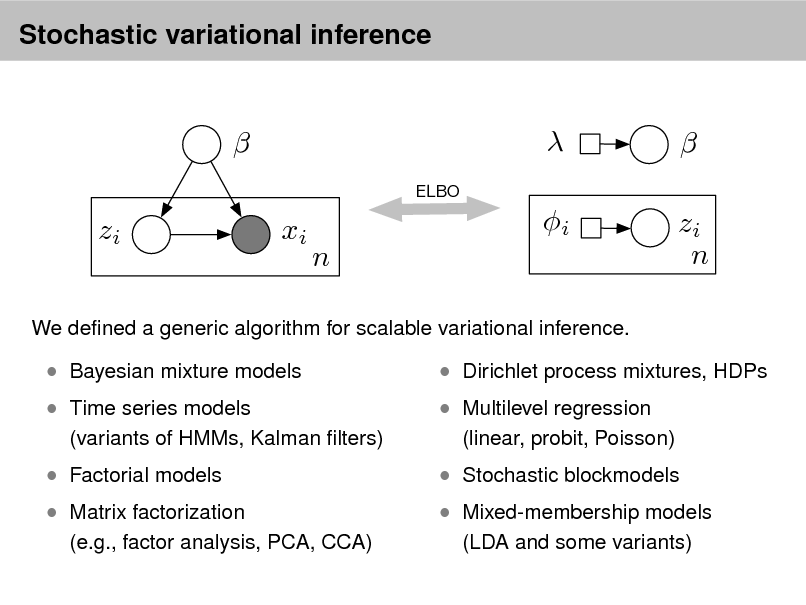
Stochastic variational inference
ELBO
xi i n
zi n
zi
We dened a generic algorithm for scalable variational inference.
Bayesian mixture models Time series models Factorial models
(variants of HMMs, Kalman lters)
Dirichlet process mixtures, HDPs Multilevel regression
(linear, probit, Poisson)
Matrix factorization
Stochastic blockmodels
(e.g., factor analysis, PCA, CCA)
Mixed-membership models
(LDA and some variants)
180
Stochastic variational inference
ELBO
xi i n
zi n
zi
See Wang et al. (2010) for Bayesian nonparametric models (and code). See Sato (2001) for the original stochastic variational inference. See Honkela et al. (2010) for natural gradients and variational inference.
See Hoffman et al. (2010) for LDA (and code).
181
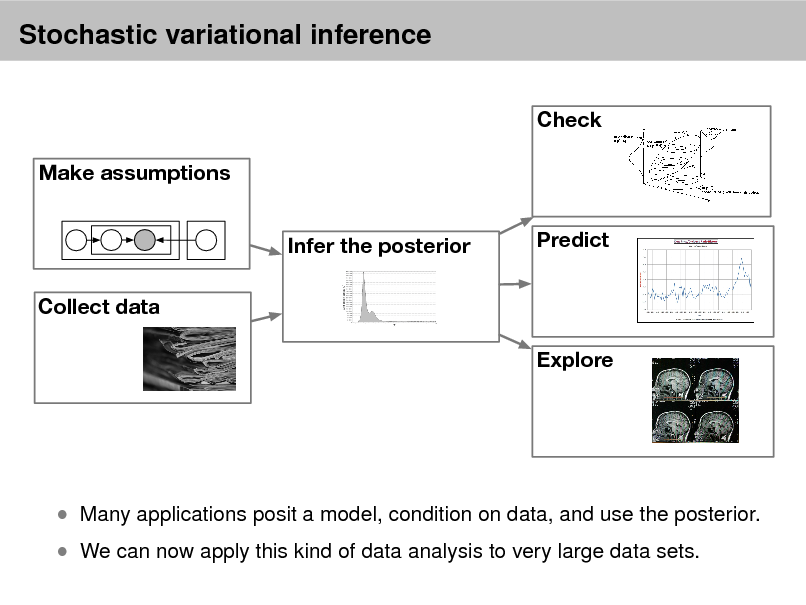
Stochastic variational inference
Check Make assumptions Infer the posterior Collect data Explore Predict
We can now apply this kind of data analysis to very large data sets.
Many applications posit a model, condition on data, and use the posterior.
182

Nonconjugate variational inference
The class of conditionally conjugate models is very exible. However, some modelslike the CTM and DTMdo not t in. In the past, researchers developed tailored optimization procedures for
tting the variational objective.
We recently developed a more general approach that subsumes many of
these strategies.
183
![Slide: Nonconjugate variational inference
Bishop (2006) showed that the optimal mean-eld variational distribution is
q (z ) q ( )
exp Eq ( ) [log p(z | , x )] exp Eq (z ) [log p( | z , x )]
In conjugate models, we can compute these expectations.
This determines the form of the optimal variational distribution.
In nonconjugate models we cant compute the expectations. But, under certain conditions, we can use Taylor approximations.
This leads to Gaussian variational distributions.](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_184.png)
Nonconjugate variational inference
Bishop (2006) showed that the optimal mean-eld variational distribution is
q (z ) q ( )
exp Eq ( ) [log p(z | , x )] exp Eq (z ) [log p( | z , x )]
In conjugate models, we can compute these expectations.
This determines the form of the optimal variational distribution.
In nonconjugate models we cant compute the expectations. But, under certain conditions, we can use Taylor approximations.
This leads to Gaussian variational distributions.
184

Using and Checking Topic Models
185
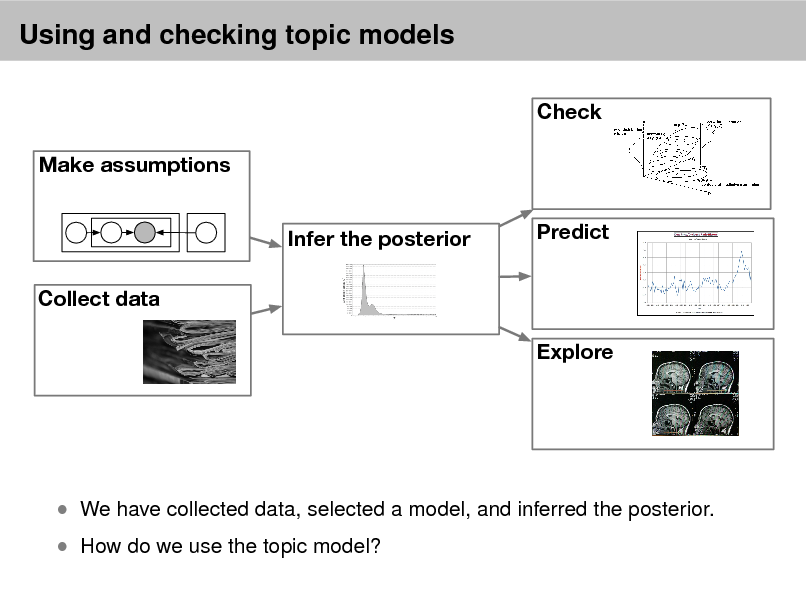
Using and checking topic models
Check Make assumptions Infer the posterior Collect data Explore Predict
How do we use the topic model?
We have collected data, selected a model, and inferred the posterior.
186
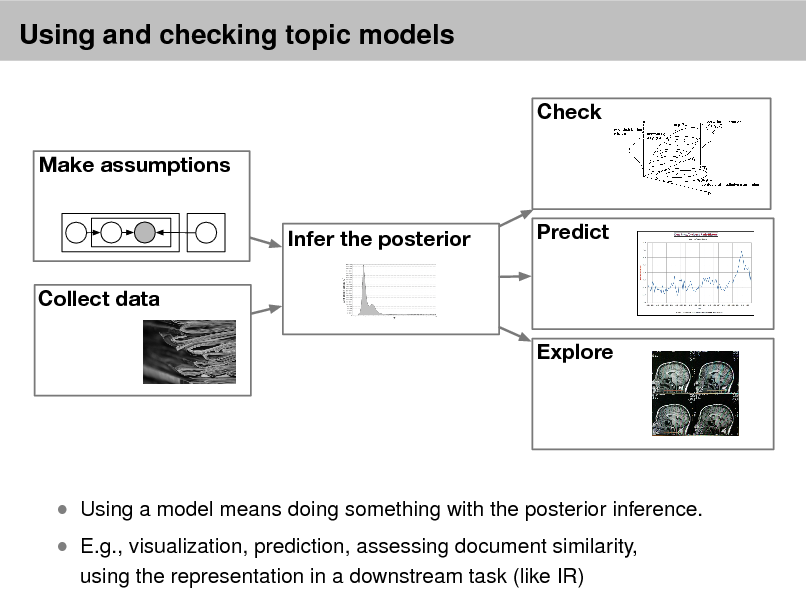
Using and checking topic models
Check Make assumptions Infer the posterior Collect data Explore Predict
E.g., visualization, prediction, assessing document similarity,
using the representation in a downstream task (like IR)
Using a model means doing something with the posterior inference.
187
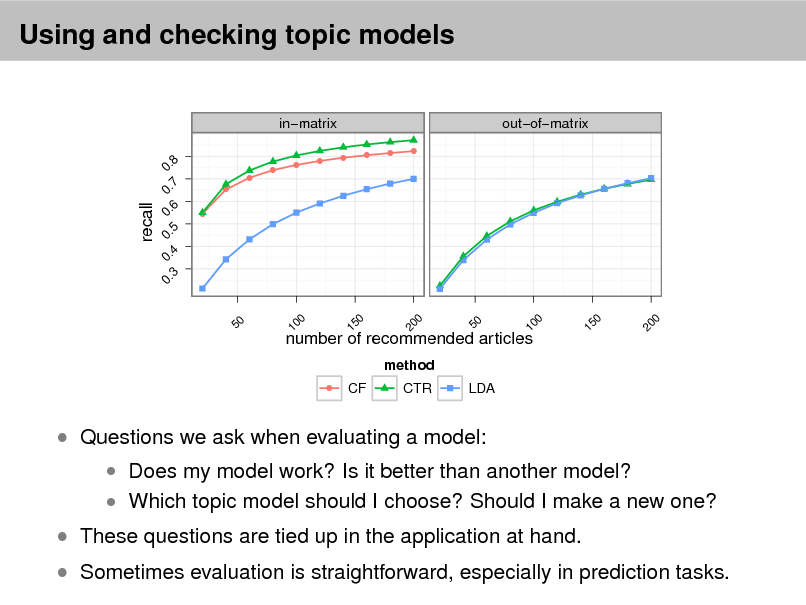
Using and checking topic models
inmatrix
0. 8
q q q q q q
outofmatrix
q
q
7
recall
0.
6
0.
q q
0.
3
0.
4
0.
5
10 0
15 0
20 0
10 0
15 0
number of recommended articles
method
q
CF
CTR
LDA
Questions we ask when evaluating a model:
These questions are tied up in the application at hand.
Does my model work? Is it better than another model? Which topic model should I choose? Should I make a new one?
Sometimes evaluation is straightforward, especially in prediction tasks.
20 0
50
50
188

Using and checking topic models
But a promise of topic models is that they give good exploratory tools. And this leads to more questions:
Evaluation is complicated, e.g., is this a good navigator of my collection?
How do I interpret a topic model? What quantities help me understand what it says about the data?
189

Using and checking topic models
How to interpret and evaluate topic models is an active area of research.
Visualizing topic models Naming topics
Matching topic models to human judgements Matching topic models to external ontologies
Computing held out likelihoods in different ways
I will discuss two components:
Predictive scores for evaluating topic models Posterior predictive checks for topic modeling
190
![Slide: The predictive score
Assess how well a model can predict future data In text, a natural setting is one where we observe part of a new document
and want to predict the remainder.
The predictive distribution is a distribution conditioned on the corpus and
the partial document, p (w |
, wobs ) =
K k =1 k k ,w
p( | wobs , )p( | q ( )q ( )
)
K k =1 k k , w
= Eq [ | wobs ] Eq [,w | ].](https://yosinski.com/mlss12/media/slides/MLSS-2012-Blei-Probabilistic-Topic-Models_191.png)
The predictive score
Assess how well a model can predict future data In text, a natural setting is one where we observe part of a new document
and want to predict the remainder.
The predictive distribution is a distribution conditioned on the corpus and
the partial document, p (w |
, wobs ) =
K k =1 k k ,w
p( | wobs , )p( | q ( )q ( )
)
K k =1 k k , w
= Eq [ | wobs ] Eq [,w | ].
191

The predictive score
The predictive score evaluates the remainder of the document
independently under this distribution. s=
w wheld out
log p(w |
, wobs )
(1)
In the predictive distribution, q is any approximate poterior. This puts
various models and inference procedures on the same scale.
(In contrast, perplexity of entire held out documents requires different
approximations for each inference method.)
192
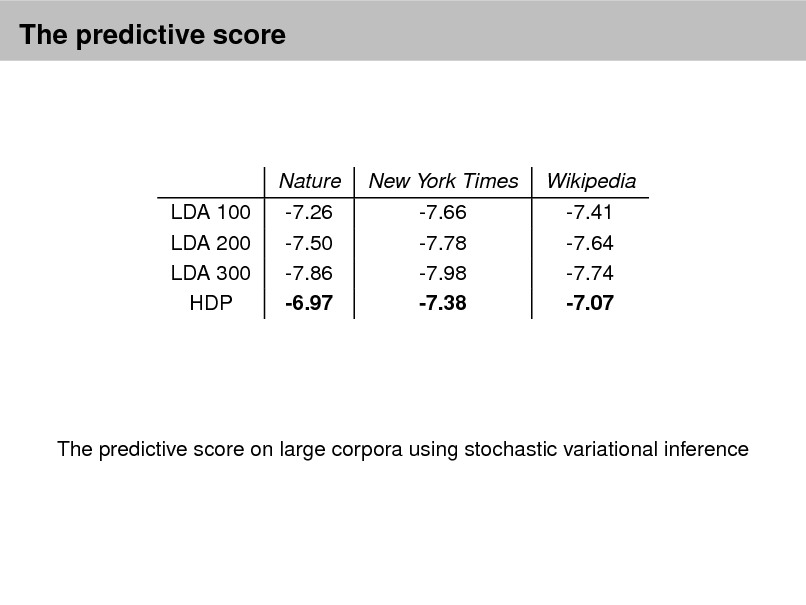
The predictive score
LDA 100 LDA 200 LDA 300 HDP
Nature -7.26 -7.50 -7.86 -6.97
New York Times -7.66 -7.78 -7.98 -7.38
Wikipedia -7.41 -7.64 -7.74 -7.07
The predictive score on large corpora using stochastic variational inference
193

Posterior predictive checks
The predictive score and other model selection criteria are good for
choosing among several models.
But they dont help with the model building process; they dont tell us how a
model is mist. (E.g. should I go from LDA to a DTM or LDA to a CTM?)
Further, prediction is not always important in exploratory or descriptive
tasks. We may want models that capture other aspects of the data.
Posterior predictive checks are a technique from Bayesian statistics that
help with these issues.
194
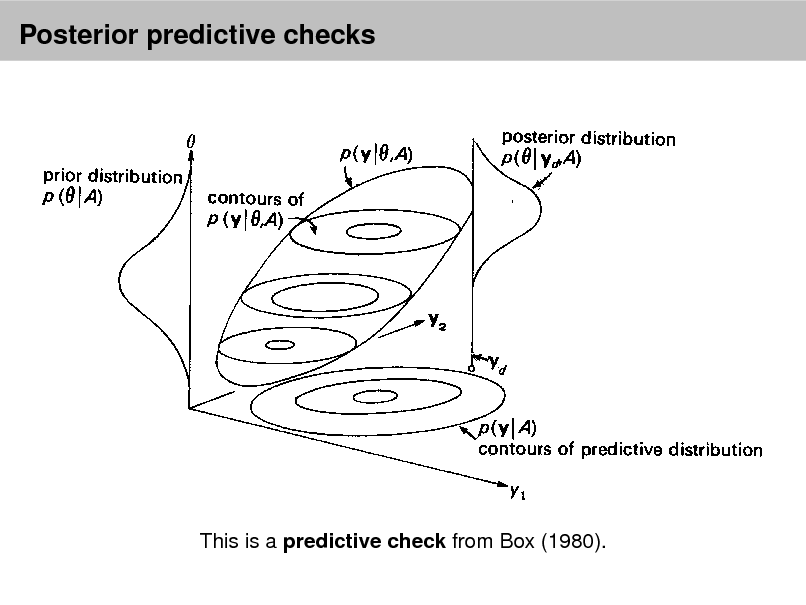
Posterior predictive checks
he intuitions about how to assess a model are in this picture:
This is a predictive check from Box (1980).
et up from Box (1980) is the following.
195

Posterior predictive checks
Three stages to model building: estimation, criticism, and revision. In criticism, the model confronts our data. Suppose we observe a data set y. The predictive distribution is the
distribution of data if the model is true: p (y | M ) =
p(y | )p( )
Locating y in the predictive distribution indicates if we can trust the model. Or, locating a discrepancy function g (y) in its predictive distribution
indicates if what is important to us is captured in the model.
196

Posterior predictive checks
Rubin (1984) located the data y in the posterior p(y | y, M ). Gelman, Meng, Stern (1996) expanded this idea to realized discrepancies that include hidden variables g (y, z). We might make modeling decisions based on a variety of simplifying
considerations (e.g., algorithmic). But we can design the realized discrepancy function to capture what we really care about.
Further, realized discrepancies let us consider which parts of the model t
well and which parts dont. This is apt in exploratory tasks.
197

Posterior predictive checks in topic models
Consider a decomposition of a corpus into topics, i.e., {wd ,n , zd ,n }. Note
that zd ,n is a latent variable.
For all the observations assigned to a topic, consider the variable {wd ,n , d }.
This is the observed word and the document it appeared in.
One measure of how well a topic model ts the LDA assumptions is to look
at the per-topic mutual information between w and d.
If the words from the topic are independently generated then we expect
lower mutual information.
What is low? To answer that, we can shufe the words and recompute.
This gives values of the MI when the words are independent.
198

most frequent words. Each Posterior tax. words position along the x-axis denotes its specicity to the documents. For example estate in the rst topic predictive checks in topic models is more specic than
Figure 3. A topic model t to the Yale Law Journal. Here, there are 20 topics (the top eight are plotted). Each topic is illustrated with its top-
4
10
3
13
tax
taxation taxes
revenue
income
estate subsidies organizations year consumption earnings 6
trial
exemption
employer employers employment work
workers employees union
labor
women
men sex
sexual
treasury taxpayers funds
employee job bargaining
unions worker
collective industrial
child family children gender woman marriage discrimination male
social female parents
parties contracts party creditors
agreement breach contractual terms bargaining contracting debt exchange limited
16
contract liability
15
1
jury
speech
judges punishment judge crimes evidence sentence jurors
offense guilty
crime defendant defendants sentencing
freedom expression protected culture context equality values conduct
ideas protect content
free amendment
firm value market cost capital shareholders
firms price corporate
constitutional
constitution government justice amendment
history people legislative opinion fourteenth article majority citizens republican
political
stock
information
insurance efficient assets offer share
observed variables. This conditional With this notation, the generative Can use it the posterior model LDA corresponds to the foldistribution is also calledto measureprocess for tness per topic. distribution. lowing joint distribution of the hidden Helps us explore parts of the model that t well. LDA falls precisely into this frame- and observed variables,
This realized discrepancy measures model tness
language for describing families of probability distributions.e The graphical model for LDA is in Figure 4. These three representations are equivalent
199

Discussion
200

Probabilistic topic models
What are topic models?
What kinds of things can they do?
How do I compute with a topic model?
How do I evaluate and check a topic model? How can I learn more?
What are some unanswered questions in this eld?
201
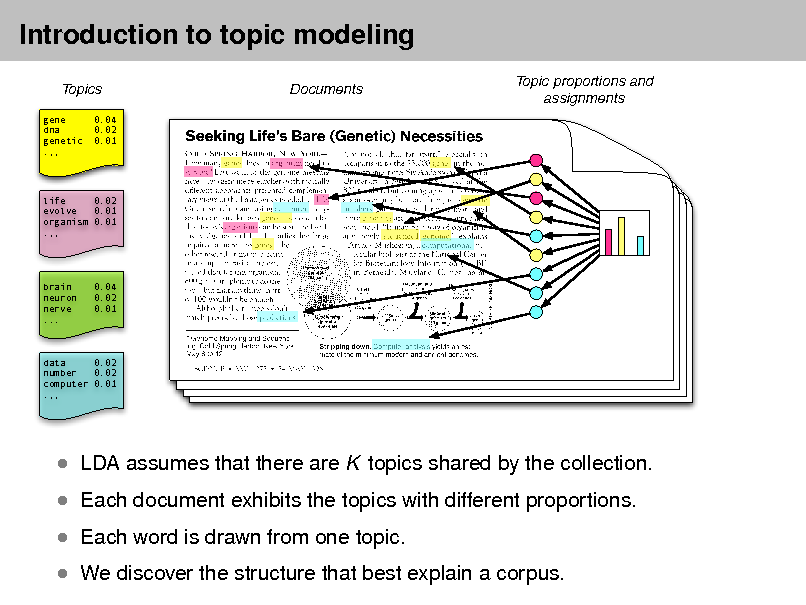
Introduction to topic modeling
Topics
gene dna genetic .,, 0.04 0.02 0.01
Documents
Topic proportions and assignments
life 0.02 evolve 0.01 organism 0.01 .,,
brain neuron nerve ...
0.04 0.02 0.01
data 0.02 number 0.02 computer 0.01 .,,
Each document exhibits the topics with different proportions. Each word is drawn from one topic. We discover the structure that best explain a corpus.
LDA assumes that there are K topics shared by the collection.
202
Extensions of LDA
d Zd,n Wd,n d Zd,n Wd,n d Zd,n Wd,n
i
Zi,n Wi,n
d
2 d
2 u
Yi,j
d
k
Id
Zdn Wdn
Vud
N D
Xu U
Id
Id
j
Zj,n
Wj,n
...
K
k
k,2
k,1
k,2
K
d
Zdn Wdn
2 d
2 u
,
d
Zd,n
Wd,n
N
D
k
K
d
Zdn
2 d
2 u
Ad , Bd
N
Vud
D
Xu U
d
Zd,n
Wd,n
N
k K
Wdn
Ad , Bd
N
Vud
D
Xu U
k
k
K
Yd
D
,
K
Topic models can be adapted to many settings
combine models
relax assumptions
model more complex data
203
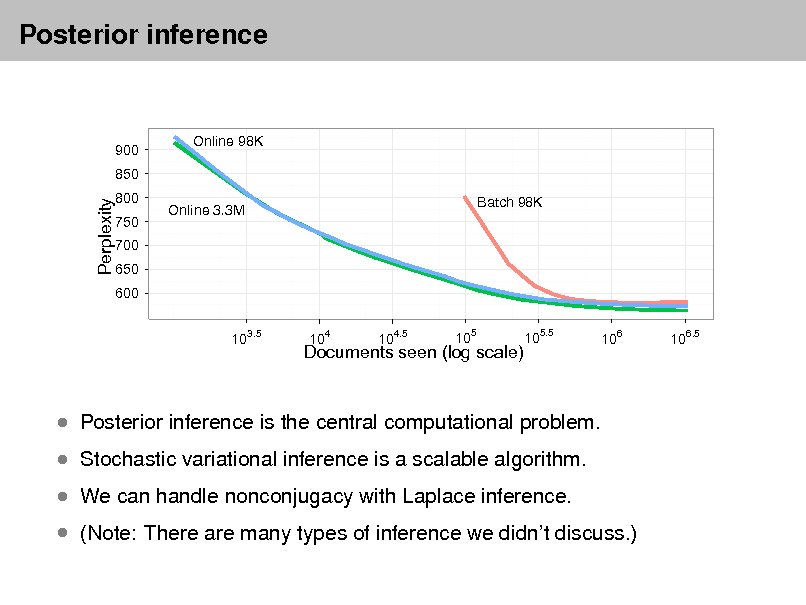
Posterior inference
900 850 800 750 700 650 600
Online 98K
Perplexity
Online 3.3M
Batch 98K
103.5
Documents analyzed 2048 4096
Documents seen (log scale)
8192 12288 16384
104
104.5
105
105.5
32768
106
49152
106.5
65536
Top eight Stochastic variational inference is a scalable algorithm. words
Posterior inference is the central computational problem.
We can handle nonconjugacy with Laplace inference.
systems systems service road health systems made communication health service service companies announced billion market national language communication west care company language road billion
service service business business business systems companies service service industry companies systems companies companies service business business industry industry companies company company company services services billion industry management company company health market systems management management industry billion services public public
(Note: There are many types of inference we didnt discuss.)
204
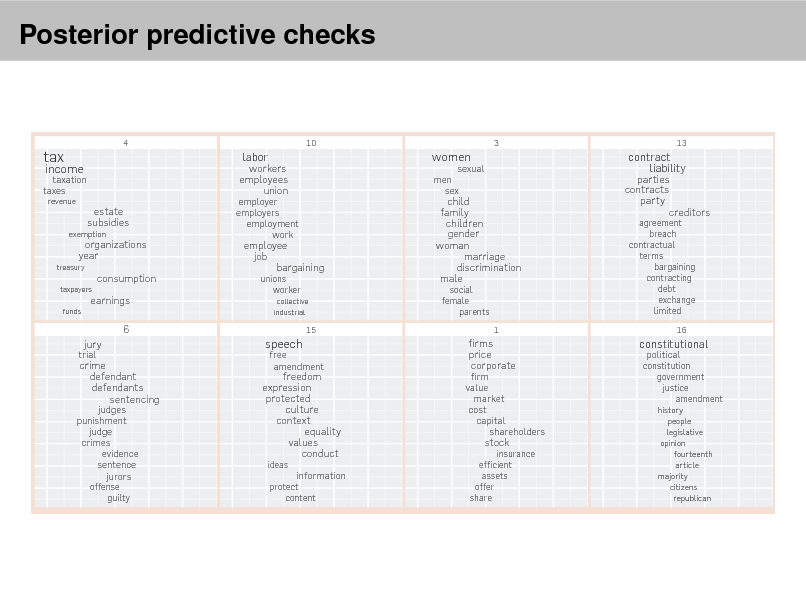
eview articles
Posterior predictive checks
Figure 3. A topic model t to the Yale Law Journal. Here, there are 20 topics (the top eight are plotted). Each topic is illustrated with its topmost frequent words. Each words position along the x-axis denotes its specicity to the documents. For example estate in the rst topic is more specic than tax.
4
10
3
13
tax
taxation taxes
revenue
income
estate subsidies organizations year consumption earnings 6
trial
exemption
employer employers employment work
workers employees union
labor
women
men sex
sexual
treasury taxpayers funds
employee job bargaining
unions worker
collective industrial
child family children gender woman marriage discrimination male
social female parents
parties contracts party creditors
agreement breach contractual terms bargaining contracting debt exchange limited
16
contract liability
15
1
jury
speech
judges punishment judge crimes evidence sentence jurors
offense guilty
crime defendant defendants sentencing
freedom expression protected culture context equality values conduct
ideas protect content
free amendment
firm value market cost capital shareholders
firms price corporate
constitutional
constitution government justice amendment
history people legislative opinion fourteenth article majority citizens republican
political
stock
information
insurance efficient assets offer share
observed variables. This conditional distribution is also called the posterior
With this notation, the generative process for LDA corresponds to the fol-
language for describing families of probability distributions.e The graphi-
205
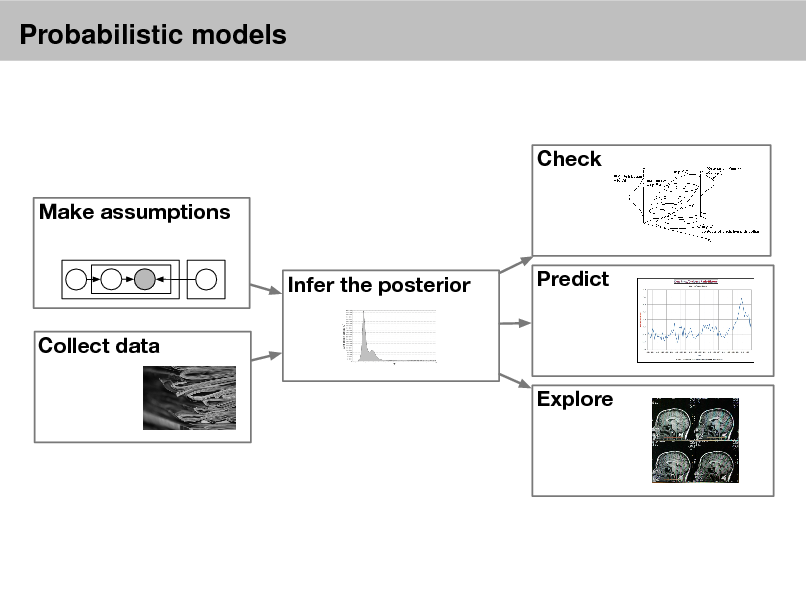
Probabilistic models
Check Make assumptions Infer the posterior Collect data Explore Predict
206

Implementations of LDA
There are many available implementations of topic modeling. Here is an incomplete list LDA-C HDP Online LDA LDA in R LingPipe Mallet TMVE
A C implementation of LDA A C implementation of the HDP (innite LDA) A python package for LDA on massive data Package in R for many topic models Java toolkit for NLP and computational linguistics Java toolkit for statistical NLP A python package to build browsers from topic models
available at www.cs.princeton.edu/blei/
207

Research opportunities in topic modeling
New applications of topic modeling
What methods should we develop to solve problems in the computational social sciences? The digital humanties? Digital medical records?
Interfaces and downstream applications of topic modeling
What can I do with an annotated corpus? How can I incorporate latent variables into a user interface? How should I visualize a topic model?
Model interpretation and model checking
Which model should I choose for which task? What does the model tell me about my corpus?
208

Research opportunities in topic modeling
Incorporating corpus, discourse, or linguistic structure Prediction from text
How can our knowledge of language help inform better topic models?
What is the best way to link topics to prediction?
Theoretical understanding of approximate inference
What do we know about variational inference? Can we analyze it from either the statistical or learning perspective? What are the relative advantages of the many inference methods?
And many specic problems
E.g., sensitivity to the vocabulary, modeling word contagion, modeling complex trends in dynamic models, robust topic modeling, combining graph models with relational models, ...
209

We should seek out unfamiliar summaries of observational material, and establish their useful properties... And still more novelty can come from nding, and evading, still deeper lying constraints.
(J. Tukey, The Future of Data Analysis, 1962)
210

Despite all the computations, you could just dance to the rock n roll station.
(The Velvet Underground, Rock & Roll, 1969)
211
Site based on the django-slidedeck framework by Jason Yosinski.
Find a bug? Email Jason or submit a pull request on Github.