MLSS 2012 in Kyoto

Brain and Reinforcement Learning

Kenji Doya
doya@oist.jp

Neural Computation Unit Okinawa Institute of Science and Technology

Location of Okinawa
Seoul! Beijing!
3 hour! 2.5 hour! 2.5 hour! 2 hour! 1.5 hour!

Tokyo!

Shanghai!

Taipei!
2.5 hour!

Okinawa!

Manila!

Okinawa Institute of Science & Technology
! Apr. 2004: Initial research ! President: Sydney Brenner ! Nov. 2011: Graduate university ! President: Jonathan Dorfan

! Sept. 2012: Ph.D. course ! 20 students/year

Our Research Interests
How to build adaptive, autonomous systems ! robot experiments How the brain realizes robust, flexible adaptation ! neurobiology

Learning to Walk
! Action: cycle of 4 postures ! Reward: speed sensor output

(Doya & Nakano, 1985)

! Problem: a long jump followed by a fall Need for long-term evaluation of action

Reinforcement Learning
reward r ! action a ! state s ! agent! environment!

! Learn action policy: s a to maximize rewards ! Value function: expected future rewards ! V(s(t)) = E[ r(t) + r(t+1) + 2r(t+2) + 3r(t+3) +] V(s(t+1)! 01: discount factor ! Temporal difference (TD) error: ! (t) = r(t) + V(s(t+1)) - V(s(t))

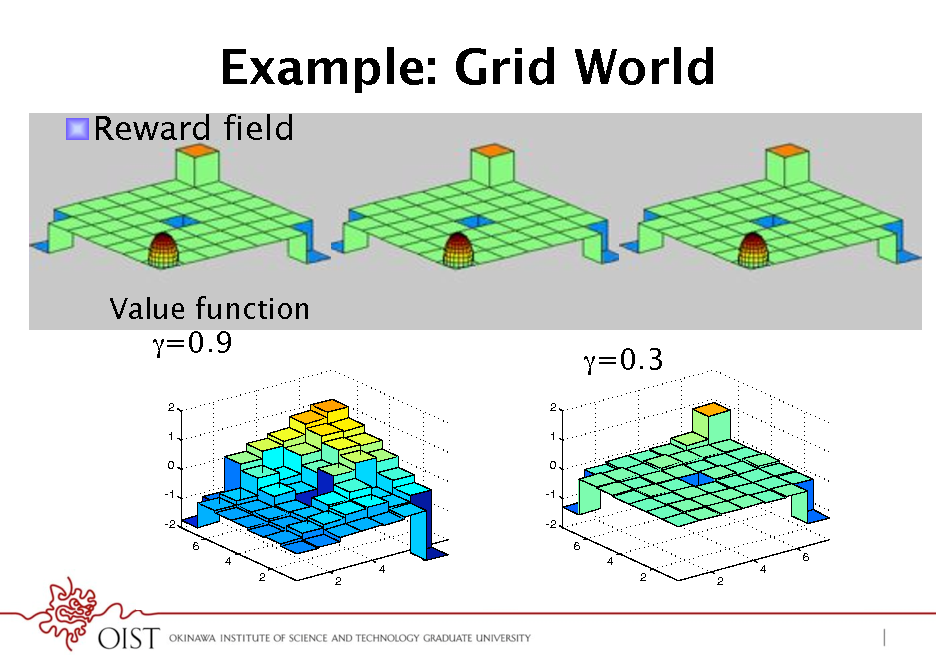
Example: Grid World
! Reward field

Value function
=0.9
2 1 0 -1 -2 6 4 2 2 6 4 2 1 0 -1 -2 6

=0.3

4 2 2

6 4

Cart-Pole Swing-Up
! Reward: height of pole ! Punishment: collision ! Value in 4D state space

Learning to Stand Up

Morimoto & Doya, 2000)

! State: joint/head angles, angular velocity ! Action: torques to motors ! Reward: head height tumble

Learning to Survive and Reproduce
! Catch battery packs
! survival

! Copy genes by IR ports
! reproduction, evolution

Markov Decision Process (MDP)
reward r ! ! Markov decision process ! state s S action a ! ! action a A agent! environment! ! policy p(a|s) state s ! ! reward r(s,a) ! dynamics p(s|s,a) ! Optimal policy: maximize cumulative reward ! finite horizon: E[ r(1) + r(2) + r(3) + ... + r(T)] ! infinite horizon: E[ r(1) + r(2) + 2r(3) + ] 01: temporal discount factor ! average reward: E[ r(1) + r(2) + ... + r(T)]/T, T

Solving MDPs
Dynamic Programming
! ! p(s|s,a) and r(s,a) are known Solve Bellman equation V(s) = maxa E[ r(s,a) + V(s)] ! V(s): value function expected reward from state s Apply optimal policy a = argmaxa E[ r(s,a) + V*(s)] Value iteration Policy iteration

Reinforcement Learning
! ! ! ! ! ! ! ! p(s|s,a) and r(s,a) are unknown Learn from actual experience {s,a,r,s,a,r,} Monte Carlo SARSA Q-learning Actor-Critic Policy gradient Model-based ! learn p(s|s,a), r(s,a) and do DP

! ! !

Actor-Critic and TD learning
! Actor: parameterized policy: P(a|s; w) ! Critic: learn value function V(s(t)) = E[ r(t) + r(t+1) + 2r(t+2) +] ! in a table or a neural network ! Temporal Difference (TD) error: ! (t) = r(t) + V(s(t+1)) - V(s(t)) ! Update ! Critic: V(s(t)) = (t) ! Actor: w = (t) P(a(t)|s(t);w)/w reinforce a(t) by (t)

SARSA and Q Learning
! Action value function ! Q(s,a) = E[ r(t) + r(t+1) + 2r(t+2) | s(t)=s,a(t)=a] ! Action selection ! -greedy: a = argmaxa Q(s,a) with prob 1-* ! Boltzman: P(ai|s) = exp[Q(s,ai)] / jexp[Q(s,aj)] ! SARSA: on-policy update ! Q(s(t),a(t)) = {r(t)+Q(s(t+1),a(t+1))-Q(s(t),a(t))} ! Q learning: off-policy update ! Q(s(t),a(t)) = {r(t)+maxaQ(s(t+1),a)-Q(s(t),a(t))}

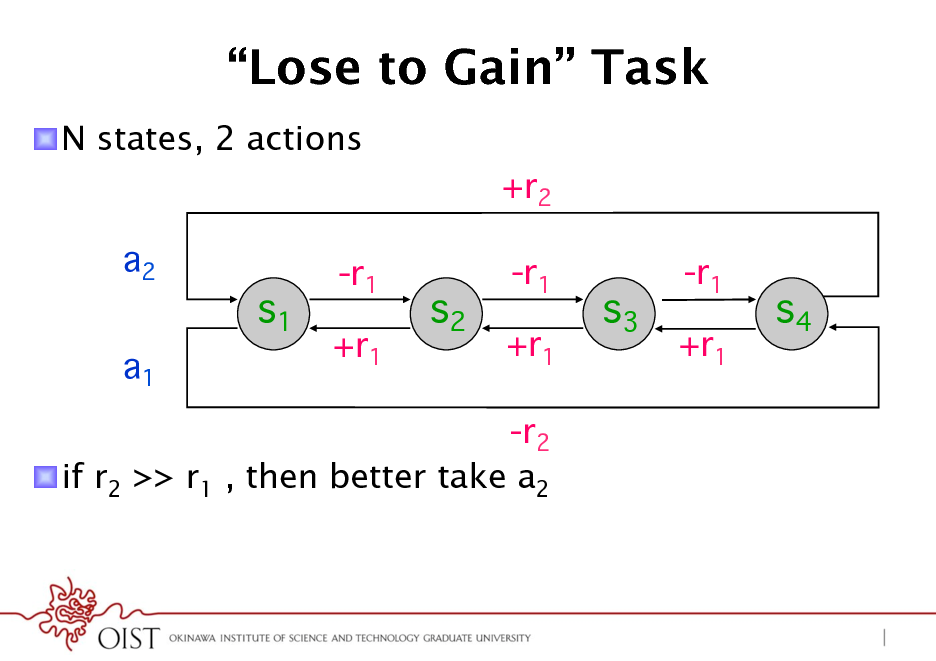
Lose to Gain Task
! N states, 2 actions +r2 a2 a1

s1

-r1 +r1

s2

-r1 +r1

s3

-r1 +r1

s4

-r2 ! if r2 >> r1 , then better take a2

Reinforcement Learning
! Predict reward: value function ! V(s) = E[ r(t) + r(t+1) + 2r(t+2)| s(t)=s] ! Q(s,a) = E[ r(t) + r(t+1) + 2r(t+2)| s(t)=s, a(t)=a] ! Select action How to implement these steps? ! greedy: a = argmax Q(s,a) ! Boltzmann: P(a|s) exp[ Q(s,a)] ! Update prediction: TD error* ! (t) = r(t) + V(s(t+1)) - V(s(t)) How to tune these parameters? ! V(s(t)) = (t) ! Q(s(t),a(t)) = (t)

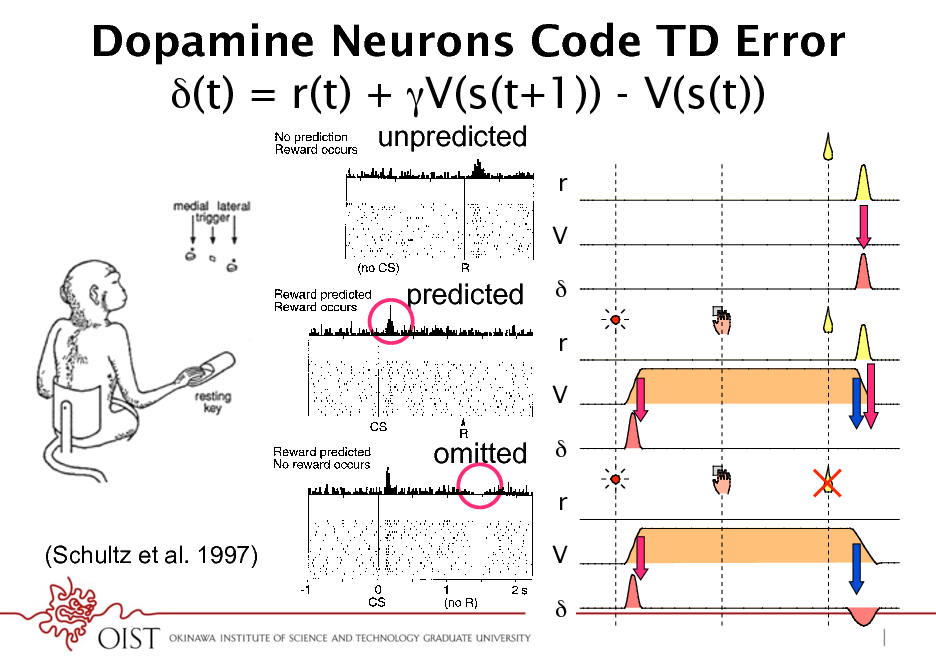
Dopamine Neurons Code TD Error (t) = r(t) + V(s(t+1)) - V(s(t))
4 W. SCHULTZ

unpredicted

rr

V V

predicted

*

rr

V V

fails to occur, even in the absence of an immediately preceding stimulus (Fig. 2, bottom). This is observed when animals fail to obtain reward because of erroneous behavior, when liquid ow is stopped by the experimenter despite correct behavior, or when a valve opens audibly without delivering liquid (Hollerman and Schultz 1996; Ljungberg et al. 1991; Schultz et al. 1993). When reward delivery is delayed for 0.5 or 1.0 s, a depression of neuronal activity occurs at the regular time of the reward, and an activation follows the reward at the new time (Hollerman and Schultz 1996). Both responses occur only during a few repetitions until the new time of reward delivery becomes predicted again. By contrast, delivering reward earlier than habitual results in an activation at the new time of reward but fails to induce a depression at the habitual time. This suggests that unusually early reward delivery cancels the reward prediction for the habitual time. Thus dopamine neurons monitor both the occurrence and the time of reward. In the absence of stimuli immediately preceding the omitted reward, the depressions do not constitute a simple neuronal response but reect an expectation process based on an internal clock tracking the precise time of predicted reward. Activation by conditioned, reward-predicting stimuli About 5570% of dopamine neurons are activated by conditioned visual and auditory stimuli in the various classically or instrumentally conditioned tasks described earlier (Fig. 2, middle and bottom) (Hollerman and Schultz 1996; Ljungberg et al. 1991, 1992; Mirenowicz and Schultz 1994; Schultz 1986; Schultz and Romo 1990; P. Waelti, J. Mirenowicz, and W. Schultz, unpublished data). The rst dopamine responses to conditioned light were reported by Miller et al. (1981) in rats treated with haloperidol, which increased the incidence and spontaneous activity of dopamine neurons but resulted in more sustained responses than in undrugged animals. Although responses occur close to behavioral reactions (Nishino et al. 1987), they are unrelated to arm and eye movements themselves, as they occur also ipsilateral to the moving arm and in trials without arm or eye movements (Schultz and Romo 1990). Conditioned stimuli are some-

omitted *

rr (Schultz et al. 1997)
FIG .

V V

2. Dopamine neurons report rewards according to an error in reward prediction. Top: drop of liquid occurs although no reward is predicted at this time. Occurrence of reward thus constitutes a positive error in the prediction of reward. Dopamine neuron is activated by the unpredicted

*

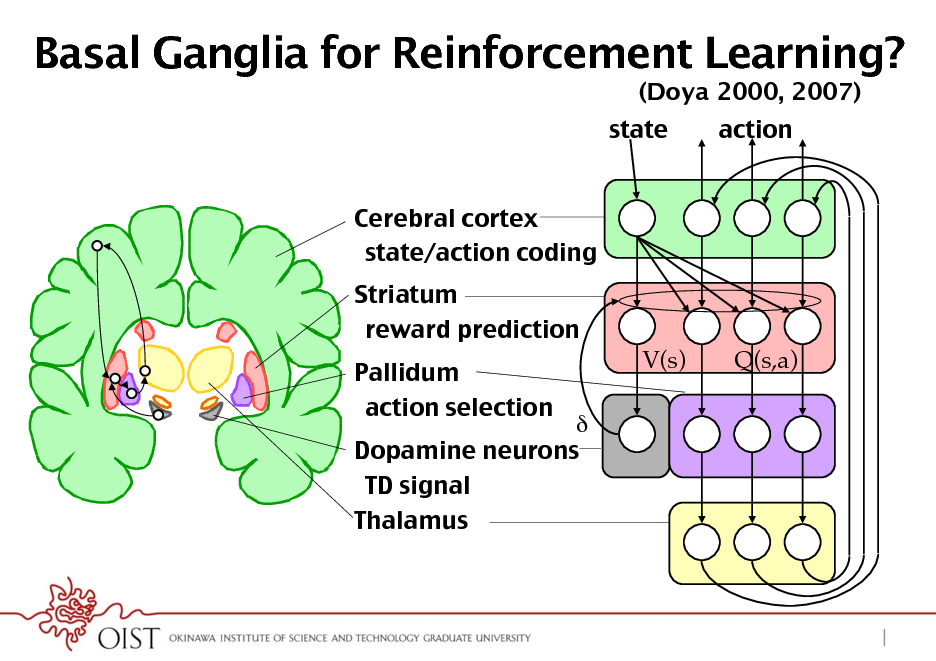
Basal Ganglia for Reinforcement Learning?
(Doya 2000, 2007) state Cerebral cortex! state/action coding! Striatum! reward prediction! Pallidum! action selection! V(s) Q(s,a) action

Dopamine neurons! TD signal! Thalamus!

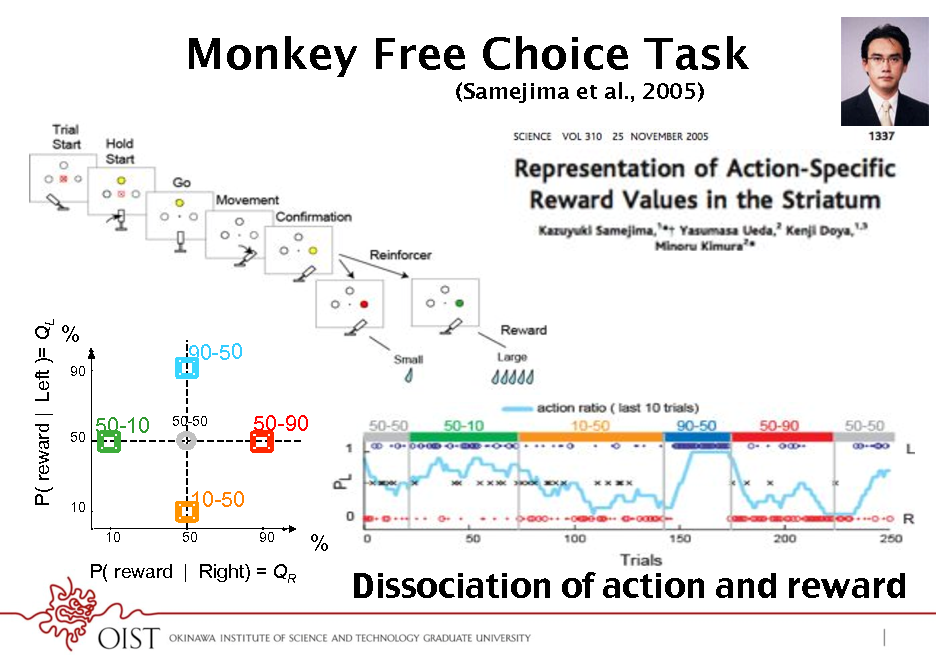
Monkey Free Choice Task
(Samejima et al., 2005)

P( reward | Left )= QL

%
90

90-50

50

50-10

50-50

50-90

10 10

10-50
50 90

%

P( reward | Right) = QR

Dissociation of action and reward!

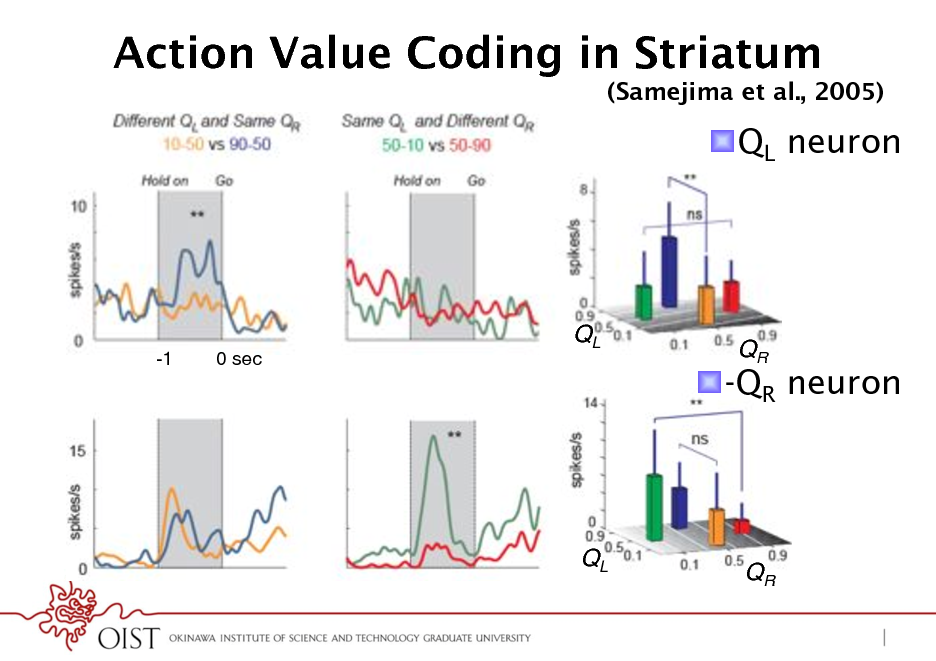
Action Value Coding in Striatum
(Samejima et al., 2005)

! QL neuron

-1

0 sec !

QL !

! -QR neuron

QR !

QL !

QR !

Forced and Free Choice Task
Makoto Ito
0.5-1s 1-2s Center Cue tone Left Right Rwd tone
No-rwd

Left !

Center !

Right !

poking

Pellet

Cue tone Left tone (900Hz)

Reward prob. (L, R) Fixed (50%,0%) Fixed (0%, 50%) Varied (90%, 50%) (50%, 90%) (50%, 10%) (10%, 50%)

pellet dish !

Right tone (6500Hz) Free-choice tone (White noise)

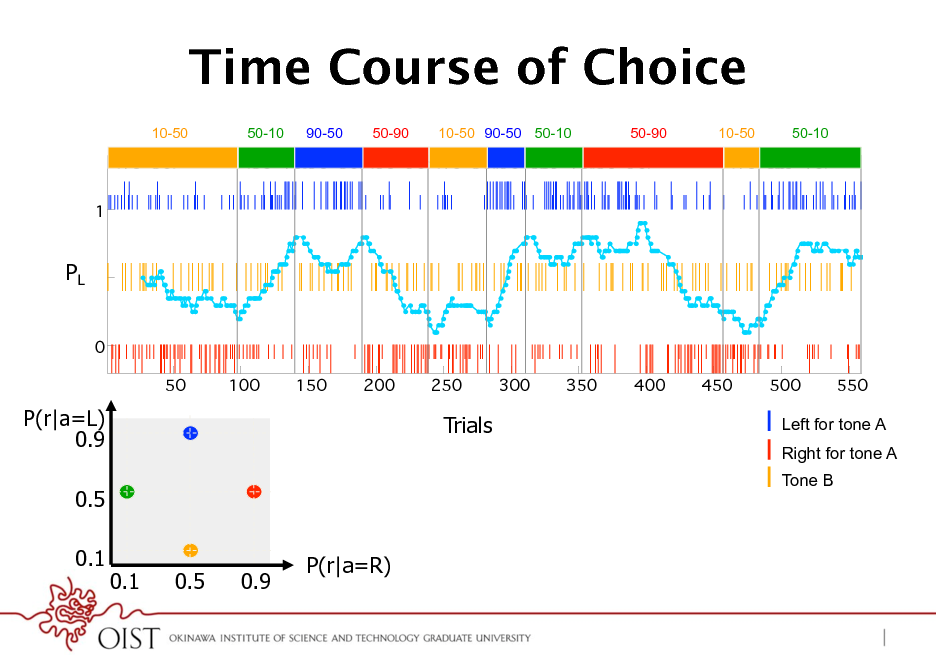
Time Course of Choice
10-50 50-10 90-50 50-90 10-50 90-50 50-10 50-90 10-50 50-10

PL

P(r|a=L) 0.9 0.5 0.1 P(r|a=R)

Trials

Left for tone A Right for tone A Tone B

0.1

0.5

0.9

Generalized Q-learning Model
(Ito & Doya, 2009)

! Action selection P(a(t)=L) = expQL(t)/(expQL(t)+expQR(t)) ! Action value update: i {L,R} Qi(t+1) = (1-1)Qi(t) + 11 if a(t)=i, r(t)=1 (1-1)Qi(t) - 12 if a(t)=i, r(t)=0 (1-2)Qi(t) if a(t)i, r(t)=1 (1-2)Qi(t) if a(t)i, r(t)=0 ! Parameters ! 1: learning rate ! 2: forgetting rate ! 1: reward reinforcement ! 2: no-reward aversion

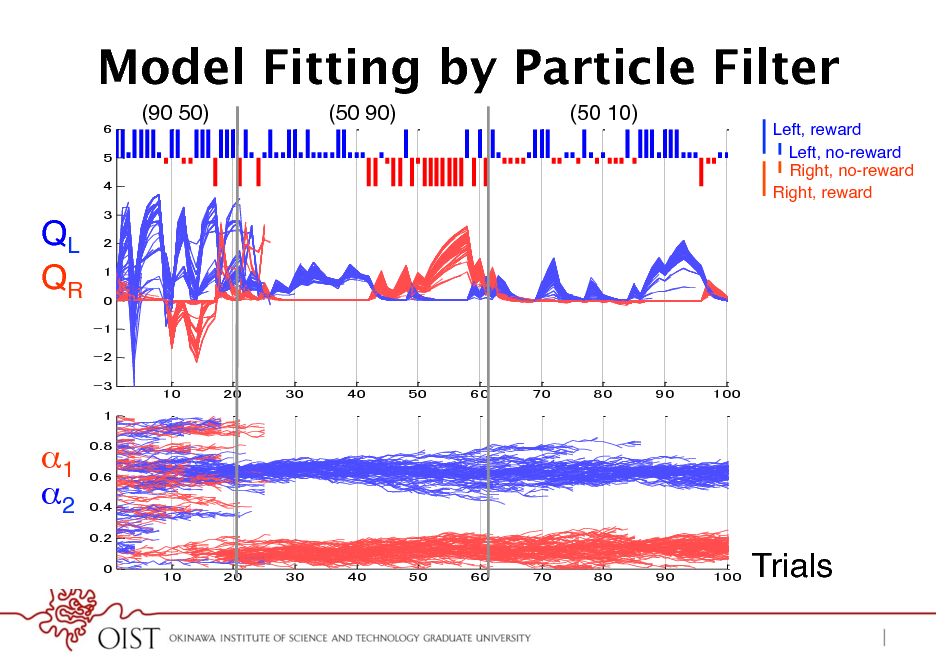
Model Fitting by Particle Filter
(90 50)! (50 90)! (50 10)!
Left, reward! Left, no-reward! Right, no-reward! Right, reward!

QL! QR!

1! 2! Trials!

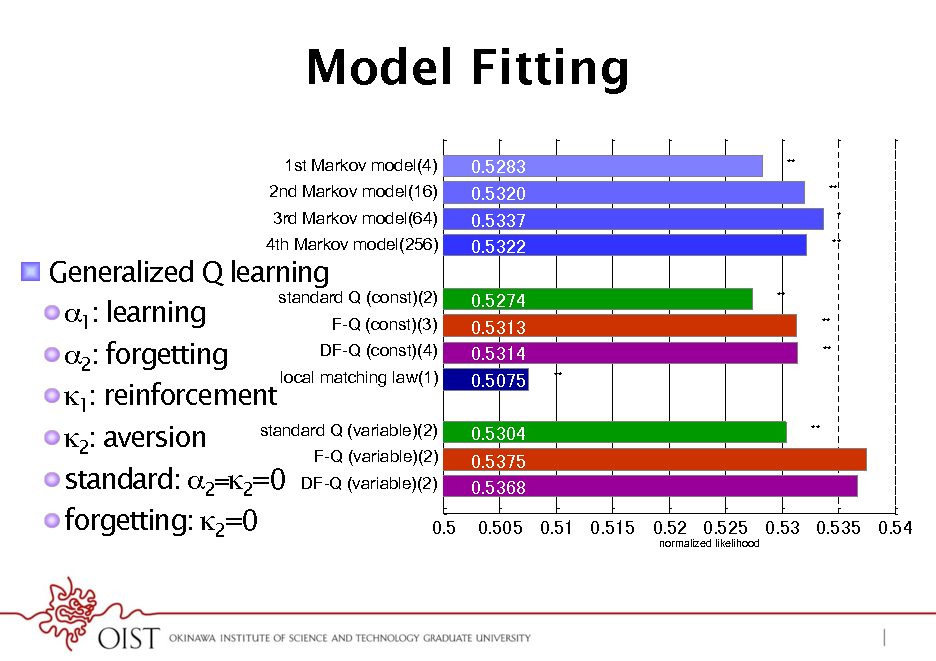
Model Fitting
1st Markov model(4)! 2nd Markov model(16)! 3rd Markov model(64)! 4th Markov model(256)!
**! **! *! **!

! Generalized Q learning standard Q (const)(2)! ! 1: learning F-Q (const)(3)! DF-Q (const)(4)! ! 2: forgetting local matching law(1)! ! 1: reinforcement standard Q (variable)(2)! ! 2: aversion F-Q (variable)(2)! ! standard: 2=2=0 DF-Q (variable)(2)! ! forgetting: 2=0

**! **! **! **!

**!

normalized likelihood!

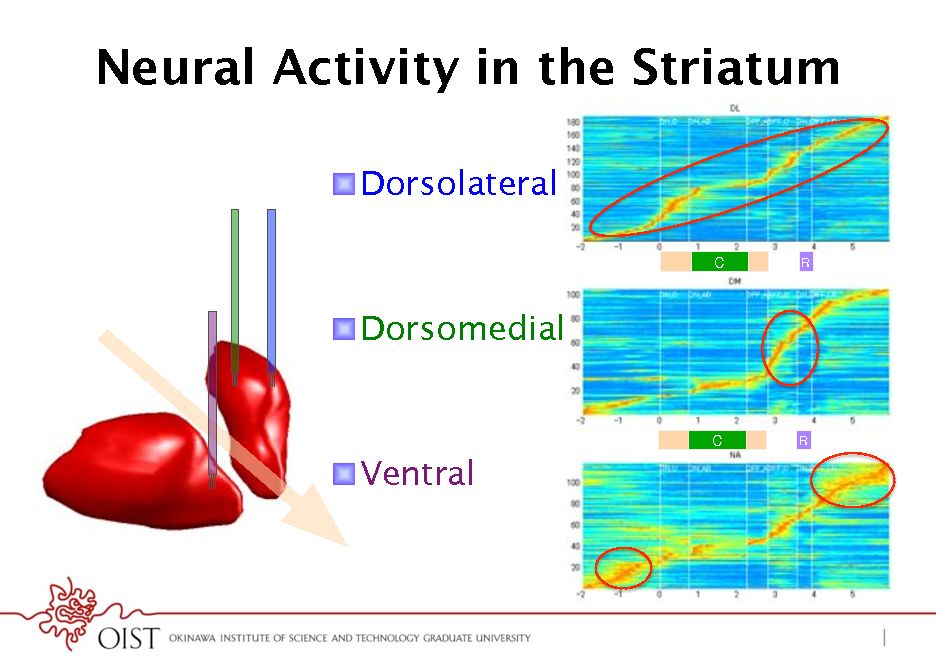
Neural Activity in the Striatum
! Dorsolateral
C!
R!

! Dorsomedial

C!

R!

! Ventral

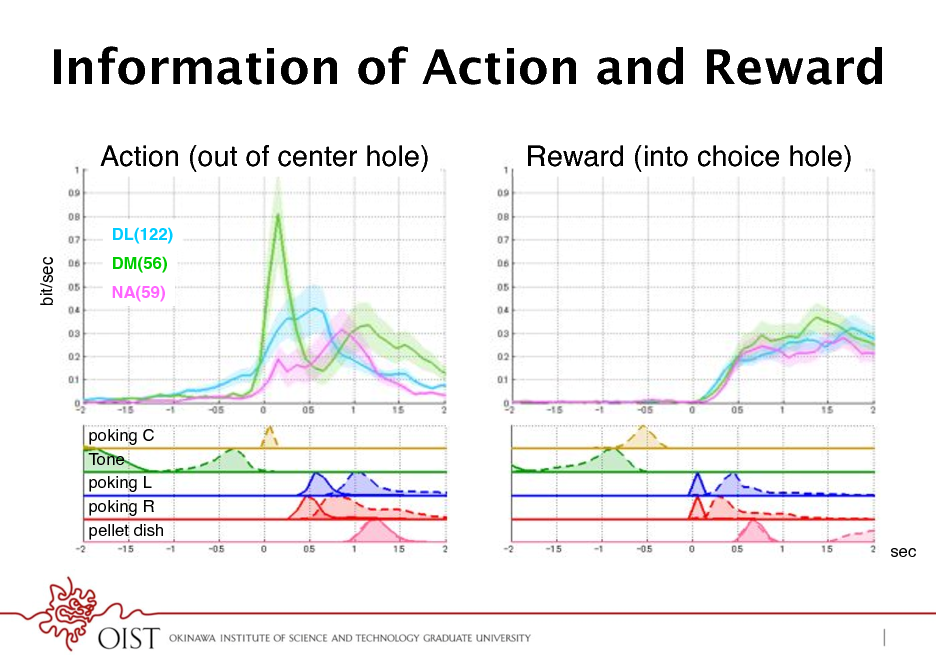
Information of Action and Reward
Action (out of center hole) !
DL(122)!
bit/sec!

Reward (into choice hole) !

DM(56)! NA(59)!

poking C! Tone! poking L! poking R! pellet dish! sec!

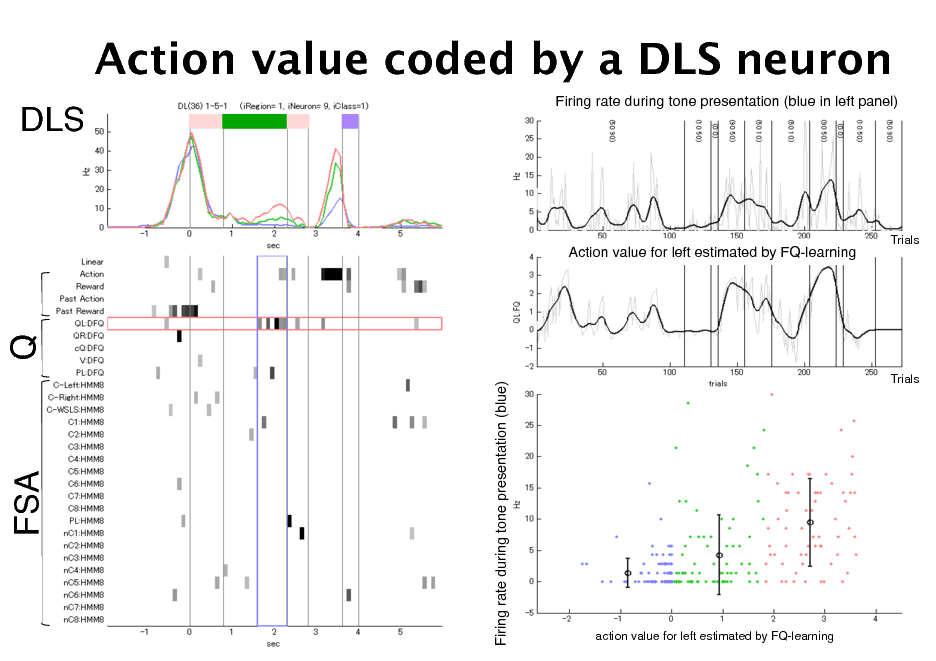
Action value coded by a DLS neuron
DLS!
Firing rate during tone presentation (blue in left panel)!

Action value for left estimated by FQ-learning!

Trials!

Q!

Firing rate during tone presentation (blue)!

Trials!

FSA!

action value for left estimated by FQ-learning!

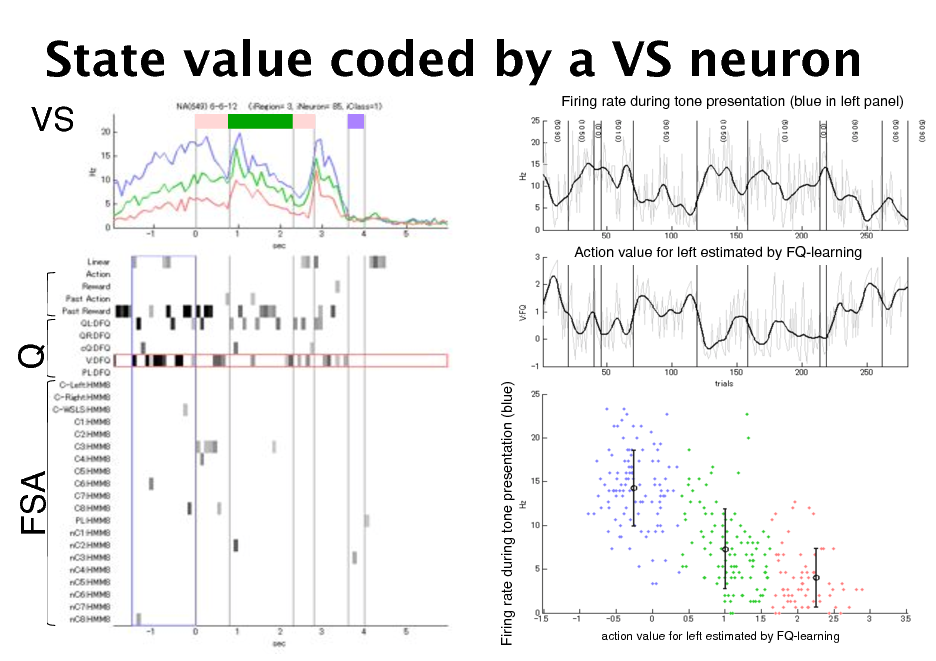
State value coded by a VS neuron
VS!
Firing rate during tone presentation (blue in left panel)!

Action value for left estimated by FQ-learning!

Q!

Firing rate during tone presentation (blue)!

FSA!

action value for left estimated by FQ-learning!

Hierarchy in Cortico-Striatal Network
! Dorsolateral striatum motor ! early action coding ! what action to take? ! Dorsomedial striatum - frontal ! action value ! in what context? ! Ventral striatum - limbic ! state value ! whether worth doing?

(Voorn et al., 2004)!

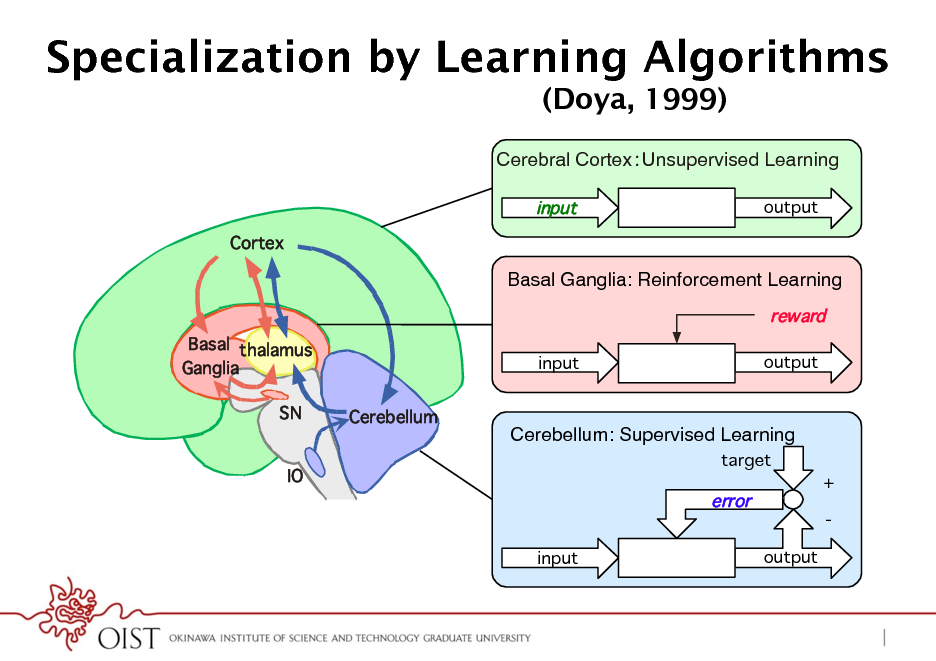
Specialization by Learning Algorithms
(Doya, 1999)
Cerebral CortexUnsupervised Learning!
input
Cortex output

Basal Ganglia: Reinforcement Learning!
reward
Basal thalamus Ganglia SN Cerebellum input output

Cerebellum: Supervised Learning!
target

IO

error
input output

+ -

Multiple Action Selection Schemes
! Model-free ! a = argmaxa Q(s,a) ! Model-based ! a = argmaxa [r+V(f(s,a))] forward model: f(s,a) ! Lookup table a ! a = g(s)
a Q a ai s V f s s s

g

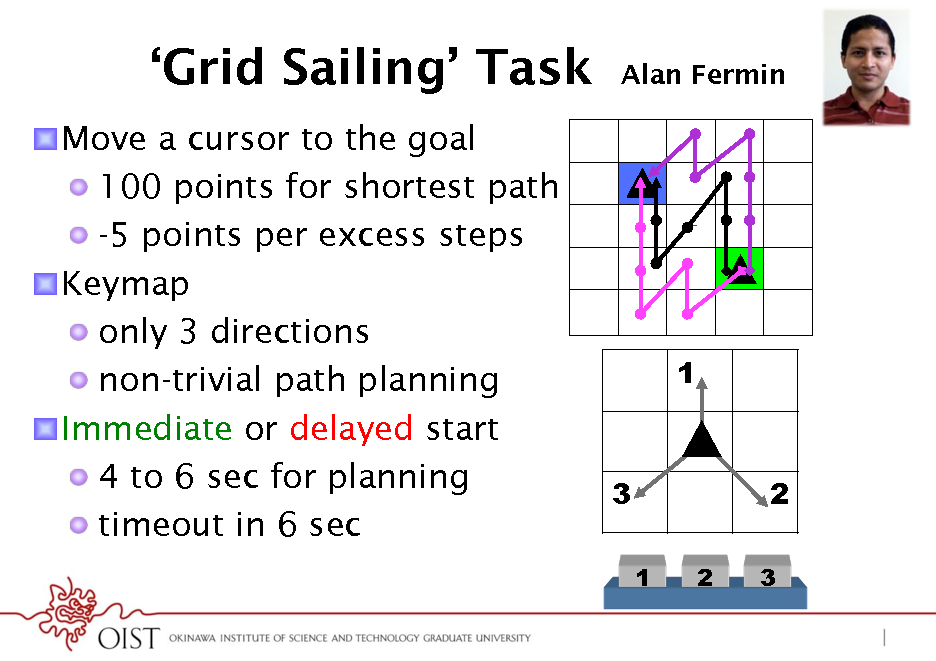
Grid Sailing Task
! Move a cursor to the goal ! 100 points for shortest path ! -5 points per excess steps ! Keymap ! only 3 directions ! non-trivial path planning ! Immediate or delayed start ! 4 to 6 sec for planning ! timeout in 6 sec

Alan Fermin

+

1

3
1 2

2
3

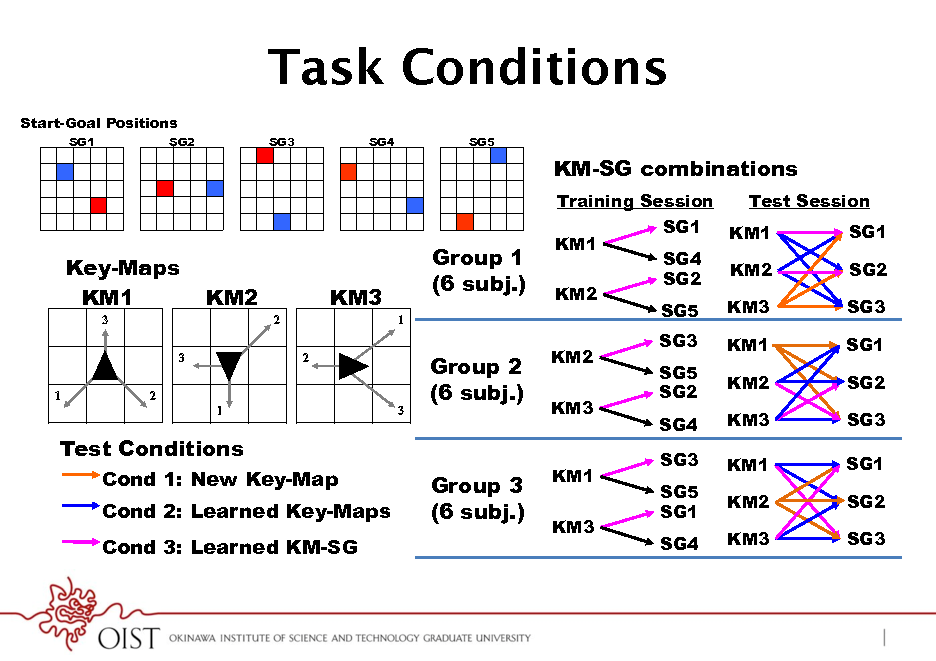
KM3 SG3 SG4 Q>=A89H;<R)B=?7)>C<):>8=>)Q=<GR)>?)>C<)>8=H<>)H?8;)QE;6<R)EF):<_6<9>A8;;F)K=<::A9H) Test Conditions SG3 SG1 KM1 >C=<<)I<F:M)Y9:>=6@>A?9)J8:)>?);<8=9)8):A9H;<)?K>A78;)8@>A?9):<_6<9@<)Q:C?=><:>) KM1 Cond 1: New Key-Map Group 3 SG5 SG2 KM2 SG1 Cond 2: Learned Key-Maps (6 subj.) K8>CJ8FR)B?=)<8@C)?B)>C<)124*!)K8A=:D)JCA@C)J<=<)@?9:>89>)>C=?6HC?6>)>C<) KM3 KM3 SG3 SG4 Cond 3: Learned KM-SG <LK<=A7<9>M)/C<):>8=>)K?:A>A?9)@?;?=):K<@ABA<G)JC<>C<=)>?):>8=>)8)=<:K?9:<) Start-Goal Positions A77<GA8><;F)?=)8B><=)8)G<;8F)Q`:<@RM

Task Conditions
SG3 SG4 SG5

SG1

SG2

Buttons & Fingers
1 2 3 INDEX MIDDLE RING

KM-SG combinations
Training Session
Test Schedule
TB1

Test Session SG1
2400 2200 2000 1800 1600 1400 1200 1000 800 600 400 200 0 A-2 A-1 A-1 A-3 A-3

Reaction Time (ms)

TB1

4 trials 4 trials 4 trials 4 trials
=<<:F=8G: F:78L:F =<<:F=8G: F:78L:F

Random Random Random Random 9 trials 9 trials 9 trials 9 trials
=<<:F=8G: F:78L:F =<<:F=8G: F:78L:F

KM3
2

TB2

KM2 KM2 KM3

SG5 SG3 SG5 SG2
15 10

KM3 KM1
5 0

Reaction Time (ms)

Key-Maps 240 trials TB2 TB3 KM1 Random Random KM2 Random Random
1 2 19 20

Training Schedule

Group 1 180 trials (6 subj.)
9 10

KM1

SG1 KM1 !"#$%&'()*$+,-./&'0)1234*!(
2400 2200 2000 1800 1600 1400 1200 1000 800 600 400 200 0 A-2 A-1 A-1 A-3 A-3

SG4 SG2

KM2

SG2 SG3 SG1
15 10 5

1

Sequence of Trial Events
IMMEDIATE ITI DELAY

Group 2 No Reach Reward (6 subj.)
T

Action Sequence

Trial

KM2 KM3 KM1 KM2 KM3

Action Sequence

SG2

Trial

S S
Goal Reach

S
U

Test Conditions
S S
3~5 sec 4~6 sec

SG4 SG3 SG5 SG1 SG4

Cond 1: New Key-Map
6 sec

Cond 2: Learned Key-Maps Cond 3: Learned KM-SG

S

Time-over: 0 Fail: -5 Optimal: 100

Group 3 >U S (6 subj.) VU
2 sec

KM1 KM3

e<)@?9BA=7<G)>C<) SG3 B?=78>A?9)?B)C8EA> A9)8;;)K<=B?=789@< 8@_6A:A>A?9)89G)8)G SG1 =<8@C)>C<)>8=H<>)H? BA9A:C)89)8@>A?9):<_ SG2 8;:?)?E:<=O<G)A9)>C SG3 89G)8B><=)?9<)9AHC

Start-Goal Positions
SG1 SG2 SG3 SG4 SG5

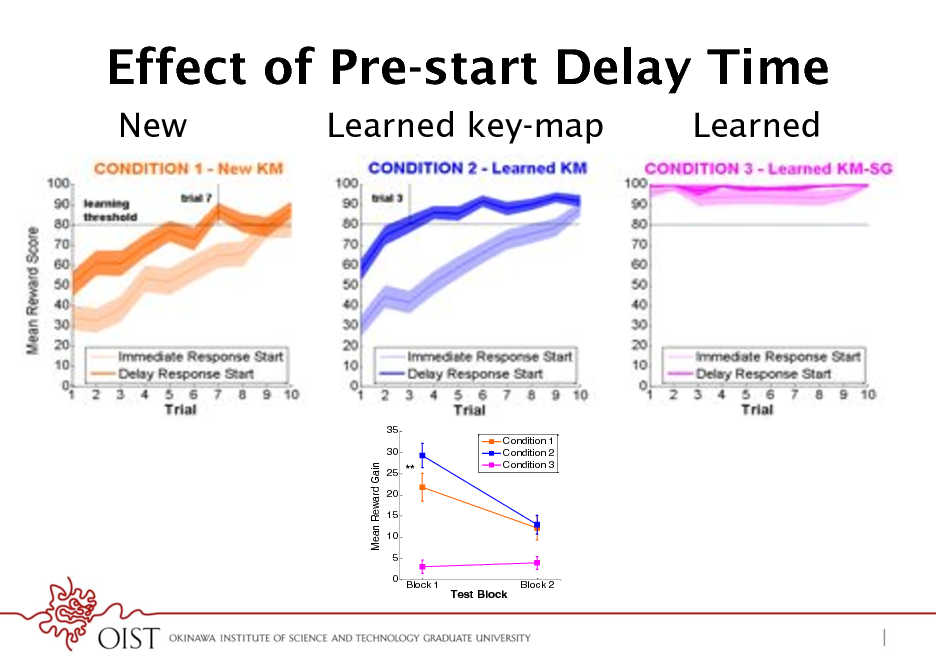
Effect of Pre-start Delay Time
New Learned key-map Learned

35 30 Condition 1 Condition 2 Condition 3

100 90 80

100 90

% Optimal Goal Reach

Mean Reward Gain

% Reward Score

25 ** 20 15 10 5 0 Block 1

80 70 60 50 40 30 20 10 0 1

70 60 50 40 30 20 10 0

**

**
Error Suboptimal Optimal

Test Block

Block 2

2

3

4

Trial Type

Trial

5

6

7

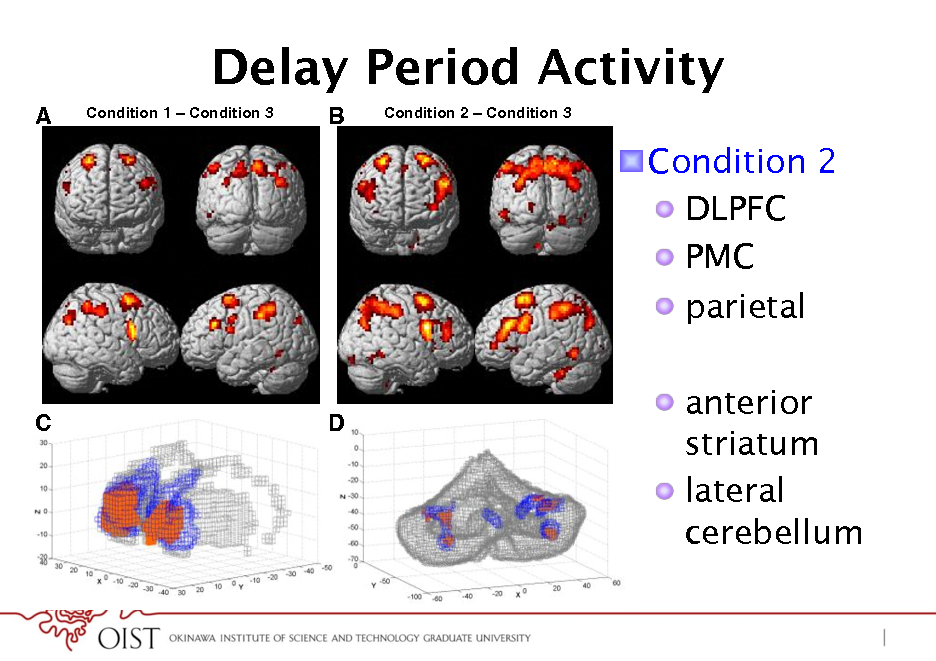
Delay Period Activity
A
Condition 1 Condition 3

B

Condition 2

Condition 3

! Condition 2 ! DLPFC ! PMC ! parietal ! anterior striatum ! lateral cerebellum

C

D

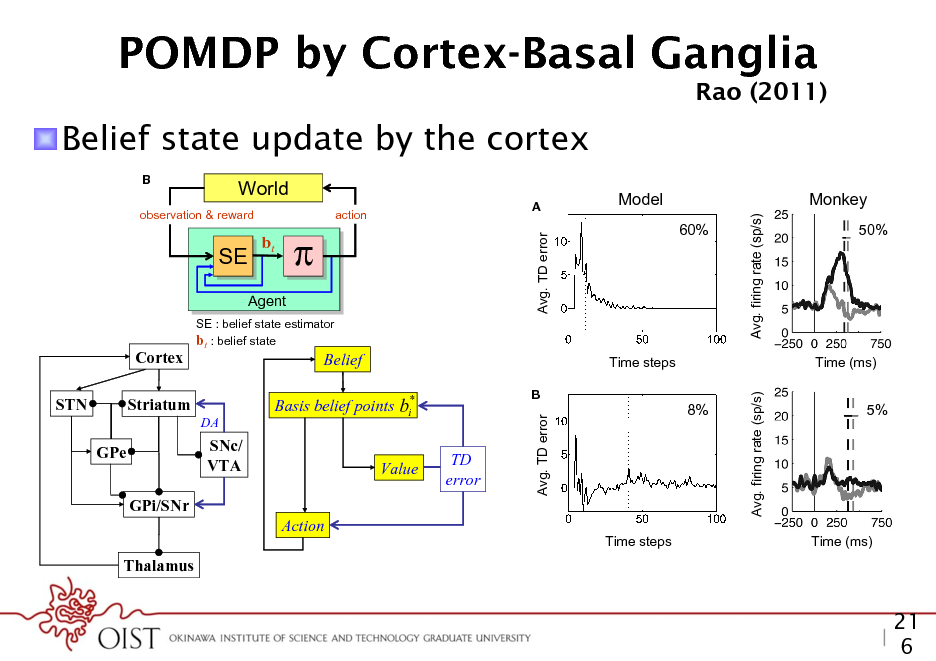
POMDP by Cortex-Basal Ganglia
Decision making under uncertainty

Rao (2011)
Rao

! Belief state update by the cortex
B

(s,a,s)

World
action

Rao

SE SE

bt

Avg. TD error

60%

Avg. firing rate (sp/s)

observation & reward

A

Model

Monkey
50%

Action a

Decision makin

nt

Agent
SE : belief state estimator bt : belief state

Cortex

Belief

t the space of beliefs ate vector is a prob1 nsional (number of describing the feedforward transformation of the input, M is the GPi/SNr es). This makes the matrix of recurrent synaptic weights, and g1 is a dendritic ltering Action ult. In fact, nding function. has been proved to The above differential equation can be rewritten in discrete nite-horizon case is Thalamus form as: 1987). However, one of which work | Suggested mapping of elements of the model to components FIGURE 3 well v t (i ) f (ot ) g M (i , j )v t 1( j ) (4) o a popular class of j of the cortex-basal ganglia network. STN, subthalamic nucleus; GPe, globus ed POMDP solvers pallidus, external segment; GPi, Globus pallidus, internal segment; SNc,

GPe

SNc/ TD VTA where v denotes the vector of output ring rates, o denotes the Value error input observation vector, f is a potentially non-linear function

Avg. TD error

b

Avg. firing rate (sp/s)

ecutes an action a in the e s according to the STN ervation o of the new der to solve the POMDP

problem, the animal maintains a belief bt which is a probability distribution over states of the world. This belief is computed iteratively using Bayesian inference * Striatum Basis for the points step is provided by by the belief state estimator SE. An actionbeliefcurrent time i DA the learned policy , which maps belief states to actions.

We model the task using a POMDP as follow Time steps Time (ms) underlying hidden states representing the two possi coherent motion (leftward or rightward). In each t B 8% menter chooses one of these hidden states5% (either le ward) and provides the animal with observations state in the form of an image sequence of random do coherence. Note that the hidden state remains the sa of the trial. Using only the sequence of observed im the animal must choose one of the following actio Time steps Time (ms) more time step (to reduce uncertainty), make a left FIGURE 16 | Reward predictionchoice dopamine responses in the ment (indicating error and of leftward motion), or m random dots task. (A) The plot on the left shows the temporal evolution of eye movement (indicating choice of rightward mo reward prediction (TD) error in the model, averaged over trials with Easy motion coherence (coherence = 60%). The dotted line shows the average We use the notation SL to represent the21 state reaction time. The plot on the right shows the average ring rate of dopamine neuronsleftward motion and random dots task at 50% motion 6 to in SNc in a monkey performing the S to represent rightward

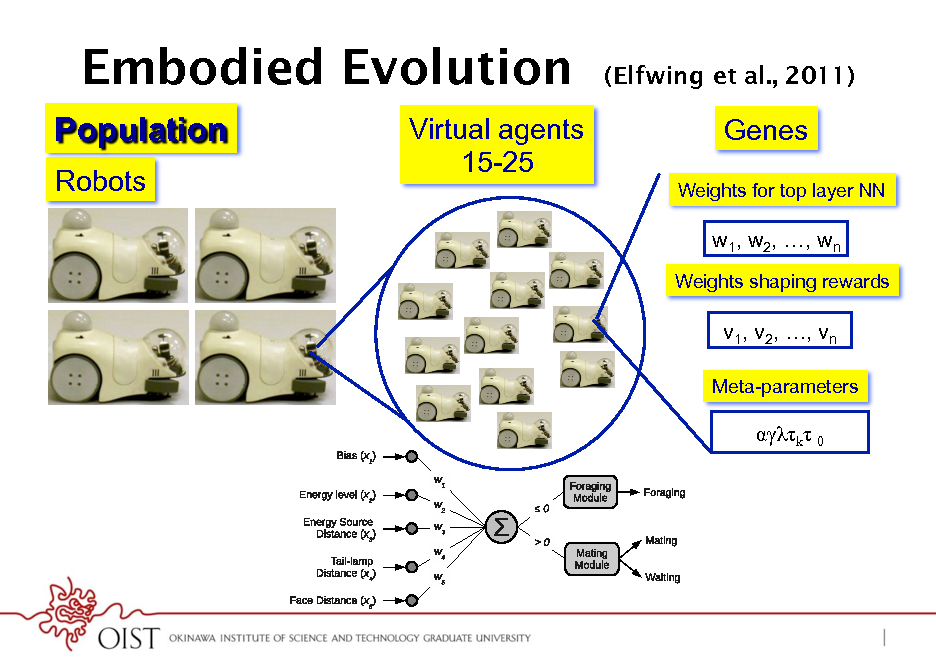
Embodied Evolution
Population
Robots Virtual agents 15-25

13

(Elfwing et al., 2011)

Genes
Weights for top layer NN

w1, w2, , wn
Weights shaping rewards

v1, v2, , vn
Meta-parameters
(a)

k 0

(b)

Temporal Discount Factor *
! Large ! reach for far reward* ! Small ! only to near reward*

Temporal Discount Factor *
! V(t) = E[ r(t) + r(t+1) + 2r(t+2) + 3r(t+3) +] ! controls the character of an agent
large
1 no pain, no gain! V =18.7 0 -20 -20 -20 1 1 stay away from danger 0 V = -22.9 +50 1 2 -100 3 4 step 2 3 4 step 1 0 +50 1 2 -100 3 4 step +100 1 0 -20 -20 -20 1 2 3 4 step

small
+100

Depression?!
better stay idle V =-25.1

Impulsivity?!
cant resist temptation V = 47.3

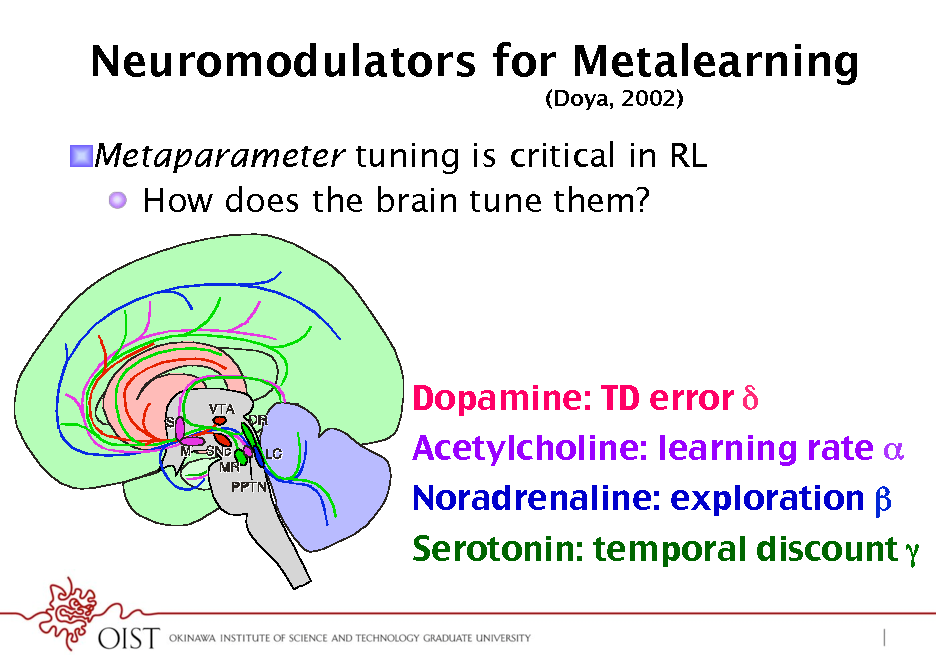
Neuromodulators for Metalearning
(Doya, 2002)

! Metaparameter tuning is critical in RL ! How does the brain tune them?

Dopamine: TD error ! Acetylcholine: learning rate ! Noradrenaline: exploration Serotonin: temporal discount !

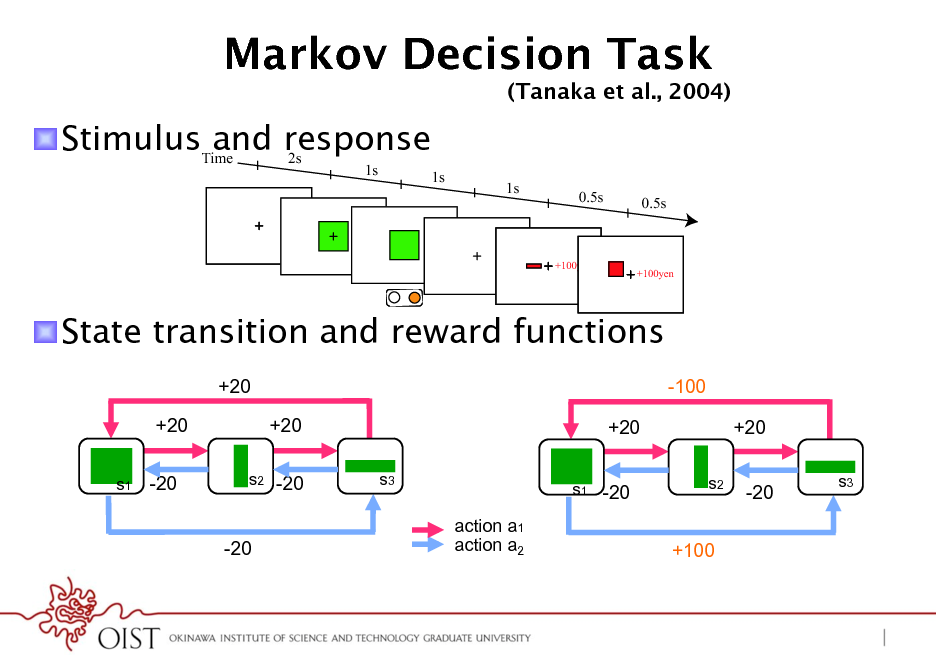
Markov Decision Task
! StimulusTime response and 2s
1s 1s 1s 0.5s 0.5s

(Tanaka et al., 2004)

+100yen

+100yen

! State transition and reward functions
+20 +20
s1 -20

-100 +20 +20
s3 s1 -20 s2

+20 -20
s3

s2 -20

-20

action a1 action a2

+100

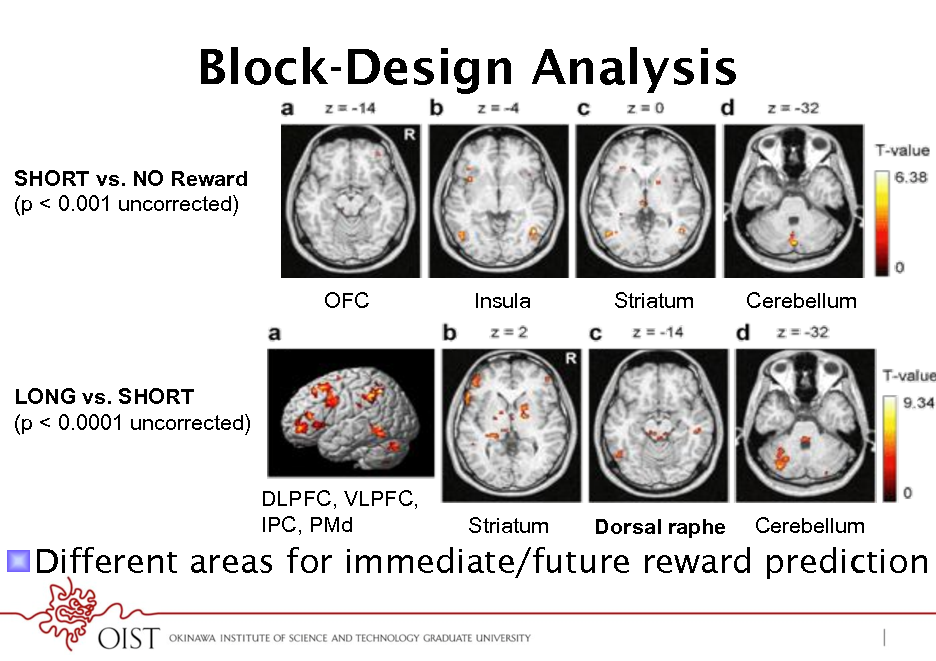
Block-Design Analysis
SHORT vs. NO Reward (p < 0.001 uncorrected)

OFC

Insula

Striatum

Cerebellum

LONG vs. SHORT (p < 0.0001 uncorrected) DLPFC, VLPFC, IPC, PMd

Striatum

Dorsal raphe

Cerebellum

! Different areas for immediate/future reward prediction

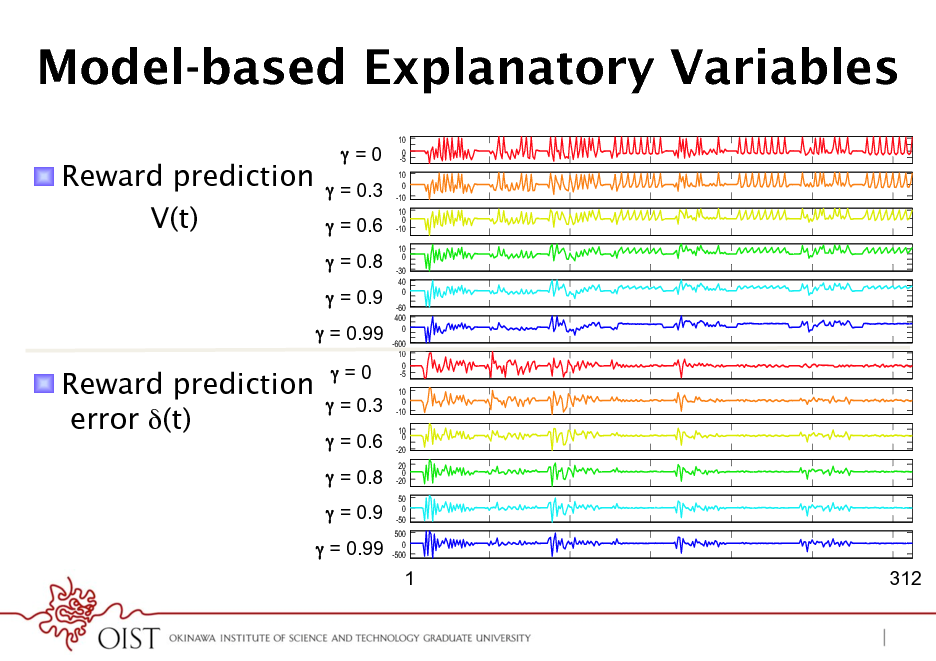
Model-based Explanatory Variables
! Reward prediction V(t)
=0 = 0.3 = 0.6 = 0.8 = 0.9 = 0.99
10 0 -5 10 0 -10 10 0 -10 10 0 -30 40 0 -60 400 0 -600 10 0 -5 10 0 -10 10 0 -20 20 0 -20 50 0 -50 500 0 -500

V V V V V

! Reward prediction error (t)

=0 = 0.3 = 0.6 = 0.8 = 0.9 = 0.99

delta delta delta delta delta

1

trial

312

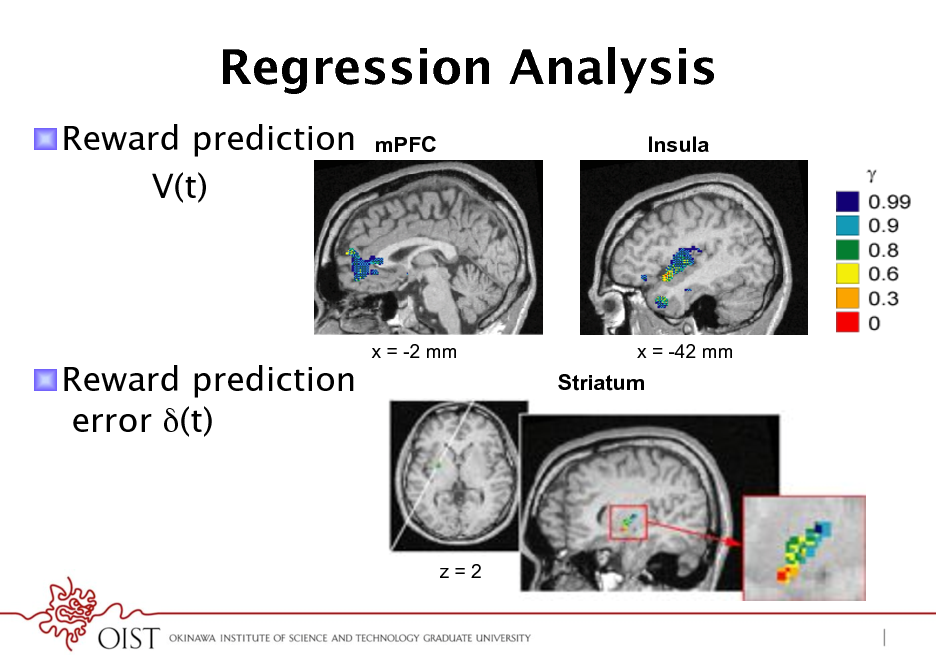
Regression Analysis
! Reward prediction V(t)
mPFC Insula

! Reward prediction error (t)

x = -2 mm

x = -42 mm

Striatum

z=2

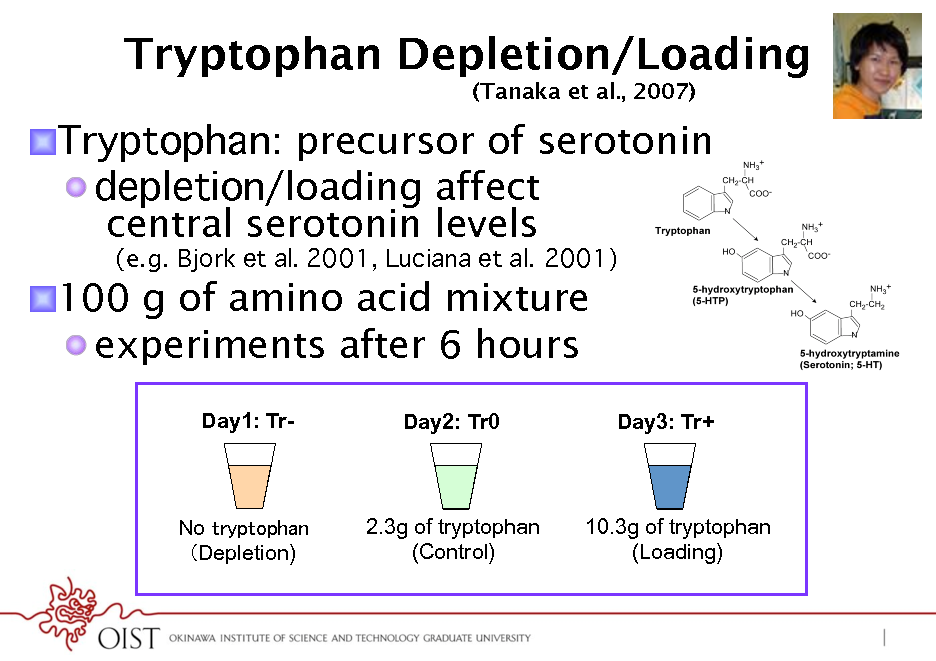
Tryptophan Depletion/Loading
(Tanaka et al., 2007)

! Tryptophan: precursor of serotonin ! depletion/loading affect central serotonin levels
(e.g. Bjork et al. 2001, Luciana et al. 2001)

! 100 g of amino acid mixture ! experiments after 6 hours
Day1: TrDay2: Tr0

Day3: Tr+

No Depletion)

2.3g of tryptophan (Control)

10.3g of tryptophan (Loading)

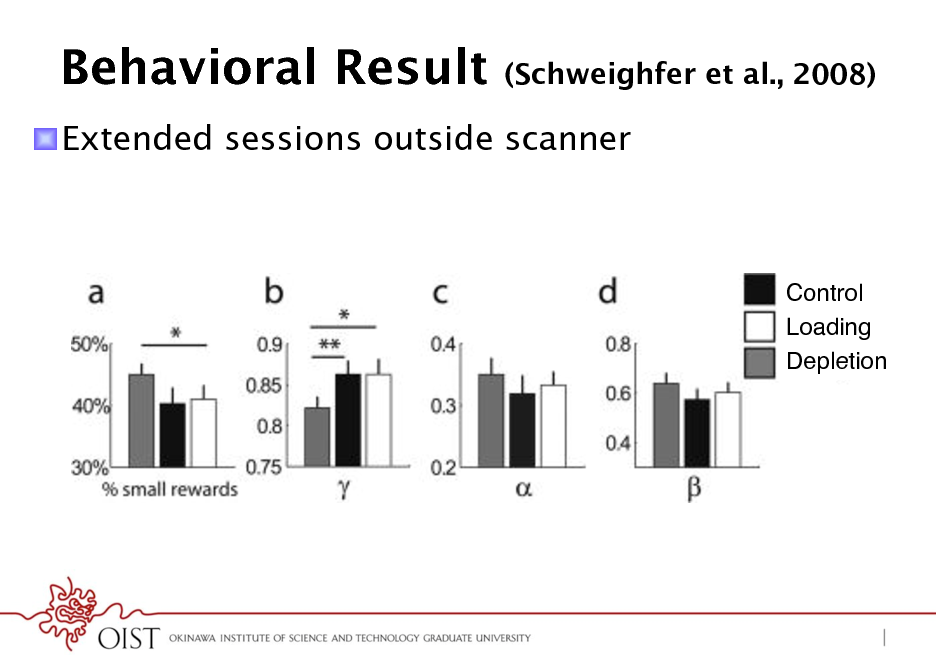
Behavioral Result

(Schweighfer et al., 2008)

! Extended sessions outside scanner

Control! Loading! Depletion!

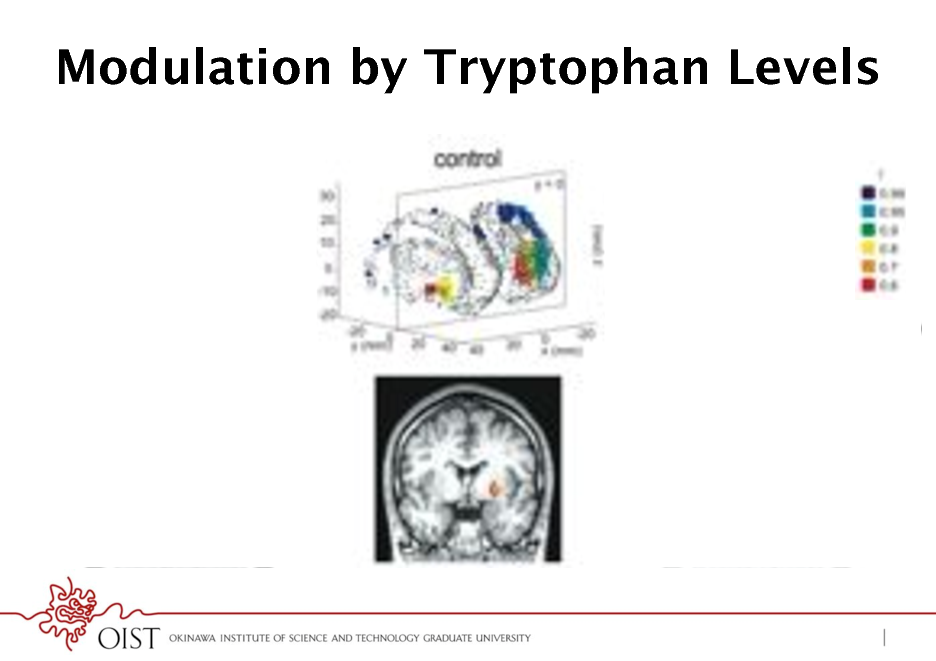
Modulation by Tryptophan Levels

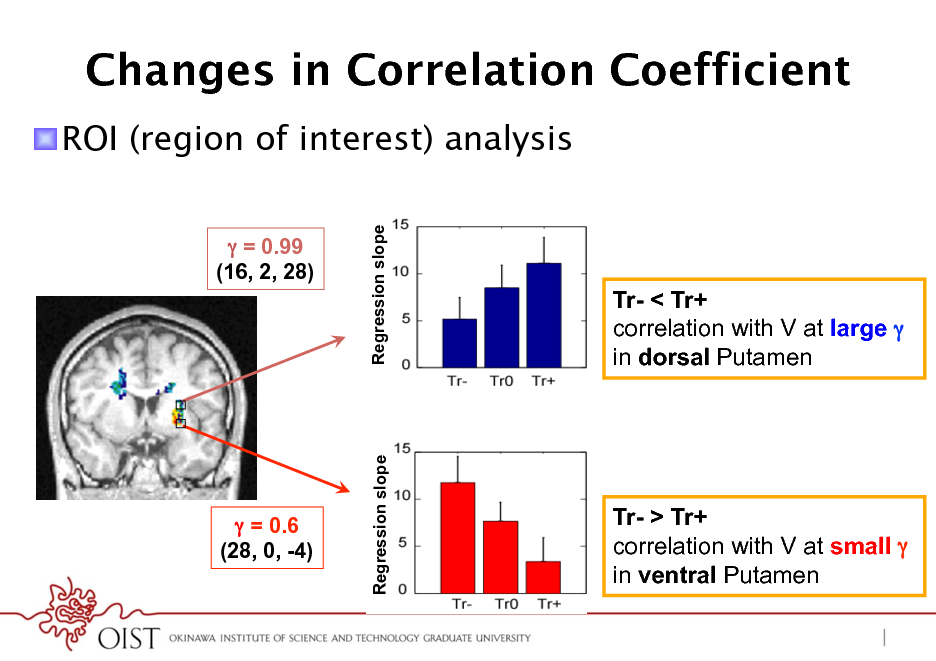
Changes in Correlation Coefficient
! ROI (region of interest) analysis
= 0.99 (16, 2, 28)
Regression slope

Tr- < Tr+ correlation with V at large in dorsal Putamen

Regression slope

= 0.6 (28, 0, -4)

Tr- > Tr+ correlation with V at small in ventral Putamen

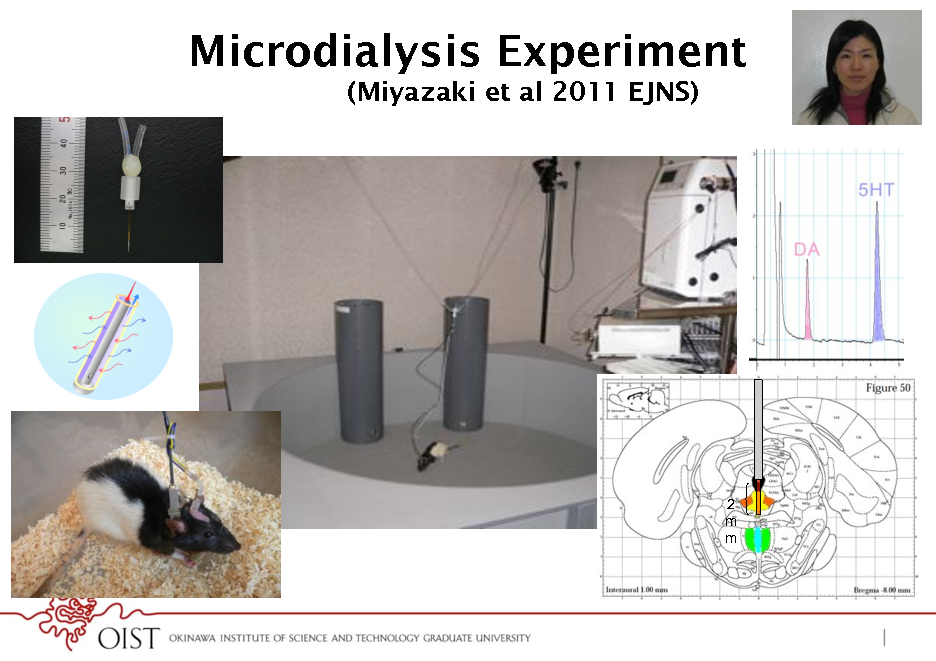
Microdialysis Experiment
(Miyazaki et al 2011 EJNS)

2 m m

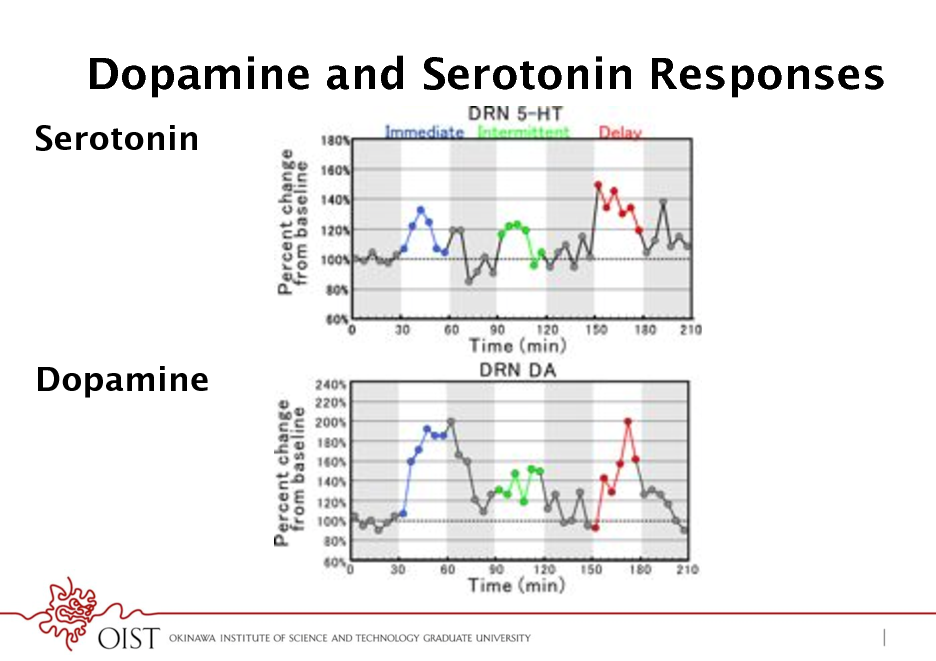
Dopamine and Serotonin Responses
Serotonin

Dopamine

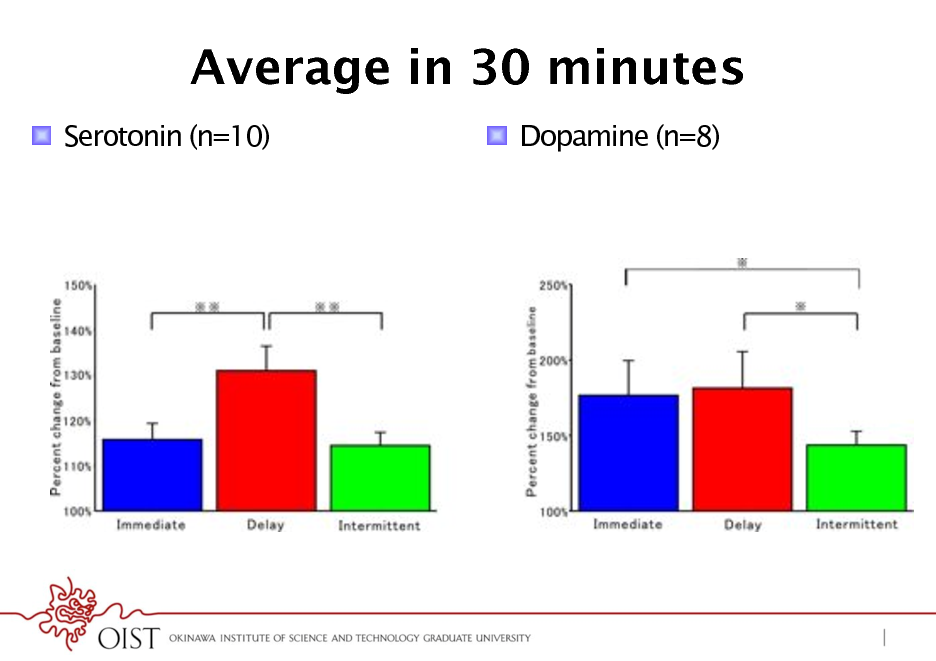
Average in 30 minutes
! Serotonin (n=10) ! Dopamine (n=8)

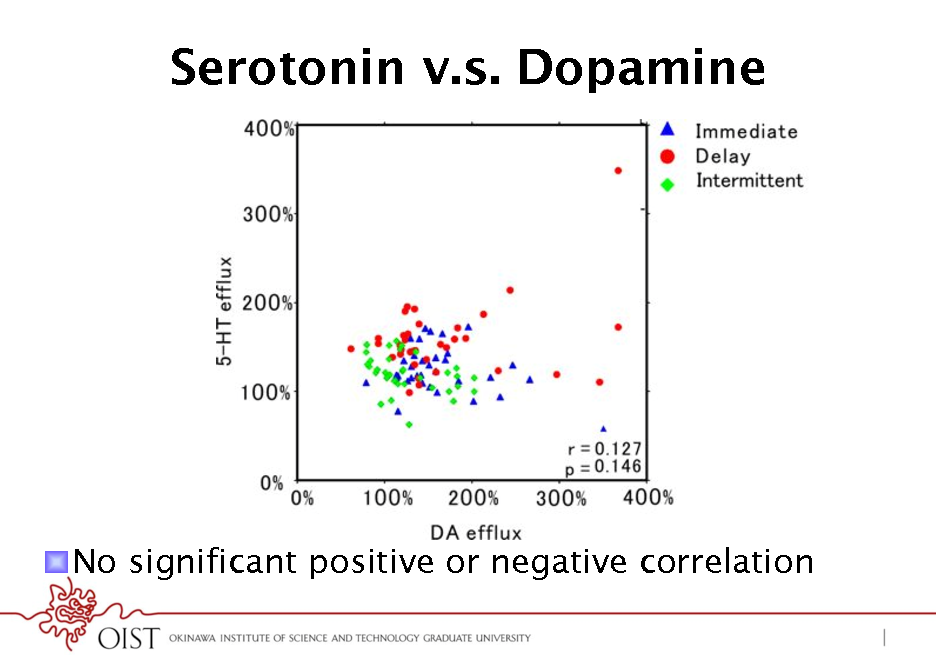
Serotonin v.s. Dopamine
Immediate Delayed Intermittent

! No significant positive or negative correlation

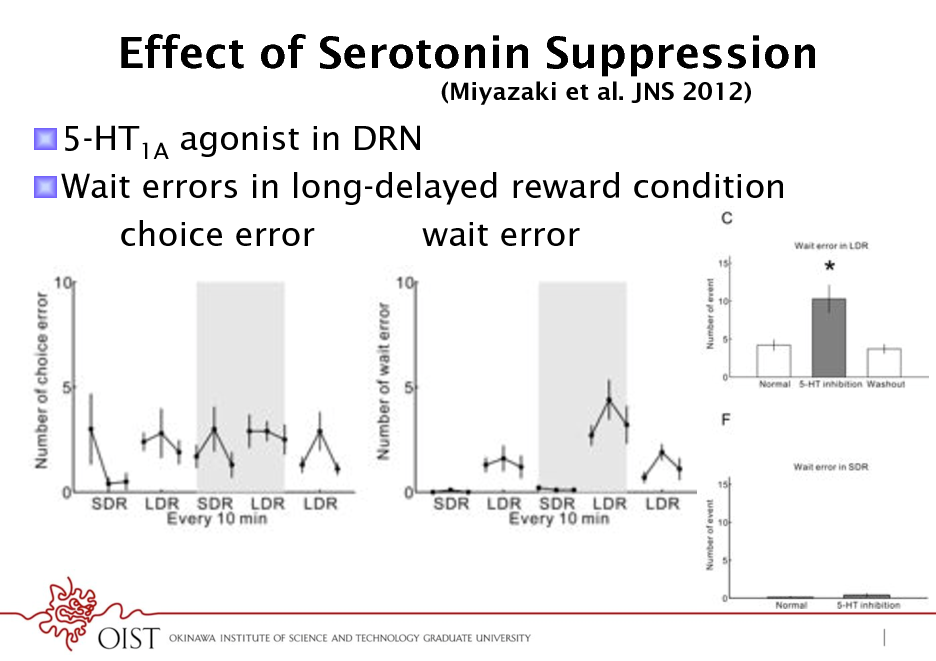
Effect of Serotonin Suppression
(Miyazaki et al. JNS 2012)

! 5-HT1A agonist in DRN ! Wait errors in long-delayed reward condition choice error wait error

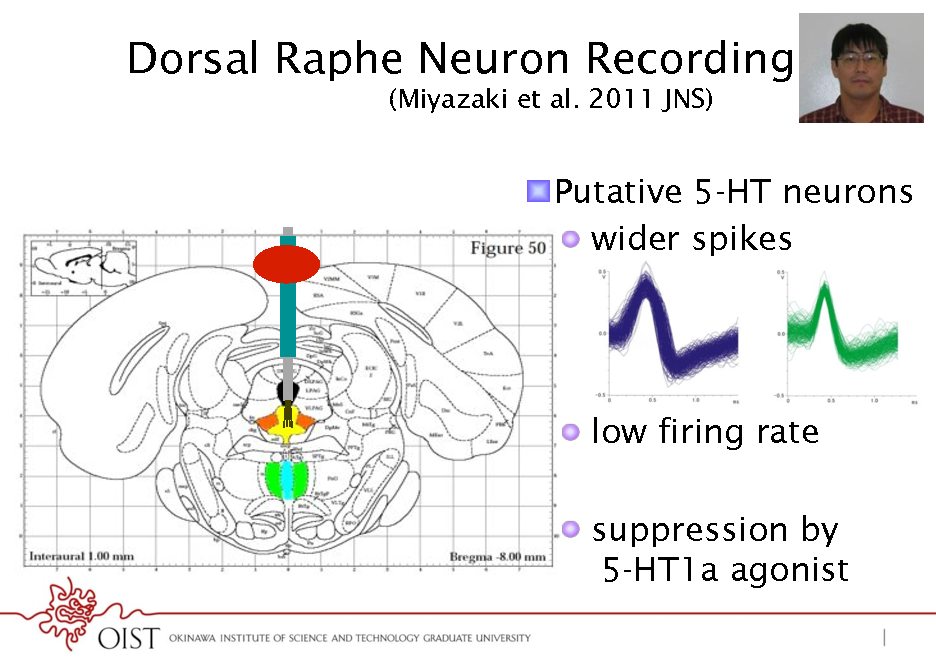
Dorsal Raphe Neuron Recording (Miyazaki et al. 2011 JNS)
! Putative 5-HT neurons ! wider spikes

! low firing rate ! suppression by 5-HT1a agonist

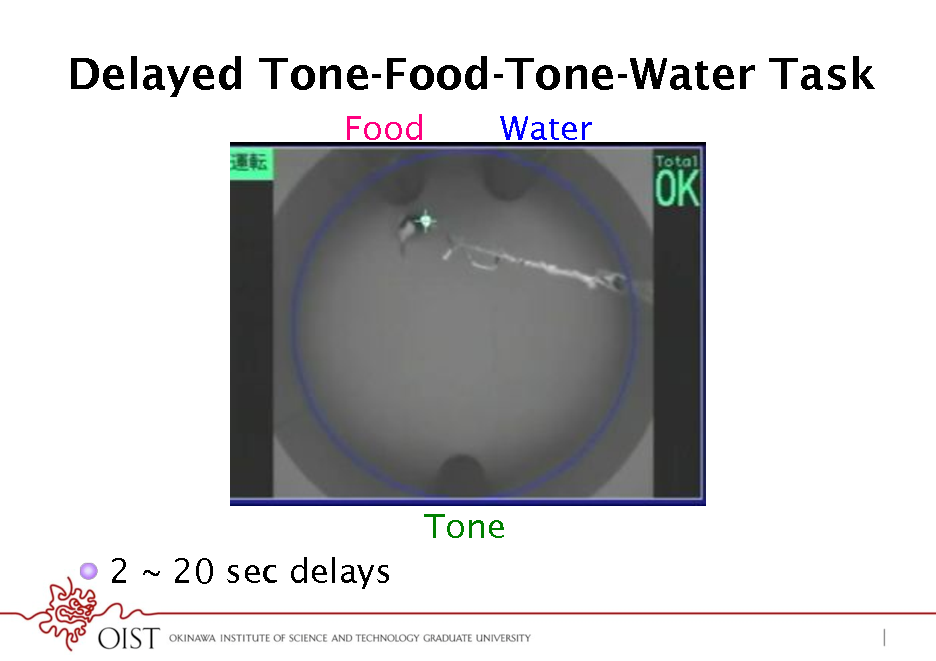
Delayed Tone-Food-Tone-Water Task
Food Water

Tone ! 2 ~ 20 sec delays

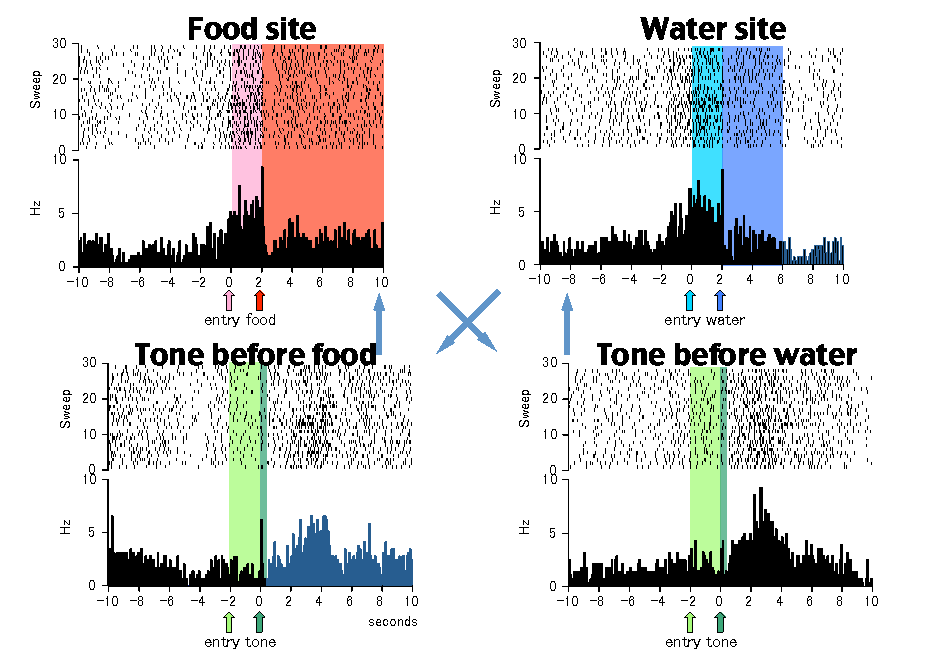
Food site!

Water site!

Tone before food!

Tone before water!

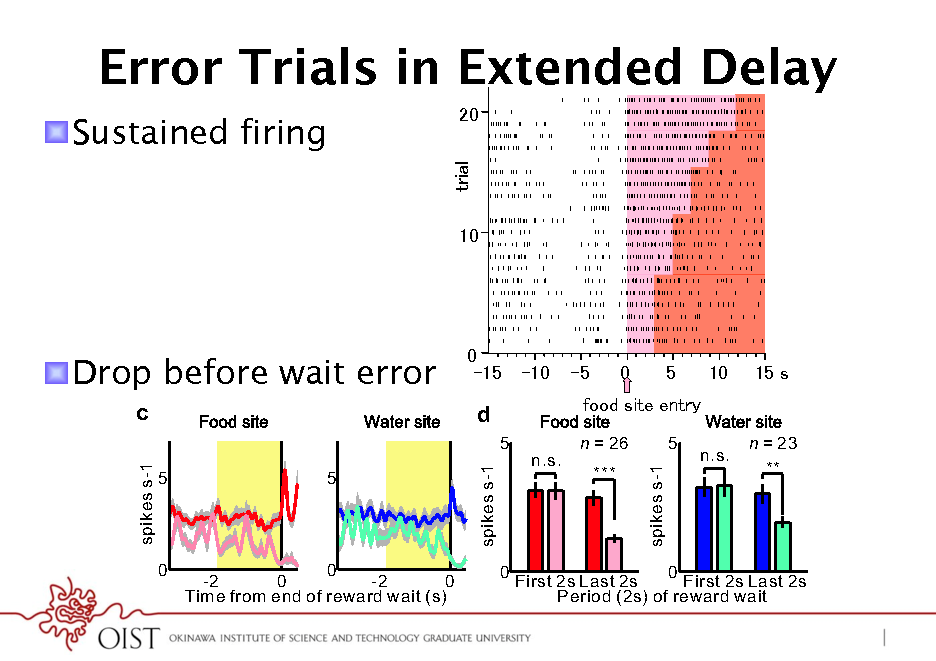
Error Trials in Extended Delay
0 0 5 Time (s) 0 5 10 Time (s) 15 0 0 5 Time (s) 0 5 10 Time (s) 15

! SustainedTone site firing b
Trial
10

Food site

Tone site

Water site

0

Trial
0 5 Time (s) 0 5 Time (s)

10

0

! Drop before wait error
c
spikes s-1
5 5

0

5 Time (s)

0 5 Time (s)

d
5 n = 26 5

spikes s-1

***

0

0 -2 0 -2 0 Time from end of reward wait (s)

0

0 First 2s Last 2s First 2s Last 2s Period (2s) of reward wait

e

spikes s-1

n.s.

n.s.

n = 23 **

Serotonin Experiments: Summary
! Microdialysis ! higher release for delayed reward ! no apparent opponency with dopamine ! lower release cause waiting error Consistent with discounting hypothesis ! Serotonin neuron recording ! higher firing during waiting ! firing stops before giving up More dynamic variable than a parameter ! Question: regulation of serotonin neurons ! algorithm for regulation of patience

Collaborators
! ATR Tamagawa U ! Kyoto PUM ! Kazuyuki Samejima ! Minoru Kimura ! NAISTCalTechATROsaka U ! Yasumasa Ueda ! Saori Tanaka ! Hiroshima U ! CREST USC ! Shigeto Yamawaki ! Nicolas Schweighofer ! Yasumasa Okamoto ! OIST ! Go Okada ! Makoto Ito ! Kazutaka Ueda ! Kayoko Miyazaki ! Shuji Asahi ! Katsuhiko Miyazaki ! Kazuhiro Shishida ! Takashi Nakano ! Jun Yoshimoto ! U Otago OIST ! Eiji Uchibe ! Jeff Wickens ! Stefan Elfwing