Sequential Monte Carlo Methods for Bayesian Computation
A. Doucet
Kyoto

Sept. 2012

A. Doucet (MLSS Sept. 2012)

Sept. 2012

1 / 136

Motivating Example 1: Generic Bayesian Model
Let X be a vector parameter of interest with an associated prior ; i.e. X ( ).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

2 / 136

Motivating Example 1: Generic Bayesian Model
Let X be a vector parameter of interest with an associated prior ; i.e. X ( ).

We observe a realization of y of Y which is assumed to satisfy Y j (X = x ) i.e. the likelihood function is g ( y j x ). g ( j x) ;

A. Doucet (MLSS Sept. 2012)

Sept. 2012

2 / 136

Motivating Example 1: Generic Bayesian Model
Let X be a vector parameter of interest with an associated prior ; i.e. X ( ).

We observe a realization of y of Y which is assumed to satisfy Y j (X = x ) g ( j x) ;

i.e. the likelihood function is g ( y j x ). Bayesian inference on X relies on the posterior of X given Y = y : p (xj y) =
Z

(x ) g ( y j x ) p (y )

where the marginal likelihood/evidence satises p (y ) = (x ) g ( y j x ) dx.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

2 / 136

Motivating Example 1: Generic Bayesian Model
Let X be a vector parameter of interest with an associated prior ; i.e. X ( ).

We observe a realization of y of Y which is assumed to satisfy Y j (X = x ) g ( j x) ;

i.e. the likelihood function is g ( y j x ). Bayesian inference on X relies on the posterior of X given Y = y : p (xj y) =
Z

(x ) g ( y j x ) p (y )

where the marginal likelihood/evidence satises p (y ) = (x ) g ( y j x ) dx.

Machine learning examples: Latent Dirichlet Allocation, (Hiearchical) Dirichlet processes...
A. Doucet (MLSS Sept. 2012) Sept. 2012 2 / 136

Motivating Example 2: State-Space Models
Let fXt gt
1

be a latent/hidden Markov process with X1 ( ) and Xt j (Xt
1

= x)

f ( j x) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

3 / 136

Motivating Example 2: State-Space Models
Let fXt gt
1

be a latent/hidden Markov process with X1 ( ) and Xt j (Xt
1

= x)

Let fYt gt 1 be an observation process such that observations are conditionally independent given fXt gt 1 and Yt j ( Xt = x ) g ( j x) .

f ( j x) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

3 / 136

Motivating Example 2: State-Space Models
Let fXt gt
1

be a latent/hidden Markov process with X1 ( ) and Xt j (Xt
1

= x)

Let fYt gt 1 be an observation process such that observations are conditionally independent given fXt gt 1 and Let zi :j := (zi , zi +1 , ..., zj ) then Bayesian inference on X1:t relies on the posterior of X1:t given Y = y1:t : p ( x1:t j y1:t ) =
Z

f ( j x) .

Yt j ( Xt = x )

g ( j x) .

p (x1:t , y1:t ) p (y1:t )

where the marginal likelihood/evidence satises p (y1:t ) = p (x1:t , y1:t ) dx1:t .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

3 / 136

Motivating Example 2: State-Space Models
Let fXt gt
1

be a latent/hidden Markov process with X1 ( ) and Xt j (Xt
1

= x)

Let fYt gt 1 be an observation process such that observations are conditionally independent given fXt gt 1 and Let zi :j := (zi , zi +1 , ..., zj ) then Bayesian inference on X1:t relies on the posterior of X1:t given Y = y1:t : p ( x1:t j y1:t ) =
Z

f ( j x) .

Yt j ( Xt = x )

g ( j x) .

p (x1:t , y1:t ) p (y1:t )

where the marginal likelihood/evidence satises p (y1:t ) = p (x1:t , y1:t ) dx1:t .

Machine learning examples: Biochemical network models, Dynamic topic models, Neuroscience models etc.
A. Doucet (MLSS Sept. 2012) Sept. 2012 3 / 136

Bayesian Inference and Machine Learning
Bayesian approaches have been adopted by a large part of the ML community.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

4 / 136

Bayesian Inference and Machine Learning
Bayesian approaches have been adopted by a large part of the ML community. Bayesian inference oers a number of attractive advantages over conventional approach

A. Doucet (MLSS Sept. 2012)

Sept. 2012

4 / 136

Bayesian Inference and Machine Learning
Bayesian approaches have been adopted by a large part of the ML community. Bayesian inference oers a number of attractive advantages over conventional approach
exibility in constructing complex models from simple parts;

A. Doucet (MLSS Sept. 2012)

Sept. 2012

4 / 136

Bayesian Inference and Machine Learning
Bayesian approaches have been adopted by a large part of the ML community. Bayesian inference oers a number of attractive advantages over conventional approach
exibility in constructing complex models from simple parts; the incorporation of prior knowledge is very natural;

A. Doucet (MLSS Sept. 2012)

Sept. 2012

4 / 136

Bayesian Inference and Machine Learning
Bayesian approaches have been adopted by a large part of the ML community. Bayesian inference oers a number of attractive advantages over conventional approach
exibility in constructing complex models from simple parts; the incorporation of prior knowledge is very natural; all modelling assumptions are made explicit;

A. Doucet (MLSS Sept. 2012)

Sept. 2012

4 / 136

Bayesian Inference and Machine Learning
Bayesian approaches have been adopted by a large part of the ML community. Bayesian inference oers a number of attractive advantages over conventional approach
exibility in constructing complex models from simple parts; the incorporation of prior knowledge is very natural; all modelling assumptions are made explicit; uncertainties over model order;

A. Doucet (MLSS Sept. 2012)

Sept. 2012

4 / 136

Bayesian Inference and Machine Learning
Bayesian approaches have been adopted by a large part of the ML community. Bayesian inference oers a number of attractive advantages over conventional approach
exibility in constructing complex models from simple parts; the incorporation of prior knowledge is very natural; all modelling assumptions are made explicit; uncertainties over model order; model parameters and predictions are technically straightforward to compute;

A. Doucet (MLSS Sept. 2012)

Sept. 2012

4 / 136

Bayesian Inference and Machine Learning
Bayesian approaches have been adopted by a large part of the ML community. Bayesian inference oers a number of attractive advantages over conventional approach
exibility in constructing complex models from simple parts; the incorporation of prior knowledge is very natural; all modelling assumptions are made explicit; uncertainties over model order; model parameters and predictions are technically straightforward to compute;

The cost to pay is that approximate inference techniques are necessary to approximate the resulting posterior distributions for all but trivial models.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

4 / 136

Approximate Inference Methods

Gaussian/Laplace approximation, local linearization, Extended Kalman lters.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

5 / 136

Approximate Inference Methods

Gaussian/Laplace approximation, local linearization, Extended Kalman lters. Variational methods, density assumed lters.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

5 / 136

Approximate Inference Methods

Gaussian/Laplace approximation, local linearization, Extended Kalman lters. Variational methods, density assumed lters. Expectation-Propagation.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

5 / 136

Approximate Inference Methods

Gaussian/Laplace approximation, local linearization, Extended Kalman lters. Variational methods, density assumed lters. Expectation-Propagation. Markov chain Monte Carlo (MCMC) methods.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

5 / 136

Approximate Inference Methods

Gaussian/Laplace approximation, local linearization, Extended Kalman lters. Variational methods, density assumed lters. Expectation-Propagation. Markov chain Monte Carlo (MCMC) methods. Sequential Monte Carlo (SMC) methods.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

5 / 136

Monte Carlo Methods
Variational and EP methods are computationally cheap but perform functional approximations of the posteriors of interest.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

6 / 136

Monte Carlo Methods
Variational and EP methods are computationally cheap but perform functional approximations of the posteriors of interest. Both MCMC and SMC are asymptotically (as you increase computational eorts) bias-free but computationally expensive.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

6 / 136

Monte Carlo Methods
Variational and EP methods are computationally cheap but perform functional approximations of the posteriors of interest. Both MCMC and SMC are asymptotically (as you increase computational eorts) bias-free but computationally expensive. MCMC are the tools of choice in Bayesian computation for over 20 years whereas SMC have been widely used for 15 years in vision and robotics.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

6 / 136

Monte Carlo Methods
Variational and EP methods are computationally cheap but perform functional approximations of the posteriors of interest. Both MCMC and SMC are asymptotically (as you increase computational eorts) bias-free but computationally expensive. MCMC are the tools of choice in Bayesian computation for over 20 years whereas SMC have been widely used for 15 years in vision and robotics. The development of new methodology combined to the emergence of cheap multicore architectures makes now SMC a powerful alternative/complementary approach to MCMC to address general Bayesian computational problems.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

6 / 136

Monte Carlo Methods
Variational and EP methods are computationally cheap but perform functional approximations of the posteriors of interest. Both MCMC and SMC are asymptotically (as you increase computational eorts) bias-free but computationally expensive. MCMC are the tools of choice in Bayesian computation for over 20 years whereas SMC have been widely used for 15 years in vision and robotics. The development of new methodology combined to the emergence of cheap multicore architectures makes now SMC a powerful alternative/complementary approach to MCMC to address general Bayesian computational problems. The aim of these lectures is to provide an introduction to this active research eld and discuss some open research problems.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

6 / 136

Some References and Resources

A.D., J.F.G. De Freitas & N.J. Gordon (editors), Sequential Monte Carlo Methods in Practice, Springer-Verlag: New York, 2001.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

7 / 136

Some References and Resources

A.D., J.F.G. De Freitas & N.J. Gordon (editors), Sequential Monte Carlo Methods in Practice, Springer-Verlag: New York, 2001. P. Del Moral, Feynman-Kac Formulae: Genealogical and Interacting Particle Systems with Applications, Springer-Verlag: New York, 2004.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

7 / 136

Some References and Resources

A.D., J.F.G. De Freitas & N.J. Gordon (editors), Sequential Monte Carlo Methods in Practice, Springer-Verlag: New York, 2001. P. Del Moral, Feynman-Kac Formulae: Genealogical and Interacting Particle Systems with Applications, Springer-Verlag: New York, 2004. O. Capp, E. Moulines & T. Ryden, Hidden Markov Models, Springer-Verlag: New York, 2005.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

7 / 136

Some References and Resources

A.D., J.F.G. De Freitas & N.J. Gordon (editors), Sequential Monte Carlo Methods in Practice, Springer-Verlag: New York, 2001. P. Del Moral, Feynman-Kac Formulae: Genealogical and Interacting Particle Systems with Applications, Springer-Verlag: New York, 2004. O. Capp, E. Moulines & T. Ryden, Hidden Markov Models, Springer-Verlag: New York, 2005. Webpage with links to papers and codes: http://www.stats.ox.ac.uk/~doucet/smc_resources.html

A. Doucet (MLSS Sept. 2012)

Sept. 2012

7 / 136

Some References and Resources

A.D., J.F.G. De Freitas & N.J. Gordon (editors), Sequential Monte Carlo Methods in Practice, Springer-Verlag: New York, 2001. P. Del Moral, Feynman-Kac Formulae: Genealogical and Interacting Particle Systems with Applications, Springer-Verlag: New York, 2004. O. Capp, E. Moulines & T. Ryden, Hidden Markov Models, Springer-Verlag: New York, 2005. Webpage with links to papers and codes: http://www.stats.ox.ac.uk/~doucet/smc_resources.html Thousands of papers on the subject appear every year.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

7 / 136

Organization of Lectures

State-Space Models (approx.4 hours)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

8 / 136

Organization of Lectures

State-Space Models (approx.4 hours)
SMC ltering and smoothing

A. Doucet (MLSS Sept. 2012)

Sept. 2012

8 / 136

Organization of Lectures

State-Space Models (approx.4 hours)
SMC ltering and smoothing Maximum likelihood parameter inference

A. Doucet (MLSS Sept. 2012)

Sept. 2012

8 / 136

Organization of Lectures

State-Space Models (approx.4 hours)
SMC ltering and smoothing Maximum likelihood parameter inference Bayesian parameter inference

A. Doucet (MLSS Sept. 2012)

Sept. 2012

8 / 136

Organization of Lectures

State-Space Models (approx.4 hours)
SMC ltering and smoothing Maximum likelihood parameter inference Bayesian parameter inference

Beyond State-Space Models (approx. 2 hours)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

8 / 136

Organization of Lectures

State-Space Models (approx.4 hours)
SMC ltering and smoothing Maximum likelihood parameter inference Bayesian parameter inference

Beyond State-Space Models (approx. 2 hours)
SMC methods for generic sequence of target distributions

A. Doucet (MLSS Sept. 2012)

Sept. 2012

8 / 136

Organization of Lectures

State-Space Models (approx.4 hours)
SMC ltering and smoothing Maximum likelihood parameter inference Bayesian parameter inference

Beyond State-Space Models (approx. 2 hours)
SMC methods for generic sequence of target distributions SMC samplers.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

8 / 136

Organization of Lectures

State-Space Models (approx.4 hours)
SMC ltering and smoothing Maximum likelihood parameter inference Bayesian parameter inference

Beyond State-Space Models (approx. 2 hours)
SMC methods for generic sequence of target distributions SMC samplers. Approximate Bayesian Computation.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

8 / 136

Organization of Lectures

State-Space Models (approx.4 hours)
SMC ltering and smoothing Maximum likelihood parameter inference Bayesian parameter inference

Beyond State-Space Models (approx. 2 hours)
SMC methods for generic sequence of target distributions SMC samplers. Approximate Bayesian Computation. Optimal design, optimal control.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

8 / 136

State-Space Models
Let fXt gt
1

be a latent/hidden X -valued Markov process with X1 ( ) and Xt j (Xt
1

= x)

f ( j x) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

9 / 136

State-Space Models
Let fXt gt
1

be a latent/hidden X -valued Markov process with X1 ( ) and Xt j (Xt
1

= x)

f ( j x) .

Let fYt gt 1 be an Y -valued Markov observation process such that observations are conditionally independent given fXt gt 1 and Yt j ( Xt = x ) g ( j x) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

9 / 136

State-Space Models
Let fXt gt
1

be a latent/hidden X -valued Markov process with X1 ( ) and Xt j (Xt
1

= x)

f ( j x) .

Let fYt gt 1 be an Y -valued Markov observation process such that observations are conditionally independent given fXt gt 1 and Yt j ( Xt = x ) g ( j x) .

General class of time series models aka Hidden Markov Models (HMM) including Xt = ( Xt
1 , Vt ) ,

Yt = ( Xt , W t )

where Vt , Wt are two sequences of i.i.d. random variables.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

9 / 136

State-Space Models
Let fXt gt
1

be a latent/hidden X -valued Markov process with X1 ( ) and Xt j (Xt
1

= x)

f ( j x) .

Let fYt gt 1 be an Y -valued Markov observation process such that observations are conditionally independent given fXt gt 1 and Yt j ( Xt = x ) g ( j x) .

General class of time series models aka Hidden Markov Models (HMM) including Xt = ( Xt
1 , Vt ) ,

Yt = ( Xt , W t )

where Vt , Wt are two sequences of i.i.d. random variables. Aim: Infer fXt g given observations fYt g on-line or o-line.
A. Doucet (MLSS Sept. 2012) Sept. 2012 9 / 136

State-Space Models
State-space models are ubiquitous in control, data mining, econometrics, geosciences, system biology etc. Since Jan. 2012, more than 13,500 papers have already appeared (source: Google Scholar).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

10 / 136

State-Space Models
State-space models are ubiquitous in control, data mining, econometrics, geosciences, system biology etc. Since Jan. 2012, more than 13,500 papers have already appeared (source: Google Scholar). Finite State-space HMM: X is a nite space, i.e. fXt g is a nite Markov chain Yt j ( Xt = x ) g ( j x )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

10 / 136

State-Space Models
State-space models are ubiquitous in control, data mining, econometrics, geosciences, system biology etc. Since Jan. 2012, more than 13,500 papers have already appeared (source: Google Scholar). Finite State-space HMM: X is a nite space, i.e. fXt g is a nite Markov chain Yt j ( Xt = x ) g ( j x ) Linear Gaussian state-space model Xt Yt

= AXt

1

+ BVt , Vt

i.i.d.

= CXt + DWt , Wt

i.i.d.

N (0, I )

N (0, I )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

10 / 136

State-Space Models
State-space models are ubiquitous in control, data mining, econometrics, geosciences, system biology etc. Since Jan. 2012, more than 13,500 papers have already appeared (source: Google Scholar). Finite State-space HMM: X is a nite space, i.e. fXt g is a nite Markov chain Yt j ( Xt = x ) g ( j x ) Linear Gaussian state-space model Xt Yt

= AXt

1

+ BVt , Vt

i.i.d.

= CXt + DWt , Wt

i.i.d.

N (0, I )

Switching Linear Gaussian state-space model: Xt = Xt1 , Xt2 where Xt1 is a nite Markov chain, Xt2 = A Xt1 Xt2 Yt
1

N (0, I )

+ B Xt1 Vt , Vt

i.i.d.

= C Xt1 Xt2 + D Xt1 Wt , Wt

i.i.d.

N (0, I )
Sept. 2012 10 / 136

N (0, I )

A. Doucet (MLSS Sept. 2012)

State-Space Models
Stochastic Volatility model Xt Yt
i.i.d.

= Xt

1

+ Vt , Vt

= exp (Xt /2) Wt , Wt

i.i.d.

N (0, 1) N (0, 1)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

11 / 136

State-Space Models
Stochastic Volatility model Xt Yt
i.i.d.

= Xt

1

+ Vt , Vt

= exp (Xt /2) Wt , Wt

i.i.d.

N (0, 1) N (0, 1)

Biochemical Network model Pr Xt1+dt =xt1+1, Xt2+dt =xt2 xt1 , xt2 = xt1 dt + o (dt ) , Pr Xt1+dt =xt1 1, Xt2+dt =xt2+1 xt1 , xt2 = xt1 xt2 dt + o (dt ) , Pr Xt1+dt =xt1 , Xt2+dt =xt2 1 xt1 , xt2 = xt2 dt + o (dt ) , with
1 Yk = Xk T + Wk with Wk i.i.d.

N 0, 2 .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

11 / 136

State-Space Models
Stochastic Volatility model Xt Yt
i.i.d.

= Xt

1

+ Vt , Vt

= exp (Xt /2) Wt , Wt

i.i.d.

N (0, 1) N (0, 1)

Biochemical Network model Pr Xt1+dt =xt1+1, Xt2+dt =xt2 xt1 , xt2 = xt1 dt + o (dt ) , Pr Xt1+dt =xt1 1, Xt2+dt =xt2+1 xt1 , xt2 = xt1 xt2 dt + o (dt ) , Pr Xt1+dt =xt1 , Xt2+dt =xt2 1 xt1 , xt2 = xt2 dt + o (dt ) , with
1 Yk = Xk T + Wk with Wk i.i.d.

Nonlinear Diusion model dXt Yk
i.i.d.

N 0, 2 .

= (Xt ) dt + (Xt ) dVt , Vt Brownian motion = (Xk T ) +Wk , Wk N 0, 2 .
Sept. 2012 11 / 136

A. Doucet (MLSS Sept. 2012)

Inference in State-Space Models
Given observations y1:t := (y1 , y2 , . . . , yt ), inference about X1:t := (X1 , ..., Xt ) relies on the posterior p ( x1:t j y1:t ) = where p (x1:t , y1:t ) = (x1 ) f ( xk j xk p (y1:t ) =
Z
t 1) k =2

p (x1:t , y1:t ) p (y1:t )

|

Z

p (x1:t )

p (x1:t , y1:t ) dx1:t

{z

}k =1 {z |

g ( yk j xk ),
p ( y1:t jx1:t )

t

}

A. Doucet (MLSS Sept. 2012)

Sept. 2012

12 / 136

Inference in State-Space Models
Given observations y1:t := (y1 , y2 , . . . , yt ), inference about X1:t := (X1 , ..., Xt ) relies on the posterior p ( x1:t j y1:t ) = where p (x1:t , y1:t ) = (x1 ) f ( xk j xk p (y1:t ) =
Z
t 1) k =2

p (x1:t , y1:t ) p (y1:t )

|

When X is nite & linear Gaussian models, fp ( xt j y1:t )gt 1 can be computed exactly. For non-linear models, approximations are required: EKF, UKF, Gaussian sum lters, etc.

Z

p (x1:t )

p (x1:t , y1:t ) dx1:t

{z

}k =1 {z |

g ( yk j xk ),
p ( y1:t jx1:t )

t

}

A. Doucet (MLSS Sept. 2012)

Sept. 2012

12 / 136

Inference in State-Space Models
Given observations y1:t := (y1 , y2 , . . . , yt ), inference about X1:t := (X1 , ..., Xt ) relies on the posterior p ( x1:t j y1:t ) = where p (x1:t , y1:t ) = (x1 ) f ( xk j xk p (y1:t ) =
Z
t 1) k =2

p (x1:t , y1:t ) p (y1:t )

|

A. Doucet (MLSS Sept. 2012)

When X is nite & linear Gaussian models, fp ( xt j y1:t )gt 1 can be computed exactly. For non-linear models, approximations are required: EKF, UKF, Gaussian sum lters, etc. Approximations of fp ( xt j y1:t )gT=1 provide approximation of t p ( x1:T j y1:T ) .
Sept. 2012

Z

p (x1:t )

p (x1:t , y1:t ) dx1:t

{z

}k =1 {z |

g ( yk j xk ),
p ( y1:t jx1:t )

t

}

12 / 136

Monte Carlo Methods Basics
Assume you can generate X1:t MC approximation is
(i )

p ( x1:t j y1:t ) where i = 1, ..., N then 1 N

p ( x1:t j y1:t ) = b

i =1

X ( ) (x1:t )
i 1:t

N

A. Doucet (MLSS Sept. 2012)

Sept. 2012

13 / 136

Monte Carlo Methods Basics
Assume you can generate X1:t MC approximation is
(i )

p ( x1:t j y1:t ) where i = 1, ..., N then 1 N

Integration is straightforward. R t (x1:t ) p ( x1:t j y1:t ) dx1:t

p ( x1:t j y1:t ) = b

i =1

X ( ) (x1:t )
i 1:t

N

=

R

1 N

b t (x1:t ) p ( x1:t j y1:t ) dx1:t N 1 X1:t i=
(i )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

13 / 136

Monte Carlo Methods Basics
Assume you can generate X1:t MC approximation is
(i )

p ( x1:t j y1:t ) where i = 1, ..., N then 1 N

Integration is straightforward. R t (x1:t ) p ( x1:t j y1:t ) dx1:t
Z

p ( x1:t j y1:t ) = b

i =1

X ( ) (x1:t )
i 1:t

N

=

R

1 N

Marginalization is straightforward. p ( xk j y1:t ) = b p ( x1:t j y1:t ) dx1:k b

b t (x1:t ) p ( x1:t j y1:t ) dx1:t N 1 X1:t i=
(i )

1 dxk +1:t =

1 N

i =1

X ( ) (xk ) .
i k

N

A. Doucet (MLSS Sept. 2012)

Sept. 2012

13 / 136

Monte Carlo Methods Basics
Assume you can generate X1:t MC approximation is
(i )

p ( x1:t j y1:t ) where i = 1, ..., N then 1 N

Integration is straightforward. R t (x1:t ) p ( x1:t j y1:t ) dx1:t
Z

p ( x1:t j y1:t ) = b

i =1

X ( ) (x1:t )
i 1:t

N

=

R

1 N

Marginalization is straightforward. p ( xk j y1:t ) = b p ( x1:t j y1:t ) dx1:k b h
1 N

b t (x1:t ) p ( x1:t j y1:t ) dx1:t N 1 X1:t i=
(i )

1 dxk +1:t =

1 N

Basic and key property: V
A. Doucet (MLSS Sept. 2012)

i (i ) = C (t dim (X )) , i.e. N 1 X1:t i= N rate of convergence to zero is independent of dim (X ) and t.
Sept. 2012 13 / 136

i =1

X ( ) (xk ) .
i k

N

Monte Carlo Methods
Problem 1: We cannot typically generate exact samples from p ( x1:t j y1:t ) for non-linear non-Gaussian models.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

14 / 136

Monte Carlo Methods
Problem 1: We cannot typically generate exact samples from p ( x1:t j y1:t ) for non-linear non-Gaussian models.

Problem 2: Even if we could, algorithms to generate samples from p ( x1:t j y1:t ) will have at least complexity O (t ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

14 / 136

Monte Carlo Methods
Problem 1: We cannot typically generate exact samples from p ( x1:t j y1:t ) for non-linear non-Gaussian models.

Problem 2: Even if we could, algorithms to generate samples from p ( x1:t j y1:t ) will have at least complexity O (t ) . Typical solution to problem 1 is to generate approximate samples using MCMC methods but these methods are not recursive.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

14 / 136

Monte Carlo Methods
Problem 1: We cannot typically generate exact samples from p ( x1:t j y1:t ) for non-linear non-Gaussian models.

Problem 2: Even if we could, algorithms to generate samples from p ( x1:t j y1:t ) will have at least complexity O (t ) . Typical solution to problem 1 is to generate approximate samples using MCMC methods but these methods are not recursive.

SMC Methods solves partially Problem 1 and Problem 2 by breaking the problem of sampling from p ( x1:t j y1:t ) into a collection of simpler subproblems. First approximate p ( x1 j y1 ) and p (y1 ) at time 1, then p ( x1:2 j y1:2 ) and p (y1:2 ) at time 2 and so on.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

14 / 136

Monte Carlo Methods
Problem 1: We cannot typically generate exact samples from p ( x1:t j y1:t ) for non-linear non-Gaussian models.

Problem 2: Even if we could, algorithms to generate samples from p ( x1:t j y1:t ) will have at least complexity O (t ) . Typical solution to problem 1 is to generate approximate samples using MCMC methods but these methods are not recursive.

SMC Methods solves partially Problem 1 and Problem 2 by breaking the problem of sampling from p ( x1:t j y1:t ) into a collection of simpler subproblems. First approximate p ( x1 j y1 ) and p (y1 ) at time 1, then p ( x1:2 j y1:2 ) and p (y1:2 ) at time 2 and so on. Each target distribution is approximated by a cloud of random samples termed particles evolving according to importance sampling and resampling steps.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

14 / 136

Standard Bayesian Recursion
In most textbooks, you will nd the following recursion for fp ( xt j y1:t )gt 1 .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

15 / 136

Standard Bayesian Recursion
In most textbooks, you will nd the following recursion for fp ( xt j y1:t )gt 1 . Prediction step p ( xt j y1:t
1)

= = =

Z

p ( xt

Z Z

1 , xt j y1:t 1 ) dxt 1 1 , xt 1 ) p ( xt 1 j y1:t 1 ) dxt 1 1 ) p ( xt 1 j y1:t 1 ) dxt 1 .

p ( xt j y1:t f ( xt j xt

A. Doucet (MLSS Sept. 2012)

Sept. 2012

15 / 136

Standard Bayesian Recursion
In most textbooks, you will nd the following recursion for fp ( xt j y1:t )gt 1 . Prediction step p ( xt j y1:t
1)

= = =

Z

p ( xt

Z Z

1 , xt j y1:t 1 ) dxt 1 1 , xt 1 ) p ( xt 1 j y1:t 1 ) dxt 1 1 ) p ( xt 1 j y1:t 1 ) dxt 1 .

p ( xt j y1:t f ( xt j xt

Bayes Updating step

p ( xt j y1:t ) = where p ( yt j y1:t
A. Doucet (MLSS Sept. 2012)

1)

=

Z

g ( yt j xt ) p ( xt j y1:t p ( yt j y1:t 1 ) g ( yt j xt ) p ( xt j y1:t

1)

1 ) dxt

Sept. 2012

15 / 136

Standard Bayesian Recursion
In most textbooks, you will nd the following recursion for fp ( xt j y1:t )gt 1 . Prediction step p ( xt j y1:t
1)

= = =

Z

p ( xt

Z Z

1 , xt j y1:t 1 ) dxt 1 1 , xt 1 ) p ( xt 1 j y1:t 1 ) dxt 1 1 ) p ( xt 1 j y1:t 1 ) dxt 1 .

p ( xt j y1:t f ( xt j xt

Bayes Updating step

p ( xt j y1:t ) = where p ( yt j y1:t
A. Doucet (MLSS Sept. 2012)

1)

=

This is the recursion implemented by Wonham and Kalman lters...
Sept. 2012 15 / 136

Z

g ( yt j xt ) p ( xt j y1:t p ( yt j y1:t 1 ) g ( yt j xt ) p ( xt j y1:t

1)

1 ) dxt

Bayesian Recursion on Path Space
SMC approximate directly fp ( x1:t j y1:t )gt 1 not fp ( xt j y1:t )gt 1 and relies on p (x1:t , y1:t ) g ( yt j xt ) f ( xt j xt 1 ) p (x1:t 1 , y1:t 1 ) p ( x1:t j y1:t ) = = p (y1:t ) p ( yt j y1:t 1 ) p (y1:t 1 )

=
where

}| z g ( yt j xt ) f ( xt j xt 1 ) p ( x1:t p ( yt j y1:t 1 )
1)

predictive p ( x1:t jy1:t

1)

1 j y1:t

{ 1)
1 ) dx1:t

p ( yt j y1:t

=

Z

g ( yt j xt ) p ( x1:t j y1:t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

16 / 136

Bayesian Recursion on Path Space
SMC approximate directly fp ( x1:t j y1:t )gt 1 not fp ( xt j y1:t )gt 1 and relies on p (x1:t , y1:t ) g ( yt j xt ) f ( xt j xt 1 ) p (x1:t 1 , y1:t 1 ) p ( x1:t j y1:t ) = = p (y1:t ) p ( yt j y1:t 1 ) p (y1:t 1 )

=
where

}| z g ( yt j xt ) f ( xt j xt 1 ) p ( x1:t p ( yt j y1:t 1 )
1)

predictive p ( x1:t jy1:t

1)

1 j y1:t

{ 1)
1 ) dx1:t

p ( yt j y1:t Prediction Update

=

This can be alternatively written as p ( x1:t j y1:t 1 ) = f ( xt j xt 1 ) p ( x1:t g ( yt jxt )p ( x1:t jy1:t 1 ) . p ( x1:t j y1:t ) = p ( yt jy1:t 1 )
1 j y1:t 1 ) ,

Z

g ( yt j xt ) p ( x1:t j y1:t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

16 / 136

Bayesian Recursion on Path Space
SMC approximate directly fp ( x1:t j y1:t )gt 1 not fp ( xt j y1:t )gt 1 and relies on p (x1:t , y1:t ) g ( yt j xt ) f ( xt j xt 1 ) p (x1:t 1 , y1:t 1 ) p ( x1:t j y1:t ) = = p (y1:t ) p ( yt j y1:t 1 ) p (y1:t 1 )

=
where

}| z g ( yt j xt ) f ( xt j xt 1 ) p ( x1:t p ( yt j y1:t 1 )
1)

predictive p ( x1:t jy1:t

1)

1 j y1:t

{ 1)
1 ) dx1:t

p ( yt j y1:t Prediction Update

=

This can be alternatively written as p ( x1:t j y1:t 1 ) = f ( xt j xt 1 ) p ( x1:t g ( yt jxt )p ( x1:t jy1:t 1 ) . p ( x1:t j y1:t ) = p ( yt jy1:t 1 )
1 j y1:t 1 ) ,

Z

g ( yt j xt ) p ( x1:t j y1:t

SMC is a simple and natural simulation-based implementation of this recursion.
A. Doucet (MLSS Sept. 2012) Sept. 2012 16 / 136

Monte Carlo Implementation of Prediction Step

Assume you have at time t p ( x1:t b

1

1 j y1:t 1 )

=

1 N

i =1

X ( )

N

i 1:t 1

(x1:t

1) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

17 / 136

Monte Carlo Implementation of Prediction Step

Assume you have at time t p ( x1:t b

1

1 j y1:t 1 )

=

1 N

i =1

X ( )

N

i 1:t 1

(x1:t

1) .

e (i ) By sampling Xt then

f

xt j Xt

(i ) 1

p ( x1:t j y1:t b

1)

=

(i ) e (i ) e (i ) and setting X1:t = X1:t 1 , Xt

1 N

i =1

X ( ) (x1:t ) . e
i 1:t

N

A. Doucet (MLSS Sept. 2012)

Sept. 2012

17 / 136

Monte Carlo Implementation of Prediction Step

Assume you have at time t p ( x1:t b

1

1 j y1:t 1 )

=

1 N

i =1

X ( )

N

i 1:t 1

(x1:t

1) .

e (i ) By sampling Xt then

f

xt j Xt

(i ) 1

Sampling from f ( xt j xt 1 ) is usually straightforward and can be done even if f ( xt j xt 1 ) does not admit any analytical expression; e.g. biochemical network models.

p ( x1:t j y1:t b

1)

=

(i ) e (i ) e (i ) and setting X1:t = X1:t 1 , Xt

1 N

i =1

X ( ) (x1:t ) . e
i 1:t

N

A. Doucet (MLSS Sept. 2012)

Sept. 2012

17 / 136

Importance Sampling Implementation of Updating Step
Our target at time t is p ( x1:t j y1:t ) = so by substituting p ( x1:t j y1:t b p ( yt j y1:t b
1)

g ( yt j xt ) p ( x1:t j y1:t p ( yt j y1:t 1 )
1)

1)

= =

Z

to p ( x1:t j y1:t

1)

we obtain
1 ) dx1:t

1 N

g ( yt j xt ) p ( x1:t j y1:t b
i =1

g

N

e (i ) . yt j Xt

A. Doucet (MLSS Sept. 2012)

Sept. 2012

18 / 136

Importance Sampling Implementation of Updating Step
Our target at time t is p ( x1:t j y1:t ) = so by substituting p ( x1:t j y1:t b p ( yt j y1:t b
1)

g ( yt j xt ) p ( x1:t j y1:t p ( yt j y1:t 1 )
1)

1)

= =

Z

to p ( x1:t j y1:t

1)

we obtain
1 ) dx1:t

1 N

g ( yt j xt ) p ( x1:t j y1:t b
i =1

g

N

We now have p ( x1:t j y1:t ) = e
(i )

e (i ) . yt j Xt
1)

with Wt

g

A. Doucet (MLSS Sept. 2012)

e (i ) , N 1 Wt(i ) = 1. yt j Xt i=

g ( yt j xt ) p ( x1:t j y1:t b p ( yt j y1:t 1 ) b

=

i =1

Wt

N

(i )

X (i ) (x1:t ) . e
1:t Sept. 2012 18 / 136

Multinomial Resampling
We have a weighted approximation p ( x1:t j y1:t ) of p ( x1:t j y1:t ) e p ( x1:t j y1:t ) = e
i =1 N

Wt

(i )

X (i ) (x1:t ) . e
1:t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

19 / 136

Multinomial Resampling
We have a weighted approximation p ( x1:t j y1:t ) of p ( x1:t j y1:t ) e To obtain N samples X1:t approximately distributed according to p ( x1:t j y1:t ), resample N times with replacement X1:t to obtain
(i )
N

p ( x1:t j y1:t ) = e
(i )

i =1

Wt

(i )

X (i ) (x1:t ) . e
1:t

N 1 N Nt p ( x1:t j y1:t ) = b (i X1:t) (x1:t ) = N X1:t) (x1:t ) e (i N i =1 i =1 n o h i (i ) (i ) (i ) where Nt follow a multinomial with E Nt = NWt , h i (1 ) (i ) (i ) V Nt = NWt 1 Wt .
A. Doucet (MLSS Sept. 2012) Sept. 2012 19 / 136

p ( x1:t j y1:t ) e

(i )

Multinomial Resampling
We have a weighted approximation p ( x1:t j y1:t ) of p ( x1:t j y1:t ) e To obtain N samples X1:t approximately distributed according to p ( x1:t j y1:t ), resample N times with replacement X1:t to obtain
(i )
N

p ( x1:t j y1:t ) = e
(i )

i =1

Wt

(i )

X (i ) (x1:t ) . e
1:t

This can be achieved in O (N ).
A. Doucet (MLSS Sept. 2012)

N 1 N Nt p ( x1:t j y1:t ) = b (i X1:t) (x1:t ) = N X1:t) (x1:t ) e (i N i =1 i =1 n o h i (i ) (i ) (i ) where Nt follow a multinomial with E Nt = NWt , h i (1 ) (i ) (i ) V Nt = NWt 1 Wt .
Sept. 2012 19 / 136

p ( x1:t j y1:t ) e

(i )

Vanilla SMC: Bootstrap Filter (Gordon et al., 1993)
At time t = 1 e (i ) Sample X1 (x1 ) then

p ( x1 j y1 ) = e

i =1

W1

N

(i )

X (i ) (x1 ) , W1 e
1

(i )

g

e (i ) y1 j X1 .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

20 / 136

Vanilla SMC: Bootstrap Filter (Gordon et al., 1993)
At time t = 1 e (i ) Sample X1 (x1 ) then

Resample X1

p ( x1 j y1 ) = e
(i )

i =1

W1

N

(i )

p ( x1 j y1 ) to obtain p ( x1 j y1 ) = e b

X (i ) (x1 ) , W1 e
1

(i )

g

1 N

e (i ) y1 j X1 .
1

N 1 X (i ) (x1 ). i=

A. Doucet (MLSS Sept. 2012)

Sept. 2012

20 / 136

Vanilla SMC: Bootstrap Filter (Gordon et al., 1993)
At time t = 1 e (i ) Sample X1 (x1 ) then

Resample X1

p ( x1 j y1 ) = e
(i )

i =1

W1

N

(i )

p ( x1 j y1 ) to obtain p ( x1 j y1 ) = e b

X (i ) (x1 ) , W1 e
1

(i )

g

1 N

e (i ) y1 j X1 .
1

N 1 X (i ) (x1 ). i=

A. Doucet (MLSS Sept. 2012)

Sept. 2012

20 / 136

Vanilla SMC: Bootstrap Filter (Gordon et al., 1993)
At time t = 1 e (i ) Sample X1 (x1 ) then

Resample X1 At time t 2 e (i ) Sample Xt

p ( x1 j y1 ) = e
(i )

i =1

W1

N

(i )

p ( x1 j y1 ) to obtain p ( x1 j y1 ) = e b xt j Xt
N

X (i ) (x1 ) , W1 e
1

(i )

g

1 N

e (i ) y1 j X1 .
1

N 1 X (i ) (x1 ). i= and

f

(i ) 1

p ( x1:t j y1:t ) = e

i =1

Wt

(i )

(i ) e (i ) e (i ) , set X1:t = X1:t 1 , Xt

X (i ) (x1:t ) , Wt e
1:t

(i )

g

e (i ) . yt j Xt

A. Doucet (MLSS Sept. 2012)

Sept. 2012

20 / 136

Vanilla SMC: Bootstrap Filter (Gordon et al., 1993)
At time t = 1 e (i ) Sample X1 (x1 ) then

Resample X1 At time t 2 e (i ) Sample Xt

p ( x1 j y1 ) = e
(i )

i =1

W1

N

(i )

p ( x1 j y1 ) to obtain p ( x1 j y1 ) = e b xt j Xt
N

X (i ) (x1 ) , W1 e
1

(i )

g

1 N

e (i ) y1 j X1 .
1

N 1 X (i ) (x1 ). i= and

f

(i ) 1

A. Doucet (MLSS Sept. 2012)

Resample X1:t p ( x1:t j y1:t ) = b

p ( x1:t j y1:t ) = e
(i )
1 N

i =1

Wt

(i )

(i ) e (i ) e (i ) , set X1:t = X1:t 1 , Xt

p ( x1:t j y1:t ) to obtain e N 1 X (i ) (x1:t ). i=
1:t

X (i ) (x1:t ) , Wt e
1:t

(i )

g

e (i ) . yt j Xt

Sept. 2012

20 / 136

SMC Output
At time t, we get p ( x1:t j y1:t ) = e
N

i =1

Wt
1 N
N i =1

(i )

p ( x1:t j y1:t ) = b

X ( ) (x1:t ) .
i 1:t

X (i ) (x1:t ) , e
1:t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

21 / 136

SMC Output
At time t, we get p ( x1:t j y1:t ) = e
N

i =1

Wt
1 N
N i =1

(i )

The marginal likelihood estimate is given by p (y1:t ) = b b p ( yk j y1:k
t 1)

p ( x1:t j y1:t ) = b

X ( ) (x1:t ) .
i 1:t

X (i ) (x1:t ) , e
1:t

=

k =1

k =1

t

1 N

i =1

g

N

e (i ) yk j Xk

!

.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

21 / 136

SMC Output
At time t, we get p ( x1:t j y1:t ) = e
N

i =1

Wt
1 N
N i =1

(i )

The marginal likelihood estimate is given by p (y1:t ) = b b p ( yk j y1:k
t 1)

p ( x1:t j y1:t ) = b

X ( ) (x1:t ) .
i 1:t

X (i ) (x1:t ) , e
1:t

=

k =1

k =1

t

1 N

i =1

g

N

Computational complexity is O (N ) at each time step and memory requirements O (tN ) .

e (i ) yk j Xk

!

.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

21 / 136

SMC Output
At time t, we get p ( x1:t j y1:t ) = e
N

i =1

Wt
1 N
N i =1

(i )

The marginal likelihood estimate is given by p (y1:t ) = b b p ( yk j y1:k
t 1)

p ( x1:t j y1:t ) = b

X ( ) (x1:t ) .
i 1:t

X (i ) (x1:t ) , e
1:t

=

k =1

k =1

t

1 N

i =1

g

N

Computational complexity is O (N ) at each time step and memory requirements O (tN ) . If we are only interested in p ( xt j y1:t ) or p ( st (x1:t )j y1:t ) where 2 st (x1:t ) = t (xt , st 1 (x1:t 1 )) - e.g. st (x1:t ) = t =1 xk - is k xed-dimensional then memory requirements O (N ) .
A. Doucet (MLSS Sept. 2012) Sept. 2012 21 / 136

e (i ) yk j Xk

!

.

SMC on Path-Space - gures by Olivier Capp e
1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

b Figure: p ( x1 j y1 ) and E [ X1 j y1 ] (top) and particle approximation of p ( x1 j y1 ) (bottom) (MLSS Sept. 2012) A. Doucet Sept. 2012 22 / 136

1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

b b Figure: p ( x1 j y1 ) , p ( x2 j y1 :2 )and E [ X1 j y1 ] , E [ X2 j y1 :2 ] (top) and particle approximation of p ( x1 :2 j y1 :2 ) (bottom)
A. Doucet (MLSS Sept. 2012) Sept. 2012 23 / 136

1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

b Figure: p ( xt j y1 :t ) and E [ Xt j y1 :t ] for t = 1, 2, 3 (top) and particle approximation of p ( x1 :3 j y1 :3 ) (bottom)
A. Doucet (MLSS Sept. 2012) Sept. 2012 24 / 136

1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

b Figure: p ( xt j y1 :t ) and E [ Xt j y1 :t ] for t = 1, ..., 10 (top) and particle approximation of p ( x1 :10 j y1 :10 ) (bottom)
A. Doucet (MLSS Sept. 2012) Sept. 2012 25 / 136

1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

1.6 1.4 1.2
state

1 0.8 0.6 0.4

5

10 time index

15

20

25

b Figure: p ( xt j y1 :t ) and E [ Xt j y1 :t ] for t = 1, ..., 24 (top) and particle approximation of p ( x1 :24 j y1 :24 ) (bottom)
A. Doucet (MLSS Sept. 2012) Sept. 2012 26 / 136

Remarks
Empirically this SMC strategy performs well in terms of estimating the marginals fp ( xt j y1:t )gt 1 . This is what is only necessary in many applications thankfully.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

27 / 136

Remarks
Empirically this SMC strategy performs well in terms of estimating the marginals fp ( xt j y1:t )gt 1 . This is what is only necessary in many applications thankfully. However, the joint distribution p ( x1:t j y1:t ) is poorly estimated when t is large; i.e. we have in the previous example p ( x1:11 j y1:24 ) = X 1:11 (x1:11 ) . b

A. Doucet (MLSS Sept. 2012)

Sept. 2012

27 / 136

Remarks
Empirically this SMC strategy performs well in terms of estimating the marginals fp ( xt j y1:t )gt 1 . This is what is only necessary in many applications thankfully. However, the joint distribution p ( x1:t j y1:t ) is poorly estimated when t is large; i.e. we have in the previous example p ( x1:11 j y1:24 ) = X 1:11 (x1:11 ) . b p ( x1:k j y1:t ) = X 1:k (x1:k ) ; b

Degeneracy problem. For any N and any k, there exists t (k, N ) such that for any t t (k, N )

p ( x1:t j y1:t ) is an unreliable approximation of p ( x1:t j y1:t ) as t %. b
A. Doucet (MLSS Sept. 2012) Sept. 2012 27 / 136

Another Illustration of the Degeneracy Phenomenon
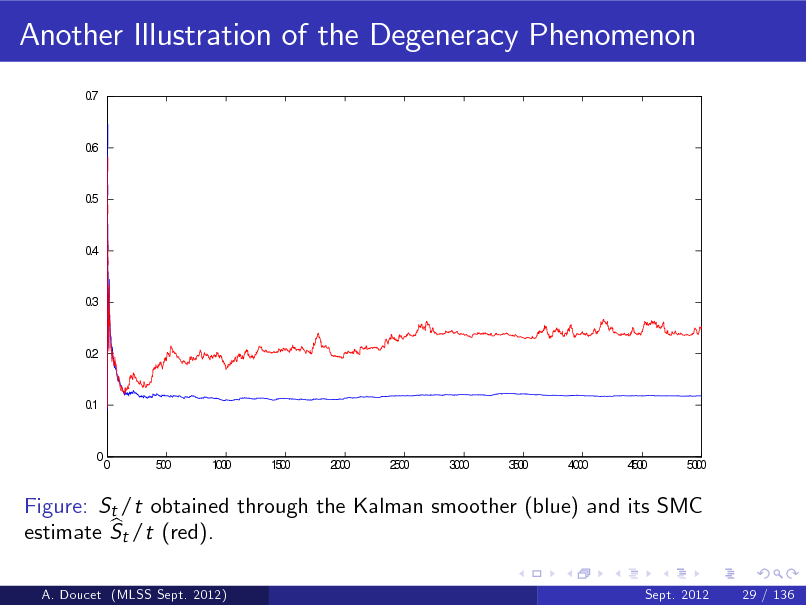
For the linear Gaussian state-space model described before, we can compute exactly St /t where ! Z St =
k =1

xk2

t

p ( x1:t j y1:t ) dx1:t

using Kalman techniques.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

28 / 136

Another Illustration of the Degeneracy Phenomenon
For the linear Gaussian state-space model described before, we can compute exactly St /t where ! Z St =
k =1

xk2

t

p ( x1:t j y1:t ) dx1:t

using Kalman techniques. b We compute the SMC estimate of this quantity using St /t where ! Z t 2 b St = b xk p ( x1:t j y1:t ) dx1:t
k =1

can be computed sequentially.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

28 / 136

Another Illustration of the Degeneracy Phenomenon
0 .7

0 .6

0 .5

0 .4

0 .3

0 .2

0 .1

0

0

5 00

10 00

10 50

20 00

20 50

30 00

30 50

40 00

40 50

50 00

Figure: St /t obtained through the Kalman smoother (blue) and its SMC b estimate St /t (red).
A. Doucet (MLSS Sept. 2012)

Sept. 2012

29 / 136

Some Convergence Results for SMC
Numerous convergence results for SMC are available; see (Del Moral, 2004).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

30 / 136

Some Convergence Results for SMC
Numerous convergence results for SMC are available; see (Del Moral, 2004). Let t : X t ! R and consider t = bt =
Z Z

t (x1:t ) p ( x1:t j y1:t ) dx1:t , b t (x1:t ) p ( x1:t j y1:t ) dx1:t = 1 N
i =1

t

N

X1:t .

(i )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

30 / 136

Some Convergence Results for SMC
Numerous convergence results for SMC are available; see (Del Moral, 2004). Let t : X t ! R and consider t = bt =
Z Z

t (x1:t ) p ( x1:t j y1:t ) dx1:t , b t (x1:t ) p ( x1:t j y1:t ) dx1:t = 1 N
i =1

t

N

X1:t . 1

(i )

We can prove that for any bounded function and any p B (t ) c (p ) k k 1/p p E [j b t t jp ] , N p lim N ( b t t ) ) N 0, 2 . t

N !

A. Doucet (MLSS Sept. 2012)

Sept. 2012

30 / 136

Some Convergence Results for SMC
Numerous convergence results for SMC are available; see (Del Moral, 2004). Let t : X t ! R and consider t = bt =
Z Z

t (x1:t ) p ( x1:t j y1:t ) dx1:t , b t (x1:t ) p ( x1:t j y1:t ) dx1:t = 1 N
i =1

t

N

X1:t . 1

(i )

We can prove that for any bounded function and any p B (t ) c (p ) k k 1/p p E [j b t t jp ] , N p lim N ( b t t ) ) N 0, 2 . t

N !

Very weak results: B (t ) and 2 can increase with t and will for a t path-dependent t (x1:t ) as the degeneracy problem suggests.
A. Doucet (MLSS Sept. 2012) Sept. 2012 30 / 136

Stronger Convergence Results
Assume the following exponentially stability assumption: For any 0 x1 , x1 p ( xt j y2:t , X1 = x1 )
0 p xt j y2:t , X1 = x1

1 2

Z

dxt

t for 0

< 1.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

31 / 136

Stronger Convergence Results
Assume the following exponentially stability assumption: For any 0 x1 , x1 p ( xt j y2:t , X1 = x1 )
0 p xt j y2:t , X1 = x1

1 2

Z

dxt

t for 0

< 1.

Marginal distribution. For t (x1:t ) = (xt L:t ), there exists B1 , B2 < s.t. B1 c ( p ) k k 1/p p E [j b t t jp ] , N p lim N ( b t t ) ) N 0, 2 where 2 B2 , t t i.e. there is no accumulation of numerical errors over time.
N !

A. Doucet (MLSS Sept. 2012)

Sept. 2012

31 / 136

Stronger Convergence Results
Assume the following exponentially stability assumption: For any 0 x1 , x1 p ( xt j y2:t , X1 = x1 )
0 p xt j y2:t , X1 = x1

1 2

Z

dxt

t for 0

< 1.

i.e. there is no accumulation of numerical errors over time. b L1 distance. If p ( x1:t j y1:t ) = E (p ( x1:t j y1:t )), there exists B3 < s.t. Z B3 t ; jp ( x1:t j y1:t ) p ( x1:t j y1:t )j dx1:t N i.e. the bias only increases in t.
A. Doucet (MLSS Sept. 2012) Sept. 2012 31 / 136

Marginal distribution. For t (x1:t ) = (xt L:t ), there exists B1 , B2 < s.t. B1 c ( p ) k k 1/p p E [j b t t jp ] , N p lim N ( b t t ) ) N 0, 2 where 2 B2 , t t
N !

Stronger Convergence Results
Unbiasedness. The marginal likelihood estimate is unbiased E (p (y1:t )) = p (y1:t ) . b

A. Doucet (MLSS Sept. 2012)

Sept. 2012

32 / 136

Stronger Convergence Results
Unbiasedness. The marginal likelihood estimate is unbiased E (p (y1:t )) = p (y1:t ) . b

Relative Variance Bound. There exists B4 < ! 2 p (y1:t ) b B4 t E 1 p (y1:t ) N

A. Doucet (MLSS Sept. 2012)

Sept. 2012

32 / 136

Stronger Convergence Results
Unbiasedness. The marginal likelihood estimate is unbiased E (p (y1:t )) = p (y1:t ) . b

Relative Variance Bound. There exists B4 < ! 2 p (y1:t ) b B4 t E 1 p (y1:t ) N

Central Limit Theorem. There exists B5 < s.t. p lim N (log p (y1:t ) log p (y1:t )) ) N 0, 2 with 2 b t t
N !

B5 t.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

32 / 136

Basic Idea Used to Establish Uniform Lp Bounds
We denote k (xk ) = p ( xk j y1:k and its particle approximation. bk (xk ) = p ( xk j y1:k b
1) 1)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

33 / 136

Basic Idea Used to Establish Uniform Lp Bounds
We denote k (xk ) = p ( xk j y1:k and its particle approximation. bk (xk ) = p ( xk j y1:k b t = k ,t ( k ) , which saties k ,t ( k ) (xt ) =
Z
1) 1)

Let k ,t be the measure-valued mapping such that

(x ) .p ( yk :t 1 j xk ) R k k p ( xt j xk , yk +1:t k (xk ) p ( yk :t 1 j xk ) dxk | {z }
p (xk jy1:t
1) Sept. 2012

1 ) dxk .

A. Doucet (MLSS Sept. 2012)

33 / 136

Key Decomposition Formula
1 + b1

! !

2 = 1,2 ( 1 ) 1,2 (b1 ) + b2

! ! ! + bt

! ! !
1

t = 1,t ( 1 ) 1,t (b1 )
1,t

!

Decomposition of the error bt t =

t + bt

2,t (b2 )

bt

1

k =1

t

k ,t (bk )

k ,t k

1,k

bk

1

A. Doucet (MLSS Sept. 2012)

Sept. 2012

34 / 136

Stability Properties
We have p ( xt j xk , yk +1:t where p ( xk +1:t j xk , yk +1:t
1) 1) =

Z

p ( xk +1:t j xk , yk +1:t
t

1 ) dxk +1:t 1

=

m =k +1

p ( xm j xm

1 , ym:t 1 )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

35 / 136

Stability Properties
We have p ( xt j xk , yk +1:t where p ( xk +1:t j xk , yk +1:t To summarize, we have k ,t ( k ) (xt ) =
Z
1) 1) =

Z

p ( xk +1:t j xk , yk +1:t
t

1 ) dxk +1:t 1

=

m =k +1

p ( xm j xm

1 , ym:t 1 )

(x ) .p ( yk :t 1 j xk ) R k k (xk ) p ( yk :t 1 j xk ) dxk | k {z }
m =k +1

t

p (xk jy1:t

1)

p ( xm j xm

1 , ym:t 1 ) dxk :t 1

A. Doucet (MLSS Sept. 2012)

Sept. 2012

35 / 136

Stability Properties
Assume there exists

> 0 s.t. for any x, x 0
1

x0

f x0 x

x0

and for any y , x, 0<g then there exists 0 1 2
Z

g (yj x)

g <

<1 k ,k +t 0 (x ) dx t

k ,k +t ( ) (x )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

36 / 136

Stability Properties
Assume there exists

> 0 s.t. for any x, x 0
1

x0

f x0 x

x0

and for any y , x, 0<g then there exists 0 1 2
Z

g (yj x)

g <

<1 k ,k +t 0 (x ) dx t

k ,k +t ( ) (x )

Hence we have k ,t ( k ) (xt ) as (t k ) ! .
Sept. 2012 36 / 136

0 k ,t k (xt )

A. Doucet (MLSS Sept. 2012)

Putting Everything Together
Under such strong mixing assumptions bt t = |k ,t (bk )
t

k =1

1 ' p t N

k ,t k {z
k +1

1,k

for 0 1

bk

1

}

A. Doucet (MLSS Sept. 2012)

Sept. 2012

37 / 136

Putting Everything Together
Under such strong mixing assumptions bt t = |k ,t (bk ) t jp ]
1/p t

k =1

1 ' p t N

We can then obtain results such as there exists B1 < s.t. E [j b t B1 c ( p ) k k p N

k ,t k {z
k +1

1,k

for 0 1

bk

1

}

A. Doucet (MLSS Sept. 2012)

Sept. 2012

37 / 136

Putting Everything Together
Under such strong mixing assumptions bt t = |k ,t (bk ) t jp ]
1/p t

k =1

1 ' p t N

We can then obtain results such as there exists B1 < s.t. E [j b t B1 c ( p ) k k p N

k ,t k {z
k +1

1,k

for 0 1

bk

1

}

Much work has been done recently on removing such strong mixing assumptions; e.g. Whiteley (2012) for much weaker and realistic assumptions.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

37 / 136

Summary

SMC provide consistent estimates under weak assumptions.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

38 / 136

Summary

SMC provide consistent estimates under weak assumptions. Under stability assumptions, we have uniform in time stability of the SMC estimates of fp ( xt j y1:t )gt 1 .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

38 / 136

Summary

SMC provide consistent estimates under weak assumptions. Under stability assumptions, we have uniform in time stability of the SMC estimates of fp ( xt j y1:t )gt 1 . Under stability assumptions, the relative variance of the SMC estimate of fp (y1:t )gt 1 only increases linearly with t.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

38 / 136

Summary

SMC provide consistent estimates under weak assumptions. Under stability assumptions, we have uniform in time stability of the SMC estimates of fp ( xt j y1:t )gt 1 . Under stability assumptions, the relative variance of the SMC estimate of fp (y1:t )gt 1 only increases linearly with t.

Even under stability assumptions, one cannot expect to obtain uniform in time stability for SMC estimates of fp ( x1:t j y1:t )gt is due to the degeneracy problem.

1

; this

A. Doucet (MLSS Sept. 2012)

Sept. 2012

38 / 136

Summary

SMC provide consistent estimates under weak assumptions. Under stability assumptions, we have uniform in time stability of the SMC estimates of fp ( xt j y1:t )gt 1 . Under stability assumptions, the relative variance of the SMC estimate of fp (y1:t )gt 1 only increases linearly with t.

Even under stability assumptions, one cannot expect to obtain uniform in time stability for SMC estimates of fp ( x1:t j y1:t )gt is due to the degeneracy problem.

1

; this

Is it possible to Q1: eliminate, Q2: mitigate the degeneracy problem?

A. Doucet (MLSS Sept. 2012)

Sept. 2012

38 / 136

Summary

SMC provide consistent estimates under weak assumptions. Under stability assumptions, we have uniform in time stability of the SMC estimates of fp ( xt j y1:t )gt 1 . Under stability assumptions, the relative variance of the SMC estimate of fp (y1:t )gt 1 only increases linearly with t.

Even under stability assumptions, one cannot expect to obtain uniform in time stability for SMC estimates of fp ( x1:t j y1:t )gt is due to the degeneracy problem. Answer: Q1: no, Q2: yes.

1

; this

Is it possible to Q1: eliminate, Q2: mitigate the degeneracy problem?

A. Doucet (MLSS Sept. 2012)

Sept. 2012

38 / 136

Is Resampling Really Necessary?

Resampling is the source of the degeneracy problem and might appear wasteful.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

39 / 136

Is Resampling Really Necessary?

Resampling is the source of the degeneracy problem and might appear wasteful. The resampling step is an unbiased operation E [ p ( x1:t j y1:t )j p ( x1:t j y1:t )] = p ( x1:t j y1:t ) b e e V
Z

but clearly it introduces some errors locally in time. That is for any test function, we have V
Z

(x1:t ) p ( x1:t j y1:t ) dx1:t b

(x1:t ) p ( x1:t j y1:t ) dx1:t e

A. Doucet (MLSS Sept. 2012)

Sept. 2012

39 / 136

Is Resampling Really Necessary?

Resampling is the source of the degeneracy problem and might appear wasteful. The resampling step is an unbiased operation E [ p ( x1:t j y1:t )j p ( x1:t j y1:t )] = p ( x1:t j y1:t ) b e e V
Z

but clearly it introduces some errors locally in time. That is for any test function, we have V
Z

What about eliminating the resampling step?

(x1:t ) p ( x1:t j y1:t ) dx1:t b

(x1:t ) p ( x1:t j y1:t ) dx1:t e

A. Doucet (MLSS Sept. 2012)

Sept. 2012

39 / 136

Sequential Importance Samping: SMC Without Resampling
In this case, the estimate of the posterior is pSIS ( x1:t j y1:t ) = b p y1:t j X1:t
(i )
N

i =1

Wt
t

(i )

X (i ) (x1:t )
1:t

where X1:t

(i )

p (x1:t ) and Wt
(i )

k =1

g

yk j Xt

(i )

.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

40 / 136

Sequential Importance Samping: SMC Without Resampling
In this case, the estimate of the posterior is pSIS ( x1:t j y1:t ) = b p y1:t j X1:t
(i )
N

i =1

Wt
t

(i )

X (i ) (x1:t )
1:t

where X1:t

(i )

p (x1:t ) and Wt
(i )

k =1

g

yk j Xt

(i )

.

In this case, the marginal likelihood estimate is pSIS (y1:t ) = b 1 N

i =1

p

N

y1:t j X1:t

(i )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

40 / 136

Sequential Importance Samping: SMC Without Resampling
In this case, the estimate of the posterior is pSIS ( x1:t j y1:t ) = b p y1:t j X1:t
(i )
N

i =1

Wt
t

(i )

X (i ) (x1:t )
1:t

where X1:t

(i )

p (x1:t ) and Wt
(i )

k =1

g

yk j Xt

(i )

.

In this case, the marginal likelihood estimate is pSIS (y1:t ) = b 1 N

i =1

p
t

N

y1:t j X1:t

(i )

Relative variance of p y1:t j X1:t exponentially fast...
A. Doucet (MLSS Sept. 2012)

(i )

=

k =1

g

yk j Xt

(i )

is increasing

Sept. 2012

40 / 136

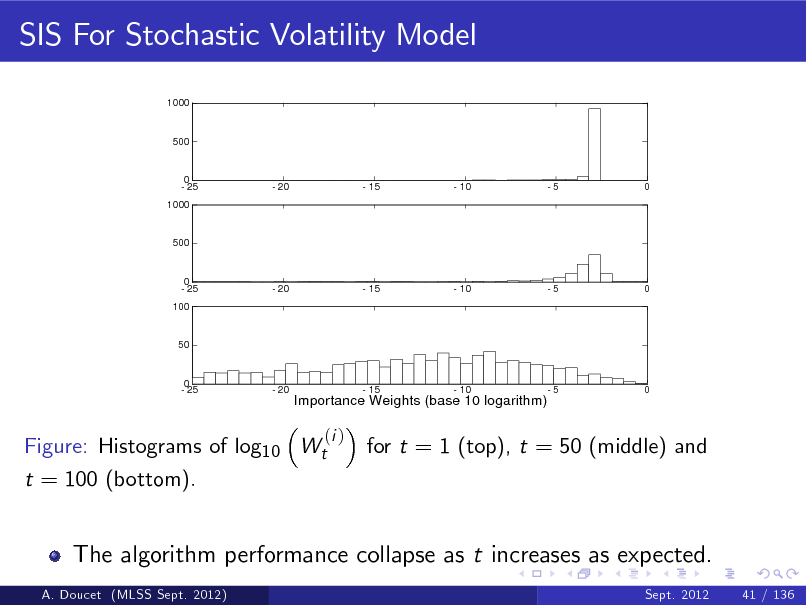
SIS For Stochastic Volatility Model
1000

500

0 - 25 1000

- 20

- 15

- 10

-5

0

500

0 - 25 100

- 20

- 15

- 10

-5

0

50

0 - 25

- 20

Importance Weights (base 10 logarithm)

- 15

- 10

-5

0

Figure: Histograms of log10 Wt t = 100 (bottom).

(i )

for t = 1 (top), t = 50 (middle) and

The algorithm performance collapse as t increases as expected.
A. Doucet (MLSS Sept. 2012) Sept. 2012 41 / 136

Central Limit Theorems
For both SIS and SMC, we have a CLT for the estimates of the marginal likelihood

p p

N

N

pSIS (y1:t ) b p (y1:t ) pSMC (y1:t ) b p (y1:t )

1 1

) N 0, 2 t,SIS , ) N 0, 2 t,SMC .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

42 / 136

Central Limit Theorems
For both SIS and SMC, we have a CLT for the estimates of the marginal likelihood

p p

N

N

The variance expressions are 2 t,SIS =

pSIS (y1:t ) b p (y1:t ) pSMC (y1:t ) b p (y1:t )

1 1

) N 0, 2 t,SIS , ) N 0, 2 t,SMC .

2 t,SMC =

R

=

R 2 p ( y1:t jx1:t )p (x1:t )dx1:t p 2 ( x1:t jy1:t ) dx1:t 1 = 1 p (x1:t ) p 2 (y1:t ) R R p 2 ( x1 jy1:t ) 2( x p 1:k jy 1:t ) dx1 + t =2 p ( x dx1:k k R 2 (x 1 ) R 21:k 1 jy1:k 1 )f ( xk jxk 1 ) g ( y1 jx1 )(x1 )dx1 p ( yk :t jxk )p ( xk jy1:k 1 )dxk + t =2 t k p 2 (y 1 ) p 2 ( yk :t jy1:k 1 )

t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

42 / 136

Central Limit Theorems
For both SIS and SMC, we have a CLT for the estimates of the marginal likelihood

p p

N

N

The variance expressions are 2 t,SIS =

pSIS (y1:t ) b p (y1:t ) pSMC (y1:t ) b p (y1:t )

1 1

) N 0, 2 t,SIS , ) N 0, 2 t,SMC .

2 t,SMC =

R

=

R 2 p ( y1:t jx1:t )p (x1:t )dx1:t p 2 ( x1:t jy1:t ) dx1:t 1 = 1 p (x1:t ) p 2 (y1:t ) R R p 2 ( x1 jy1:t ) 2( x p 1:k jy 1:t ) dx1 + t =2 p ( x dx1:k k R 2 (x 1 ) R 21:k 1 jy1:k 1 )f ( xk jxk 1 ) g ( y1 jx1 )(x1 )dx1 p ( yk :t jxk )p ( xk jy1:k 1 )dxk + t =2 t k p 2 (y 1 ) p 2 ( yk :t jy1:k 1 )

t

SMC breaks the integral over X t into t integrals over X .
A. Doucet (MLSS Sept. 2012) Sept. 2012 42 / 136

A Toy Example
Consider the case where f ( x 0 j x ) = (x 0 ) = N x 0 ; 0, 2 and 1 g ( y j x ) = N y ; 0, 1 2 where 2 > 1.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

43 / 136

A Toy Example
Consider the case where f ( x 0 j x ) = (x 0 ) = N x 0 ; 0, 2 and 1 g ( y j x ) = N y ; 0, 1 2 where 2 > 1. Assume we observe y1 = V V pSIS (y1:t ) b p (y1:t )

=

pSMC (y1:t ) b p (y1:t )

= yt = 0 then we have " 2 1 4 t,SIS = N N 22 1 " 2 t 4 t,SMC = N N 22 1

t /2

1 ,
1/2

#

1 .

#

A. Doucet (MLSS Sept. 2012)

Sept. 2012

43 / 136

A Toy Example
Consider the case where f ( x 0 j x ) = (x 0 ) = N x 0 ; 0, 2 and 1 g ( y j x ) = N y ; 0, 1 2 where 2 > 1. Assume we observe y1 = V V pSIS (y1:t ) b p (y1:t )

=

pSMC (y1:t ) b p (y1:t )
2 t,SIS N

= yt = 0 then we have " 2 1 4 t,SIS = N N 22 1 " 2 t 4 t,SMC = N N 22 1
2

t /2

1 ,
1/2

#

1 . 1023 particles to

#

If select 2 = 1.2 then it is necessary to use N obtain

= 10

2

for t = 1000.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

43 / 136

A Toy Example
Consider the case where f ( x 0 j x ) = (x 0 ) = N x 0 ; 0, 2 and 1 g ( y j x ) = N y ; 0, 1 2 where 2 > 1. Assume we observe y1 = V V pSIS (y1:t ) b p (y1:t )

=

pSMC (y1:t ) b p (y1:t )
2 t,SIS N

= yt = 0 then we have " 2 1 4 t,SIS = N N 22 1 " 2 t 4 t,SMC = N N 22 1
2

t /2

1 ,
1/2

#

1 . 1023 particles to

#

If select 2 = 1.2 then it is necessary to use N obtain

= 10

2

for t = 1000. 104 particles:

To obtain N = 10 2 , SMC requires only N improvement by 19 orders of magnitude!
A. Doucet (MLSS Sept. 2012)

2 t,SMC

Sept. 2012

43 / 136

Better Resampling Schemes
h i (i ) (i ) Better resampling steps can be designed such that E Nt = NWt h i (i ) (i ) (i ) but V Nt < NWt 1 Wt ; residual resampling, minimal entropy resampling etc. (Capp et al., 2005).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

44 / 136

Better Resampling Schemes
h i (i ) (i ) Better resampling steps can be designed such that E Nt = NWt h i (i ) (i ) (i ) but V Nt < NWt 1 Wt ; residual resampling, minimal entropy resampling etc. (Capp et al., 2005). j k 1:N (i ) e (i ) Residual Resampling. Set Nt = NWt , sample N t from a
(1:N ) (i )

multinomial of parameters N, W t
(i ) Wt

where

Wt

(i )

N

1 N (i ) et

then set Nt

(i ) e (i ) = Nt + N t .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

44 / 136

Better Resampling Schemes
h i (i ) (i ) Better resampling steps can be designed such that E Nt = NWt h i (i ) (i ) (i ) but V Nt < NWt 1 Wt ; residual resampling, minimal entropy resampling etc. (Capp et al., 2005). j k 1:N (i ) e (i ) Residual Resampling. Set Nt = NWt , sample N t from a
(1:N ) (i )

multinomial of parameters N, W t
(i ) Wt

where

(i ) e (i ) = Nt + N t . 1 Systematic Resampling. Sample U1 U 0, N and dene Ui = U1 + i N1 for i = 2, ..., N, then set n o (k ) (k ) Nti = Uj : ik =11 Wt Uj with the convention ik =1 Wt

Wt

(i )

N

1 N (i ) et

then set Nt

0 =1 := 0. k

A. Doucet (MLSS Sept. 2012)

Sept. 2012

44 / 136

Measuring Variability of the Weights
To measure the variation of the weights, we can use the Eective Sample Size (ESS) ! 1 ESS =
i =1

N

Wt

(i ) 2

A. Doucet (MLSS Sept. 2012)

Sept. 2012

45 / 136

Measuring Variability of the Weights
To measure the variation of the weights, we can use the Eective Sample Size (ESS) ! 1 ESS =
(i )
i =1

N

Wt

(i ) 2

We have ESS = N if Wt (j ) and Wt = 1 for j 6= i.

= 1/N for any i and ESS = 1 if Wt

(i )

=1

A. Doucet (MLSS Sept. 2012)

Sept. 2012

45 / 136

Measuring Variability of the Weights
To measure the variation of the weights, we can use the Eective Sample Size (ESS) ! 1 ESS =
(i )
i =1

N

Wt

(i ) 2

We have ESS = N if Wt = 1/N for any i and ESS = 1 if Wt = 1 (j ) and Wt = 1 for j 6= i. Liu (1996) showed that for simple importance sampling for regular enough ! ! N 1 ESS (i ) (i ) (i ) V Wt Xt Vp ( x1:t jy1:t ) Xt ; ESS i i =1 =1 i.e. the estimate is roughly as accurate as using an iid sample of size ESS from p ( x1:t j y1:t ).
A. Doucet (MLSS Sept. 2012) Sept. 2012 45 / 136

(i )

Dynamic Resampling

Resampling at each time step can be harmful: only resample when necessary.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

46 / 136

Dynamic Resampling

Resampling at each time step can be harmful: only resample when necessary. Dynamic Resampling: If the variation of the weights as measured by ESS is too high, e.g. ESS < N/2, then resample the particles.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

46 / 136

Dynamic Resampling

Resampling at each time step can be harmful: only resample when necessary. Dynamic Resampling: If the variation of the weights as measured by ESS is too high, e.g. ESS < N/2, then resample the particles. We can also use the entropy Ent =

i =1

Wt

N

(i )

log2 Wt

(i )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

46 / 136

Dynamic Resampling

Resampling at each time step can be harmful: only resample when necessary. Dynamic Resampling: If the variation of the weights as measured by ESS is too high, e.g. ESS < N/2, then resample the particles. We can also use the entropy Ent =

i =1

Wt
(i )

N

(i )

log2 Wt

(i )

We have Ent = log2 (N ) if Wt = 1/N for any i. We have Ent = 0 (i ) (j ) if Wt = 1 and Wt = 1 for j 6= i.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

46 / 136

Improving the Sampling Step
Bootstrap lter. Sample particles blindly according to the prior without taking into account the observation Very ine cient for vague prior/peaky likelihood.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

47 / 136

Improving the Sampling Step
Bootstrap lter. Sample particles blindly according to the prior without taking into account the observation Very ine cient for vague prior/peaky likelihood. Optimal proposal/Perfect adaptation. Implement the following alternative update-propagate Bayesian recursion Update Propagate where p ( xt j yt , xt
1)
tj t 1 1:t 1 j 1:t 1 p ( x1:t 1 j y1:t ) = p ( yt jy1:t 1 ) p ( x1:t j y1:t ) = p ( x1:t 1 j y1:t ) p ( xt j yt , xt

p( y x

)p ( x

y

)

1)

=

Much more e cient when applicable; e.g. f ( xt j xt 1 ) = N (xt ; (xt 1 ) , v ) , g ( yt j xt ) = N (yt ; xt , w ) .
A. Doucet (MLSS Sept. 2012) Sept. 2012 47 / 136

f ( xt j xt 1 ) g ( yt j xt p ( yt j xt 1 )

1)

A General Bayesian Recursion
Introduce an arbitrary proposal distribution q ( xt j yt , xt approximation to p ( xt j yt , xt 1 ) .
1 );

i.e. an

A. Doucet (MLSS Sept. 2012)

Sept. 2012

48 / 136

A General Bayesian Recursion
Introduce an arbitrary proposal distribution q ( xt j yt , xt approximation to p ( xt j yt , xt 1 ) . We have seen that p ( x1:t j y1:t ) = so clearly p ( x1:t j y1:t ) = where w (xt
1 , xt , yt ) 1 );

i.e. an

g ( yt j xt ) f ( xt j xt 1 ) p ( x1:t p ( yt j y1:t 1 )
1 , xt , yt ) q

1 j y1:t 1 )

w (xt

( xt j yt , xt p ( yt j y1:t

1 ) p ( x1:t 1 j y1:t 1 ) 1)

=

g ( yt j xt ) f ( xt j xt q ( xt j yt , xt 1 )

1)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

48 / 136

A General Bayesian Recursion
Introduce an arbitrary proposal distribution q ( xt j yt , xt approximation to p ( xt j yt , xt 1 ) . We have seen that p ( x1:t j y1:t ) = so clearly p ( x1:t j y1:t ) = where w (xt
1 , xt , yt ) 1 );

i.e. an

g ( yt j xt ) f ( xt j xt 1 ) p ( x1:t p ( yt j y1:t 1 )
1 , xt , yt ) q

1 j y1:t 1 )

w (xt

( xt j yt , xt p ( yt j y1:t

1 ) p ( x1:t 1 j y1:t 1 ) 1)

=

This suggests a more general SMC algorithm.
A. Doucet (MLSS Sept. 2012)

g ( yt j xt ) f ( xt j xt q ( xt j yt , xt 1 )

1)

Sept. 2012

48 / 136

A General SMC Algorithm
Assume we have N weighted particles p ( x1:t e (i ) Sample Xt
1 j y1:t 1 )

then at time t, q xt j yt , Xt
(i ) 1
N

n

Wt

(i ) (i ) 1 , X1:t 1

o

approximating

p ( x1:t j y1:t ) = e
(i ) Wt

i =1

Wt

(i ) e (i ) e (i ) , set X1:t = X1:t 1 , Xt (i )

and

(i ) Wt 1

f

X (i ) (x1:t ) , e
1:t

e (i ) (i ) Xt Xt 1 g

(i ) e (i ) q Xt yt , Xt 1

e (i ) yt j Xt

.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

49 / 136

A General SMC Algorithm
Assume we have N weighted particles p ( x1:t e (i ) Sample Xt
1 j y1:t 1 )

then at time t, q xt j yt , Xt
(i ) 1
N

n

Wt

(i ) (i ) 1 , X1:t 1

o

approximating

p ( x1:t j y1:t ) = e
(i ) Wt

i =1

Wt

(i ) e (i ) e (i ) , set X1:t = X1:t 1 , Xt (i )

and

(i ) Wt 1

f

X (i ) (x1:t ) , e
1:t

e (i ) (i ) Xt Xt 1 g

If ESS< N/2 resample X1:t p ( x1:t j y1:t ) and set Wt e N 1 obtain p ( x1:t j y1:t ) = N i =1 X (i ) (x1:t ). b
1:t A. Doucet (MLSS Sept. 2012)

(i )

(i ) e (i ) q Xt yt , Xt 1

e (i ) yt j Xt
(i )

.

1 N

to

Sept. 2012

49 / 136

Building Proposals
Our aim is to select q ( xt j yt , xt 1 ) as close as possible to p ( xt j yt , xt 1 ) as this minimizes the variance of w (xt
1 , xt , yt )

=

g ( yt j xt ) f ( xt j xt q ( xt j yt , xt 1 )

1)

.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

50 / 136

Building Proposals
Our aim is to select q ( xt j yt , xt 1 ) as close as possible to p ( xt j yt , xt 1 ) as this minimizes the variance of w (xt
1 , xt , yt )

=

Example - EKF proposal: Let Xt = ( Xt with Vt Yt

g ( yt j xt ) f ( xt j xt q ( xt j yt , xt 1 )

1)

.

1 ) + Vt ,

Yt = (Xt ) + Wt ,

N (0, v ), Wt
( (Xt
1 )) +

(x ) x

N (0, w ). We perform local linearization ( Xt
(X t
1)

( Xt

1 )) + Wt

and use as a proposal. q ( xt j yt , xt
1)

g ( yt j xt ) f ( xt j xt b

1) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

50 / 136

Building Proposals
Our aim is to select q ( xt j yt , xt 1 ) as close as possible to p ( xt j yt , xt 1 ) as this minimizes the variance of w (xt
1 , xt , yt )

=

Example - EKF proposal: Let Xt = ( Xt with Vt Yt

g ( yt j xt ) f ( xt j xt q ( xt j yt , xt 1 )

1)

.

1 ) + Vt ,

Yt = (Xt ) + Wt ,

N (0, v ), Wt
( (Xt
1 )) +

(x ) x

N (0, w ). We perform local linearization ( Xt
(X t
1)

( Xt

1 )) + Wt

and use as a proposal. q ( xt j yt , xt
1)

Any standard suboptimal ltering methods can be used: Unscented Particle lter, Gaussan Quadrature particle lter etc.
A. Doucet (MLSS Sept. 2012) Sept. 2012 50 / 136

g ( yt j xt ) f ( xt j xt b

1) .

Implicit Proposals
Proposed recently by Chorin (2012). Let F (xt and
1 , xt )

= log g ( yt j xt ) + log f ( xt j xt
1 , xt )

1)

xt = arg max F (xt

= arg max p ( xt j yt , xt

1)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

51 / 136

Implicit Proposals
Proposed recently by Chorin (2012). Let F (xt and
1 , xt )

= log g ( yt j xt ) + log f ( xt j xt
1 , xt )

1)

= arg max p ( xt j yt , xt 1 ) We sample Z N (0, Inx ), then we solve in Xt 1 F (xt 1 , xt ) F (xt 1 , Xt ) = Z T Z , Z N (0, Inx ) 2 so if there is a unique solution
q ( xt j yt , xt
1)

xt = arg max F (xt

= pZ (z ) jdet z/xt j exp ( F (xt 1 , xt )) g ( yt j xt ) f ( xt j xt jdet xt /z j

1)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

51 / 136

Implicit Proposals
Proposed recently by Chorin (2012). Let F (xt and
1 , xt )

= log g ( yt j xt ) + log f ( xt j xt
1 , xt )

1)

= arg max p ( xt j yt , xt 1 ) We sample Z N (0, Inx ), then we solve in Xt 1 F (xt 1 , xt ) F (xt 1 , Xt ) = Z T Z , Z N (0, Inx ) 2 so if there is a unique solution = pZ (z ) jdet z/xt j exp ( F (xt 1 , xt )) g ( yt j xt ) f ( xt j xt jdet xt /z j The incremental weight is g ( yt j xt ) f ( xt j xt 1 ) jdet xt /z j exp (F (xt 1 , xt )) q ( xt j yt , xt 1 )
q ( xt j yt , xt
1)
Sept. 2012

xt = arg max F (xt

1)

A. Doucet (MLSS Sept. 2012)

51 / 136

Auxiliary Particle Filters

Popular variation introduced by (Pitt & Shephard, 1999).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

52 / 136

Auxiliary Particle Filters

Popular variation introduced by (Pitt & Shephard, 1999). This corresponds to a standard SMC algorithm (Johansen & D., 2008) where we target p ( x1:t j y1:t +1 ) p ( x1:t j y1:t ) p ( yt +1 j xt ) b b

where p ( yt +1 j xt ) b

b p ( yt +1 j xt ) using a proposal p ( xt j yt , xt

1 ).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

52 / 136

Auxiliary Particle Filters

Popular variation introduced by (Pitt & Shephard, 1999). This corresponds to a standard SMC algorithm (Johansen & D., 2008) where we target p ( x1:t j y1:t +1 ) p ( x1:t j y1:t ) p ( yt +1 j xt ) b b

When p ( yt +1 j xt ) = p ( yt +1 j xt ) and b p ( xt +1 j yt +1 , xt ) = p ( xt +1 j yt +1 , xt ) then we are back to perfect b adaptation.

where p ( yt +1 j xt ) b

b p ( yt +1 j xt ) using a proposal p ( xt j yt , xt

1 ).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

52 / 136

Block Sampling Proposals
Problem: we only sample Xt at time t so, even if you use p ( xt j yt , xt 1 ), the SMC estimates could have high variance if Vp ( xt 1 jy1:t 1 ) [p ( yt j xt 1 )] is high.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

53 / 136

Block Sampling Proposals
Problem: we only sample Xt at time t so, even if you use p ( xt j yt , xt 1 ), the SMC estimates could have high variance if Vp ( xt 1 jy1:t 1 ) [p ( yt j xt 1 )] is high. Block sampling idea: allows yourself to sample again Xt L +1:t 1 as well as Xt in light of yt . Optimally we would like at time t to sample Xt and
(i ) Wt (i ) L +1:t

p xt

(i ) L +1:t j yt L +1:t , Xt L

(i ) Wt 1

p X1:t y1:t p X1:t
(i )
L

(i )

y1:t

1

p Xt

(i ) L +1:t

yt

(i ) L +1:t , Xt L

Wt

(i ) 1p

yt j yt

(i ) L +1:t 1 , Xt L

A. Doucet (MLSS Sept. 2012)

Sept. 2012

53 / 136

Block Sampling Proposals
Problem: we only sample Xt at time t so, even if you use p ( xt j yt , xt 1 ), the SMC estimates could have high variance if Vp ( xt 1 jy1:t 1 ) [p ( yt j xt 1 )] is high. Block sampling idea: allows yourself to sample again Xt L +1:t 1 as well as Xt in light of yt . Optimally we would like at time t to sample Xt and
(i ) Wt (i ) L +1:t

p xt

(i ) L +1:t j yt L +1:t , Xt L

(i ) Wt 1

p X1:t y1:t p X1:t
(i )
L

(i )

y1:t

1

p Xt

(i ) L +1:t

yt

(i ) L +1:t , Xt L

Wt

(i ) 1p

yt j yt

(i ) L +1:t 1 , Xt L

When p ( xt L +1:t j yt L +1:t , xt L ) and p ( yt j yt L +1:t 1 , xt L ) are not available, we can use analytical approximations of them and still have consistent estimates (D., Briers & Senecal, 2006).
A. Doucet (MLSS Sept. 2012) Sept. 2012 53 / 136

Block Sampling Proposals
Computational cost is increased from O (N ) to O (LN ) so is it worth it?

A. Doucet (MLSS Sept. 2012)

Sept. 2012

54 / 136

Block Sampling Proposals
Computational cost is increased from O (N ) to O (LN ) so is it worth it? Consider the ideal scenario where Xt Yt where X1

= Xt 1 + Vt = Xt + W t
i.i.d.

N (0, 1) and Vt , Wt

N (0, 1).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

54 / 136

Block Sampling Proposals
Computational cost is increased from O (N ) to O (LN ) so is it worth it? Consider the ideal scenario where Xt Yt

= Xt 1 + Vt = Xt + W t
i.i.d.

where X1 N (0, 1) and Vt , Wt In this case, we have

N (0, 1). < c jxt
L

jp (yt jyt

L +1:t 1 , xt L )

p (yt jyt

0 L +1:t 1 , xt L )j

xt0

L j /2

L

where the rate of exponential convergence depends upon the signal-to-noise ratio if more general Gaussian AR are considered.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

54 / 136

Block Sampling Proposals
Computational cost is increased from O (N ) to O (LN ) so is it worth it? Consider the ideal scenario where Xt Yt

= Xt 1 + Vt = Xt + W t
i.i.d.

where X1 N (0, 1) and Vt , Wt In this case, we have

N (0, 1). < c jxt
L

jp (yt jyt

L +1:t 1 , xt L )

p (yt jyt

0 L +1:t 1 , xt L )j

xt0

L j /2

L

where the rate of exponential convergence depends upon the signal-to-noise ratio if more general Gaussian AR are considered. We can obtain an analytic expression of the variance of the (normalized) weight.
A. Doucet (MLSS Sept. 2012) Sept. 2012 54 / 136

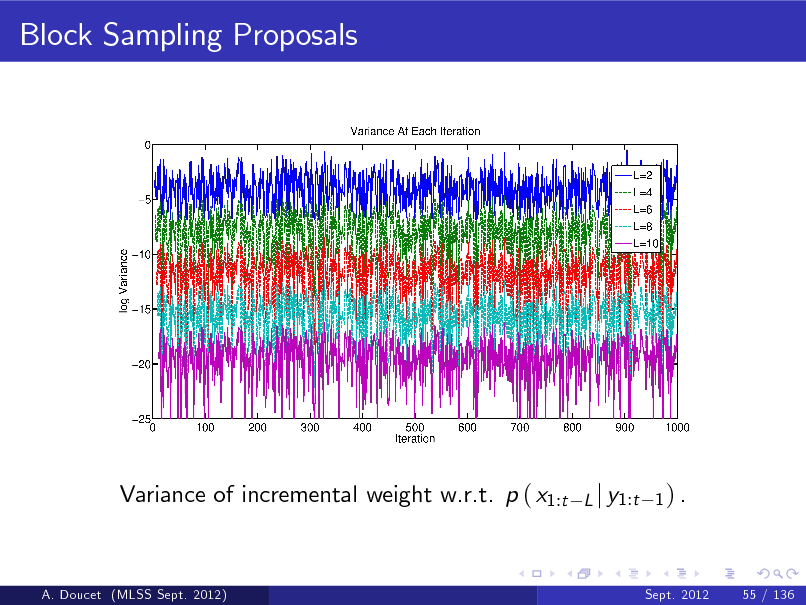
Block Sampling Proposals

Variance of incremental weight w.r.t. p ( x1:t

L j y1:t 1 ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

55 / 136

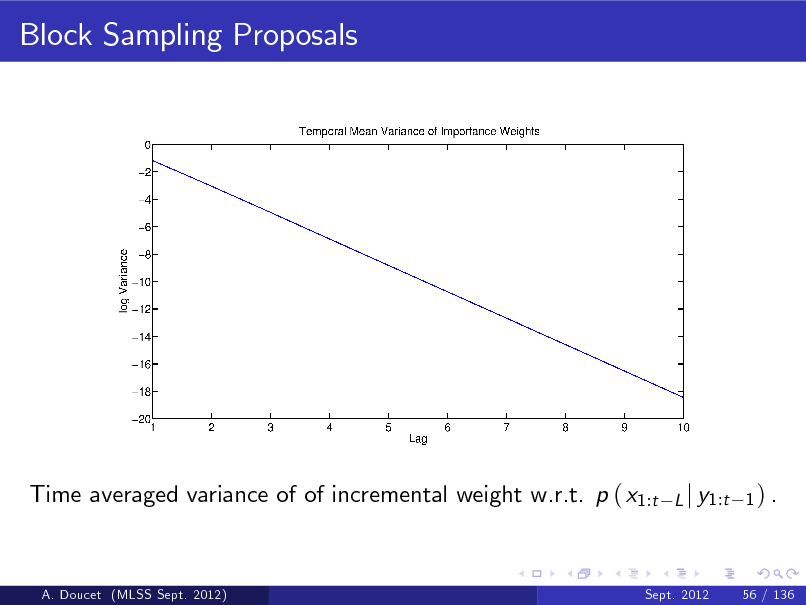
Block Sampling Proposals

Time averaged variance of of incremental weight w.r.t. p ( x1:t

L j y1:t 1 ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

56 / 136

Fighting Degeneracy Using MCMC Steps
The design of good proposals can be complicated and/or time consuming so, after the resampling step, a few particles might inherit many ospring.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

57 / 136

Fighting Degeneracy Using MCMC Steps
The design of good proposals can be complicated and/or time consuming so, after the resampling step, a few particles might inherit many ospring. A standard way to limit degeneracy is known as the Resample-Move algorithm (Gilks & Berzuini, 2001); i.e. using MCMC kernels as a principled way to jitter the particle locations.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

57 / 136

Fighting Degeneracy Using MCMC Steps
The design of good proposals can be complicated and/or time consuming so, after the resampling step, a few particles might inherit many ospring. A standard way to limit degeneracy is known as the Resample-Move algorithm (Gilks & Berzuini, 2001); i.e. using MCMC kernels as a principled way to jitter the particle locations.
0 A MCMC kernel Kt ( x1:t j x1:t ) of invariant distribution p ( x1:t j y1:t ) is a Markov transition kernel with the property that 0 p x1:t y1:t =

Z

0 p ( x1:t j y1:t ) Kt x1:t x1:t dx1:t , 0 Kt ( x1:t j X1:t ) then

0 i.e. if X1:t p ( x1:t j y1:t ) and X1:t j X1:t 0 marginally X1:t p ( x1:t j y1:t ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

57 / 136

Fighting Degeneracy Using MCMC Steps
0 Example 1: Gibbs moves. Set X1:t L = X1:t L then sample Xt0 L +1 0 ,x from p xt L +1 j yt L +1 , xt L t L +2 , sample Xt0 L +2 from p xt L +2 j yt L +2 , xt0 L +1 , xt L +3 and so on until we sample Xt0 from p xt j yt , xt0 1 ; that is 0 Kt x1:t x1:t

= x1:t

L

0 x1:t

t 1

L 1

k =t L +1

0 0 p xk yk , xk

1 , xk +1

p xt0 yt , xt0

A. Doucet (MLSS Sept. 2012)

Sept. 2012

58 / 136

Fighting Degeneracy Using MCMC Steps
0 Example 1: Gibbs moves. Set X1:t L = X1:t L then sample Xt0 L +1 0 ,x from p xt L +1 j yt L +1 , xt L t L +2 , sample Xt0 L +2 from p xt L +2 j yt L +2 , xt0 L +1 , xt L +3 and so on until we sample Xt0 from p xt j yt , xt0 1 ; that is 0 Kt x1:t x1:t

= x1:t

L

0 x1:t

t 1

L 1

k =t L +1

0 0 p xk yk , xk

1 , xk +1

p xt0 yt , xt0

0 Example 2: Metropolis-Hastings moves. Set X1:t L = X1:t sample Xt L +1 from q xt0 L +1:t xt L , xt L +1:t and set Xt0 L +1 = Xt L +1 with proba.

L

then

1^

p xt p ( xt

L +1:t

otherwise set Xt0
A. Doucet (MLSS Sept. 2012)

yt L +1:t j yt
L +1

q xt L +1 , xt L ) q xt
L +1 .

L +1 , xt L

L +1:t j xt L , xt L +1:t L +1:t

xt

L , xt L +1:t

,

= Xt

Sept. 2012

58 / 136

Fighting Degeneracy Using MCMC Steps
0 Example 1: Gibbs moves. Set X1:t L = X1:t L then sample Xt0 L +1 0 ,x from p xt L +1 j yt L +1 , xt L t L +2 , sample Xt0 L +2 from p xt L +2 j yt L +2 , xt0 L +1 , xt L +3 and so on until we sample Xt0 from p xt j yt , xt0 1 ; that is 0 Kt x1:t x1:t

= x1:t

L

0 x1:t

t 1

L 1

k =t L +1

0 0 p xk yk , xk

1 , xk +1

p xt0 yt , xt0

0 Example 2: Metropolis-Hastings moves. Set X1:t L = X1:t sample Xt L +1 from q xt0 L +1:t xt L , xt L +1:t and set Xt0 L +1 = Xt L +1 with proba.

L

then

1^

p xt p ( xt

L +1:t

otherwise set Xt0 L +1 = Xt L +1 . Contrary to MCMC, we typically do not use ergodic kernels in SMC.
A. Doucet (MLSS Sept. 2012) Sept. 2012 58 / 136

yt L +1:t j yt

q xt L +1 , xt L ) q xt

L +1 , xt L

L +1:t j xt L , xt L +1:t L +1:t

xt

L , xt L +1:t

,

Example: Bearings-only-tracking
Target modelled using a standard constant velocity model Xt = AXt
i.i.d. 1

+ Vt

where Vt N (0, ). The state vector T 1 contains location and velocity Xt = Xt Xt2 Xt3 Xt4 components.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

59 / 136

Example: Bearings-only-tracking
Target modelled using a standard constant velocity model Xt = AXt
i.i.d. 1

+ Vt

where Vt N (0, ). The state vector T 1 contains location and velocity Xt = Xt Xt2 Xt3 Xt4 components. One only receives observations of the bearings of the target Yt = tan where Wt
i.i.d. 1

Xt3 Xt1

+ Wt

N 0, 10

4

; i.e. the observations are almost noiseless.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

59 / 136

Example: Bearings-only-tracking
Target modelled using a standard constant velocity model Xt = AXt
i.i.d. 1

+ Vt

where Vt N (0, ). The state vector T 1 contains location and velocity Xt = Xt Xt2 Xt3 Xt4 components. One only receives observations of the bearings of the target Yt = tan where Wt
i.i.d. 1

Xt3 Xt1

+ Wt

N 0, 10 4 ; i.e. the observations are almost noiseless. We compare Bootstrap lter, SMC-EKF with L = 5, 10, MCMC moves L = 5, 10 using dynamic resampling.
Sept. 2012 59 / 136

A. Doucet (MLSS Sept. 2012)

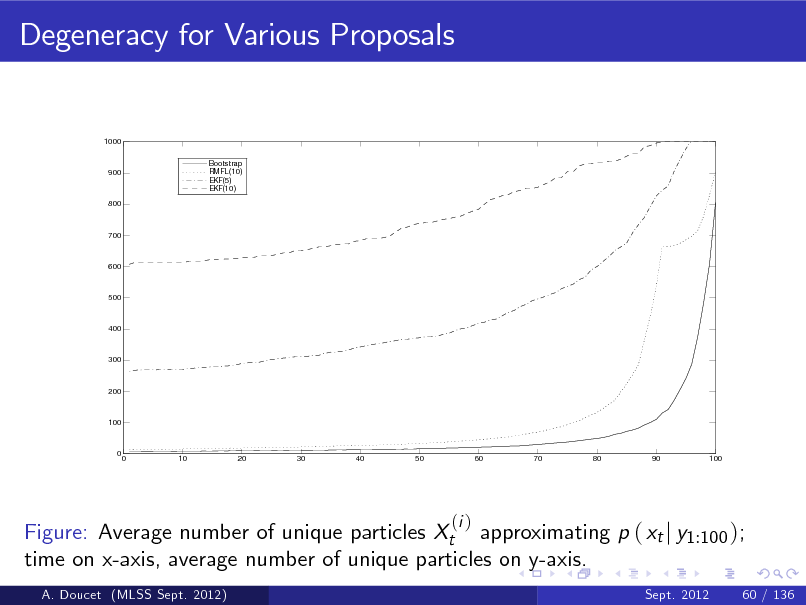
Degeneracy for Various Proposals

1000 Bootstrap RMFL(10) EKF(5) EKF(10)

900

800

700

600

500

400

300

200

100

0

0

10

20

30

40

50

60

70

80

90

100

Figure: Average number of unique particles Xt approximating p ( xt j y1 :100 ); time on x-axis, average number of unique particles on y-axis.
A. Doucet (MLSS Sept. 2012) Sept. 2012 60 / 136

(i )

Summary

SMC provide consistent estimates under weak assumptions.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

61 / 136

Summary

SMC provide consistent estimates under weak assumptions. We can estimate fp ( xt j y1:t )gt 1 satisfactorily but our approximations of fp ( x1:t j y1:t )gt 1 degenerates as t increases because of resampling steps.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

61 / 136

Summary

SMC provide consistent estimates under weak assumptions. We can estimate fp ( xt j y1:t )gt 1 satisfactorily but our approximations of fp ( x1:t j y1:t )gt 1 degenerates as t increases because of resampling steps. Resampling is crucial.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

61 / 136

Summary

SMC provide consistent estimates under weak assumptions. We can estimate fp ( xt j y1:t )gt 1 satisfactorily but our approximations of fp ( x1:t j y1:t )gt 1 degenerates as t increases because of resampling steps. Resampling is crucial. We can mitigate but not eliminate the degeneracy problem by the design of clever proposals.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

61 / 136

Summary

SMC provide consistent estimates under weak assumptions. We can estimate fp ( xt j y1:t )gt 1 satisfactorily but our approximations of fp ( x1:t j y1:t )gt 1 degenerates as t increases because of resampling steps. Resampling is crucial. We can mitigate but not eliminate the degeneracy problem by the design of clever proposals. Smoothing methods to estimate p ( x1:T j y1:T ) can come to the rescue.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

61 / 136

Smoothing in State-Space Models

Smoothing problem: given a xed time T , we are interested in p ( x1:T j y1:T ) or some of its marginals, e.g. fp ( xt j y1:T )gT=1 . t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

62 / 136

Smoothing in State-Space Models

Smoothing problem: given a xed time T , we are interested in p ( x1:T j y1:T ) or some of its marginals, e.g. fp ( xt j y1:T )gT=1 . t Smoothing is crucial to parameter estimation.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

62 / 136

Smoothing in State-Space Models

Smoothing problem: given a xed time T , we are interested in p ( x1:T j y1:T ) or some of its marginals, e.g. fp ( xt j y1:T )gT=1 . t Smoothing is crucial to parameter estimation. Direct SMC approximations of p ( x1:T j y1:T ) and its marginals p ( xk j y1:T ) are poor if T is large.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

62 / 136

Smoothing in State-Space Models

Smoothing problem: given a xed time T , we are interested in p ( x1:T j y1:T ) or some of its marginals, e.g. fp ( xt j y1:T )gT=1 . t Smoothing is crucial to parameter estimation. Direct SMC approximations of p ( x1:T j y1:T ) and its marginals p ( xk j y1:T ) are poor if T is large.

SMC provide good approximations of marginals fp ( xt j y1:t )gt This can be used to develop e cient smoothing estimates. Fixed-lag smoothing Forward-backward smoothing (Generalized) two-lter smoothing

1.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

62 / 136

Fixed-Lag Smoothing
The xed-lag smoothing approximation relies on p ( xt j y1:T ) p ( xt j y1:t + ) for large enough.

and quantitative bounds can be established under stability assumptions.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

63 / 136

Fixed-Lag Smoothing
The xed-lag smoothing approximation relies on p ( xt j y1:T ) p ( xt j y1:t + ) for large enough.

and quantitative bounds can be established under stability assumptions. This can be exploited by SMC methods (Kitagawa & Sato, 2001)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

63 / 136

Fixed-Lag Smoothing
The xed-lag smoothing approximation relies on p ( xt j y1:T ) p ( xt j y1:t + ) for large enough.

and quantitative bounds can be established under stability assumptions. This can be exploited by SMC methods (Kitagawa & Sato, 2001) n o (i ) Algorithmically: stop resampling Xt beyond time t + (Kitagawa & Sato, 2001).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

63 / 136

Fixed-Lag Smoothing
The xed-lag smoothing approximation relies on p ( xt j y1:T ) p ( xt j y1:t + ) for large enough.

and quantitative bounds can be established under stability assumptions. This can be exploited by SMC methods (Kitagawa & Sato, 2001) n o (i ) Algorithmically: stop resampling Xt beyond time t + (Kitagawa & Sato, 2001). Computational cost is O (N ) but non-vanishing bias as N ! (Olsson & al., 2008).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

63 / 136

Fixed-Lag Smoothing
The xed-lag smoothing approximation relies on p ( xt j y1:T ) p ( xt j y1:t + ) for large enough.

and quantitative bounds can be established under stability assumptions. This can be exploited by SMC methods (Kitagawa & Sato, 2001) n o (i ) Algorithmically: stop resampling Xt beyond time t + (Kitagawa & Sato, 2001). Computational cost is O (N ) but non-vanishing bias as N ! (Olsson & al., 2008). Picking is di cult: too small results in p ( xt j y1:t + ) being a poor approximation of p ( xt j y1:T ). too large improves the approximation but degeneracy creeps in.
A. Doucet (MLSS Sept. 2012) Sept. 2012 63 / 136

Forward Backward Smoothing
Forward Backward (FB) decomposition states
T

p ( x1:T j y1:T ) = p ( xT j y1:T )

t =1 T 1 t =1

p ( xt j y1:T , xt +1:T ) p ( xt j y1:t , xt +1 )

1

= p ( xT j y1:T )
where p ( xt j y1:t , xt +1 ) =

f ( xt +1 j xt ) p ( xt j y1:t ) . p ( xt +1 j y1:t )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

64 / 136

Forward Backward Smoothing
Forward Backward (FB) decomposition states
T

p ( x1:T j y1:T ) = p ( xT j y1:T )

t =1 T 1 t =1

p ( xt j y1:T , xt +1:T ) p ( xt j y1:t , xt +1 )

1

= p ( xT j y1:T )
where p ( xt j y1:t , xt +1 ) =

Conditioned upon y1:T , fXt gT=1 is a backward Markov chain of initial t distribution p ( xT j y1:T ) and inhomogeneous Markov transitions fp ( xt j y1:t , xt +1 )gT=11 . t
A. Doucet (MLSS Sept. 2012) Sept. 2012 64 / 136

f ( xt +1 j xt ) p ( xt j y1:t ) . p ( xt +1 j y1:t )

Forward Filtering Backward Sampling
To obtain a sample from p ( x1:T j y1:T ) ,

A. Doucet (MLSS Sept. 2012)

Sept. 2012

65 / 136

Forward Filtering Backward Sampling
To obtain a sample from p ( x1:T j y1:T ) ,
Forward ltering: compute and store fp ( xt j y1 :t )gT=1 t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

65 / 136

Forward Filtering Backward Sampling
To obtain a sample from p ( x1:T j y1:T ) ,
Forward ltering: compute and store fp ( xt j y1 :t )gT=1 t Backward sampling: sample XT p ( xT j y1 :T ) then for t = T 1, ..., 1 sample Xt p ( xt j y1 :t , Xt +1 ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

65 / 136

Forward Filtering Backward Sampling
To obtain a sample from p ( x1:T j y1:T ) ,
Forward ltering: compute and store fp ( xt j y1 :t )gT=1 t Backward sampling: sample XT p ( xT j y1 :T ) then for t = T 1, ..., 1 sample Xt p ( xt j y1 :t , Xt +1 ) .

SMC to obtain an approximate sample from p ( x1:T j y1:T )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

65 / 136

Forward Filtering Backward Sampling
To obtain a sample from p ( x1:T j y1:T ) ,
Forward ltering: compute and store fp ( xt j y1 :t )gT=1 t Backward sampling: sample XT p ( xT j y1 :T ) then for t = T 1, ..., 1 sample Xt p ( xt j y1 :t , Xt +1 ) . Forward ltering: compute and store fp ( xt j y1 :t )gT=1 . b t

SMC to obtain an approximate sample from p ( x1:T j y1:T )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

65 / 136

Forward Filtering Backward Sampling
To obtain a sample from p ( x1:T j y1:T ) ,
Forward ltering: compute and store fp ( xt j y1 :t )gT=1 t Backward sampling: sample XT p ( xT j y1 :T ) then for t = T 1, ..., 1 sample Xt p ( xt j y1 :t , Xt +1 ) . Forward ltering: compute and store fp ( xt j y1 :t )gT=1 . b t Backward sampling: sample XT p ( xT j y1 :T ) then for b t = T 1, ..., 1 sample Xt p ( xt j y1 :t , Xt +1 ) where b p ( xt j y1 :t , Xt +1 ) b f ( Xt +1 j xt ) p ( xt j y1 :t ) b
i =1

SMC to obtain an approximate sample from p ( x1:T j y1:T )

f

N

Xt +1 j Xt

(i )

Xt

(i )

( xt )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

65 / 136

Forward Filtering Backward Sampling
To obtain a sample from p ( x1:T j y1:T ) ,
Forward ltering: compute and store fp ( xt j y1 :t )gT=1 t Backward sampling: sample XT p ( xT j y1 :T ) then for t = T 1, ..., 1 sample Xt p ( xt j y1 :t , Xt +1 ) . Forward ltering: compute and store fp ( xt j y1 :t )gT=1 . b t Backward sampling: sample XT p ( xT j y1 :T ) then for b t = T 1, ..., 1 sample Xt p ( xt j y1 :t , Xt +1 ) where b p ( xt j y1 :t , Xt +1 ) b f ( Xt +1 j xt ) p ( xt j y1 :t ) b
i =1

SMC to obtain an approximate sample from p ( x1:T j y1:T )

f

N

Xt +1 j Xt

(i )

Xt

(i )

( xt )

Direct implementation O (NT ) (Godsill, D. & West, 2004). Rejection sampling possible if f ( xt +1 j xt ) C (xt +1 ) (Douc et al., 2011) and cost O (NT ) .
A. Doucet (MLSS Sept. 2012) Sept. 2012 65 / 136

Forward Filtering Backward Smoothing
Assume you want to compute the marginal smoothing distributions fp ( xt j y1:T )gT=1 instead of sampling from them. t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

66 / 136

Forward Filtering Backward Smoothing
Assume you want to compute the marginal smoothing distributions fp ( xt j y1:T )gT=1 instead of sampling from them. t Forward ltering Backward smoothing (FFBS). z }| { p ( xt j y1:T )
smoother at t

= =

Z Z

p ( xt , xt +1 j y1:T ) dxt +1 p ( xt +1 j y1:T ) p ( xt j y1:t , xt +1 ) dxt +1 z }| { f ( xt +1 j xt ) p ( xt j y1:t ) dxt +1 . p ( xt +1 j y1:T ) p ( xt +1 j y1:t ) | {z }
backward transition p ( xt jy1:t ,xt +1 ) lter at t

=

smoother at t +1 Z z }| {

A. Doucet (MLSS Sept. 2012)

Sept. 2012

66 / 136

Forward Filtering Backward Smoothing
Assume you want to compute the marginal smoothing distributions fp ( xt j y1:T )gT=1 instead of sampling from them. t Forward ltering Backward smoothing (FFBS). z }| { p ( xt j y1:T )
smoother at t

= =

Z Z

p ( xt , xt +1 j y1:T ) dxt +1 p ( xt +1 j y1:T ) p ( xt j y1:t , xt +1 ) dxt +1 z }| { f ( xt +1 j xt ) p ( xt j y1:t ) dxt +1 . p ( xt +1 j y1:T ) p ( xt +1 j y1:t ) | {z }
backward transition p ( xt jy1:t ,xt +1 ) lter at t

=

smoother at t +1 Z z }| {

For nite state-space HMM, it is surprisingly and unfortunately not the recursion usually implemented (Rabiner et al., 1989).
A. Doucet (MLSS Sept. 2012) Sept. 2012

66 / 136

SMC Forward Filtering Backward Smoothing
Forward ltering: compute and store fp ( xt j y1:t )gT=1 using your b t favourite SMC.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

67 / 136

SMC Forward Filtering Backward Smoothing
Forward ltering: compute and store fp ( xt j y1:t )gT=1 using your b t favourite SMC. Backward smoothing: For t = T 1, ..., 1, we have (i ) (i ) p ( xt j y1:T ) = N 1 Wt jT X (i ) (xt ) with WT jT = 1/N and b i=
t 1 N

p ( xt j y1:T ) = p ( xt j y1:t ) b b | {z }
N 1 i=

(i ) ( x t ) Xt

R
t

N 1 W t +1 jT j=

= N 1 Wt jT X (i ) (xt ) i=
(i ) Wt j T

(i )

p ( xt +1 j y1:T ) b | {z }
(j )

(j ) ( x t +1 ) X t +1

R

f ( x t +1 j x t ) dxt +1 f ( xt +1 jxt )p ( xt jy1:t )dxt b

where

=

j =1

N

(j ) Wt +1 jT

f

Xt + 1 j Xt
(j )

(j )

(i ) (l )

N 1 f l=

.

Xt + 1 j Xt

A. Doucet (MLSS Sept. 2012)

Sept. 2012

67 / 136

SMC Forward Filtering Backward Smoothing
Forward ltering: compute and store fp ( xt j y1:t )gT=1 using your b t favourite SMC. Backward smoothing: For t = T 1, ..., 1, we have (i ) (i ) p ( xt j y1:T ) = N 1 Wt jT X (i ) (xt ) with WT jT = 1/N and b i=
t 1 N

p ( xt j y1:T ) = p ( xt j y1:t ) b b | {z }
N 1 i=

(i ) ( x t ) Xt

R
t

N 1 W t +1 jT j=

= N 1 Wt jT X (i ) (xt ) i=
(i ) Wt j T

(i )

p ( xt +1 j y1:T ) b | {z }
(j )

(j ) ( x t +1 ) X t +1

R

f ( x t +1 j x t ) dxt +1 f ( xt +1 jxt )p ( xt jy1:t )dxt b

where

=

j =1

N

(j ) Wt +1 jT

f

Xt + 1 j Xt
(j )

(j )

(i ) (l )

N 1 f l=

.

Xt + 1 j Xt

Computational complexity is O TN 2 .
A. Doucet (MLSS Sept. 2012) Sept. 2012 67 / 136

Two-Filter Smoothing
An alternative to FB smoothing is the Two-Filter (TF) formula z }| { z }| { p ( xt , xt +1 j y1:T ) p ( xt j y1:t )f ( xt +1 j xt ) p ( yt +1:T j xt +1 )
forward lter backward lter

A. Doucet (MLSS Sept. 2012)

Sept. 2012

68 / 136

Two-Filter Smoothing
An alternative to FB smoothing is the Two-Filter (TF) formula z }| { z }| { p ( xt , xt +1 j y1:T ) p ( xt j y1:t )f ( xt +1 j xt ) p ( yt +1:T j xt +1 )
Z
forward lter backward lter

The backward information lter satises p ( yT j xT ) = g ( yT j xT ) and p ( yt :T j xt ) = p ( yt , yt +1:T , xt +1 j xt ) dxt +1
Z

= g ( yt j xt )

p ( yt +1:T j xt +1 ) f ( xt +1 j xt ) dxt +1

A. Doucet (MLSS Sept. 2012)

Sept. 2012

68 / 136

Two-Filter Smoothing
An alternative to FB smoothing is the Two-Filter (TF) formula z }| { z }| { p ( xt , xt +1 j y1:T ) p ( xt j y1:t )f ( xt +1 j xt ) p ( yt +1:T j xt +1 )
Z
forward lter backward lter

The backward information lter satises p ( yT j xT ) = g ( yT j xT ) and p ( yt :T j xt ) = p ( yt , yt +1:T , xt +1 j xt ) dxt +1
Z

= g ( yt j xt )

p ( yt +1:T j xt +1 ) f ( xt +1 j xt ) dxt +1

Various particle methods have been proposed to approximate R fp ( yt :T j xt )gT=1 but rely implicitly on p ( yt :T j xt ) dxt < and try t to come up with a backward dynamics; e.g. solve Xt + 1 = ( Xt , Vt + 1 ) , Xt = This is incorrect.
A. Doucet (MLSS Sept. 2012) Sept. 2012 68 / 136

1

( Xt , Vt + 1 ) .

Generalized Two-Filter Smoothing
Generalized Two-Filter smoothing (Briers, D. & Maskell, 2004-2010) z }| { }| { z p ( xt j y1:t )f ( xt +1 j xt ) p ( xt +1 j yt +1:T ) p ( xt , xt +1 j y1:T ) p (xt +1 ) | {z }
articial prior forward lter backward lter

where

p ( xt +1 j yt +1:T ) p ( yt +1:T j xt +1 ) p (xt +1 ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

69 / 136

Generalized Two-Filter Smoothing
Generalized Two-Filter smoothing (Briers, D. & Maskell, 2004-2010) z }| { }| { z p ( xt j y1:t )f ( xt +1 j xt ) p ( xt +1 j yt +1:T ) p ( xt , xt +1 j y1:T ) p (xt +1 ) | {z }
articial prior forward lter backward lter

where

By construction, we now have integrable p ( xt +1 j yt +1:T ) which we can approximate using a backward SMC algorithm targeting fp ( xt +1:T j yt +1:T )g1=T where t p ( xt j yt :T ) p (xt )
A. Doucet (MLSS Sept. 2012)

p ( xt +1 j yt +1:T ) p ( yt +1:T j xt +1 ) p (xt +1 ) .

k =t +1

T

f ( xk j xk

1 ) g ( yk j xk ) . k =t
Sept. 2012 69 / 136

T

SMC Generalized Two-Filter Smoothing
Forward lter: compute and store fp ( xt j y1:t )gT=1 using your b t favourite SMC.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

70 / 136

SMC Generalized Two-Filter Smoothing
Forward lter: compute and store fp ( xt j y1:t )gT=1 using your b t favourite SMC. T b Backward lter: compute and store p ( xt j yt :T ) t =1 using your favourite SMC.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

70 / 136

SMC Generalized Two-Filter Smoothing
Forward lter: compute and store fp ( xt j y1:t )gT=1 using your b t favourite SMC. T b Backward lter: compute and store p ( xt j yt :T ) t =1 using your favourite SMC. Combination step: for any t 2 f1, ..., T g we have p ( xt , xt +1 j y1:T ) p ( xt j y1:T ) b b
i =1 j =1

N

N

f

X t + 1 Xt
(j )

f ( xt +1 j xt ) b p ( xt +1 j yt +1:t ) p (xt +1 )
(j ) (i )

p X t +1

X t ,X t +1

(i )

(j )

(xt , xt +1 ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

70 / 136

SMC Generalized Two-Filter Smoothing
Forward lter: compute and store fp ( xt j y1:t )gT=1 using your b t favourite SMC. T b Backward lter: compute and store p ( xt j yt :T ) t =1 using your favourite SMC. Combination step: for any t 2 f1, ..., T g we have p ( xt , xt +1 j y1:T ) p ( xt j y1:T ) b b
i =1 j =1

N

N

f

X t + 1 Xt
(j )

f ( xt +1 j xt ) b p ( xt +1 j yt +1:t ) p (xt +1 )
(j ) (i )

p X t +1

X t ,X t +1

(i )

(j )

(xt , xt +1 ) .

Cost O N 2 T but O (NT ) through importance sampling (Briers, D. & Singh, 2005; Fearnhead, Wyncoll & Tawn, 2010) and fast computational methods (Klaas et al., 2005).
A. Doucet (MLSS Sept. 2012) Sept. 2012 70 / 136

Convergence Results
0 Exponentially stability assumption. For any x1 , x1

1 2

Z

p ( xt j y2:t , X1 = x1 )

0 p xt j y2:t , X1 = x1

dxt

t for jj < 1.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

71 / 136

Convergence Results
0 Exponentially stability assumption. For any x1 , x1

1 2

Z

p ( xt j y2:t , X1 = x1 )

0 p xt j y2:t , X1 = x1

dxt

t for jj < 1.

Here b T denotes SMC estimates obtained using direct, xed-lag FB or TF method.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

71 / 136

Convergence Results
0 Exponentially stability assumption. For any x1 , x1

1 2

Z

p ( xt j y2:t , X1 = x1 )

0 p xt j y2:t , X1 = x1

dxt

t for jj < 1.

N !

Marginal distribution. If T (x1:T ) = (xt ), we have for the standard path-based SMC estimate p lim N ( b T T ) ) N 0, 2 , A (T t + 1) 2 A (T t + 1) T T
N !

Here b T denotes SMC estimates obtained using direct, xed-lag FB or TF method.

whereas for FB and TF estimates there exists B independent of T s.t. p lim N ( b T T ) ) N 0, 2 where 2 B T T
Sept. 2012 71 / 136

A. Doucet (MLSS Sept. 2012)

Comparison Direct Method vs FB and TF
Assume the model is stable and we are interested in approximating R T = (xt ) p ( xt j y1:T ) dxt using SMC. Fixed-lag N O (TN ) O (1/N ) 2 + O (1/N ) Direct SMC N O (TN ) O ((T t + 1) /N ) O (1/N ) O ((T t + 1) /N )

Method # particles cost Variance Bias MSE=Bias2 +Var

FB/TF N O TN 2 ,O (TN ) O (1/N ) O (1/N ) O (1/N )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

72 / 136

Comparison Direct Method vs FB and TF
Assume the model is stable and we are interested in approximating R T = (xt ) p ( xt j y1:T ) dxt using SMC. Fixed-lag N O (TN ) O (1/N ) 2 + O (1/N ) Direct SMC N O (TN ) O ((T t + 1) /N ) O (1/N ) O ((T t + 1) /N )

Method # particles cost Variance Bias MSE=Bias2 +Var

FB/TF N O TN 2 ,O (TN ) O (1/N ) O (1/N ) O (1/N )

FB/TF provide uniformly good approximations of fp ( xt j y1:T )gT=1 t whereas direct method provide only "good" approximation for jT t j "small.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

72 / 136

Comparison Direct Method vs FB and TF
Assume the model is stable and we are interested in approximating R T = (xt ) p ( xt j y1:T ) dxt using SMC. Fixed-lag N O (TN ) O (1/N ) 2 + O (1/N ) Direct SMC N O (TN ) O ((T t + 1) /N ) O (1/N ) O ((T t + 1) /N )

Method # particles cost Variance Bias MSE=Bias2 +Var

FB/TF N O TN 2 ,O (TN ) O (1/N ) O (1/N ) O (1/N )

FB/TF provide uniformly good approximations of fp ( xt j y1:T )gT=1 t whereas direct method provide only "good" approximation for jT t j "small. Fast implementations FB and TF of computational complexity O (NT ) outperform other approaches as MSE is O (1/N ) whereas it is O ((T t + 1) /N ) for direct SMC.
A. Doucet (MLSS Sept. 2012) Sept. 2012 72 / 136

Convergence Results for Smoothed Additive Functionals
Consider now the case where T (x1:T ) = T=1 (xt ) , so that t T
Z

= =

T (x1:T ) p ( x1:T j y1:T ) dx1:T
Z

t =1

T

(xt ) p ( xt j y1:T ) dxt

A. Doucet (MLSS Sept. 2012)

Sept. 2012

73 / 136

Convergence Results for Smoothed Additive Functionals
Consider now the case where T (x1:T ) = T=1 (xt ) , so that t T
Z

= =

T (x1:T ) p ( x1:T j y1:T ) dx1:T
Z

t =1

T

(xt ) p ( xt j y1:T ) dxt

This type of functionals is crucial when performing ML parameter estimation.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

73 / 136

Convergence Results for Smoothed Additive Functionals
Consider now the case where T (x1:T ) = T=1 (xt ) , so that t T
Z

= =

T (x1:T ) p ( x1:T j y1:T ) dx1:T
Z

t =1

T

(xt ) p ( xt j y1:T ) dxt

A. Doucet (MLSS Sept. 2012)

For the FB and TF estimates (Douc et al., 2009; Del Moral, D. & Singh, 2009), we have p lim N ( b T T ) ) N 0, 2 where 2 CT T T
N !
Sept. 2012

This type of functionals is crucial when performing ML parameter estimation. We have for the standard path-based SMC estimate (Poyiadjis, D. & Singh, 2010) p lim N ( b T T ) ) N 0, 2 where AT 2 2 AT 2 . T T
N !

73 / 136

Comparison Direct Method vs FB and TF
Assume we are interested in approximating R T = T=1 (xt ) p ( xt j y1:T ) dxt using SMC. t Fixed-lag N O (TN ) O (T /N ) T T 2 2 +O (T /N ) Direct SMC N O (TN ) O T 2 /N O (T /N ) O T 2 /N

Method # particles cost Var. Bias MSE=Bias2 +Var

FB/TF N O TN 2 , O (TN ) O (T /N ) O (T /N ) O T 2 /N 2

A. Doucet (MLSS Sept. 2012)

Sept. 2012

74 / 136

Comparison Direct Method vs FB and TF
Assume we are interested in approximating R T = T=1 (xt ) p ( xt j y1:T ) dxt using SMC. t Fixed-lag N O (TN ) O (T /N ) T T 2 2 +O (T /N ) Direct SMC N O (TN ) O T 2 /N O (T /N ) O T 2 /N

Method # particles cost Var. Bias MSE=Bias2 +Var

FB/TF N O TN 2 , O (TN ) O (T /N ) O (T /N ) O T 2 /N 2

Naive implementations FB and TF have MSE of same order as direct method for xed computational complexity but MSE is bias dominated for FB/TF whereas it is variance dominated for Direct SMC.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

74 / 136

Comparison Direct Method vs FB and TF
Assume we are interested in approximating R T = T=1 (xt ) p ( xt j y1:T ) dxt using SMC. t Fixed-lag N O (TN ) O (T /N ) T T 2 2 +O (T /N ) Direct SMC N O (TN ) O T 2 /N O (T /N ) O T 2 /N

Method # particles cost Var. Bias MSE=Bias2 +Var

FB/TF N O TN 2 , O (TN ) O (T /N ) O (T /N ) O T 2 /N 2

Naive implementations FB and TF have MSE of same order as direct method for xed computational complexity but MSE is bias dominated for FB/TF whereas it is variance dominated for Direct SMC. Fast implementations FB and TF of computational complexity O (NT ) outperform other approaches as MSE is O T 2 /N 2 whereas it is O T 2 /N for direct SMC.
A. Doucet (MLSS Sept. 2012) Sept. 2012 74 / 136

Experimental Results
Consider a linear Gaussian model Xt = 0.8Xt
1

+ 0.5Vt , Vt
i.i.d.

i.i.d.

N (0, 1)

Yt = Xt + Wt , Wt

N (0, 1) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

75 / 136

Experimental Results
Consider a linear Gaussian model Xt = 0.8Xt
1

+ 0.5Vt , Vt
i.i.d.

i.i.d.

N (0, 1)

Yt = Xt + Wt , Wt

N (0, 1) .

We simulate 10,000 observations and compute SMC estimates of
Z

T (x1:T ) p ( x1:T j y1:T ) dx1:T

for 4 dierent additive functionals t (x1:t ) = t 1 (x1:t 1 ) + (xt 1 , xt , yt ) including 1 (xt 1 , xt , yt ) = xt 1 xt , 2 (xt 1 , xt , yt ) = xt2 . [Ground truth can be computed using Kalman smoother.]

A. Doucet (MLSS Sept. 2012)

Sept. 2012

75 / 136

Experimental Results
Consider a linear Gaussian model Xt = 0.8Xt
1

+ 0.5Vt , Vt
i.i.d.

i.i.d.

N (0, 1)

Yt = Xt + Wt , Wt

N (0, 1) .

We simulate 10,000 observations and compute SMC estimates of
Z

T (x1:T ) p ( x1:T j y1:T ) dx1:T

for 4 dierent additive functionals t (x1:t ) = t 1 (x1:t 1 ) + (xt 1 , xt , yt ) including 1 (xt 1 , xt , yt ) = xt 1 xt , 2 (xt 1 , xt , yt ) = xt2 . [Ground truth can be computed using Kalman smoother.] We use SMC over 100 replications on the same dataset to estimate the empirical variance.
A. Doucet (MLSS Sept. 2012) Sept. 2012 75 / 136

Empirical Variance for Direct vs FB
V a r ia n c e o f s c o r e e s tim a te w .r .t.
x 10 10000 6 8000
4

v

V a r ia n c e o f s c o r e e s tim a te w .r .t.

V a r ia n c e o f s c o r e e s tim a te w .r .t.
v

V a r ia n c e o f s c o r e e s tim a te w .r .t.

120 100

60

V a ri a n c e

6000

V ariance

4

80 60 40

40

4000 2 2000

20

20 0 0 0 0

0 0

2500

5000

7500

10000

0 0

2500

5000

7500

10000

2500

5000

7500

10000

2500

5000

7500

10000

V a r ia n c e o f s c o r e e s tim a te w .r .t.
w

V a r ia n c e o f s c o r e e s tim a te w .r .t. c

V a r ia n c e o f s c o r e e s tim a te w .r .t.
w

V a r ia n c e o f s c o r e e s tim a te w .r .t. c

5000 4000 20 4000

40

30 3000

V a ri a n c e

V ariance

3000 2000 2000

15 20 10

1000

1000

5

10

0 0

2500

5000

7500

10000

0 0

2500

5000

7500

10000

0 0

2500

5000

7500

10000

0 0

2500

5000

7500

10000

T i m e s te p s

T i m e s te p s

T i m e s te p s

T i m e s te p s

Direct (left) vs FB (right); the vertical scale is dierent
A. Doucet (MLSS Sept. 2012) Sept. 2012 76 / 136

Boxplots of SMC Estimates for Direct vs FB
score estimates for parameter
Algorithm 1
500 500

v

Algorithm 2

Score

0

0

-500 2500 5000 7500 10000

-500 2500 5000 7500 10000

score estimates for parameter
Algorithm 1

Algorithm 2

200

200

Score

0

0

-200 2500 5000 7500 10000

-200 2500 5000 7500 10000

Time steps

Time steps

Direct (left) vs FB (right)
A. Doucet (MLSS Sept. 2012) Sept. 2012 77 / 136

Summary

SMC smoothing techniques allow us to solve the degeneracy problem.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

78 / 136

Summary

SMC smoothing techniques allow us to solve the degeneracy problem. SMC xed-lag smoothing is the simplest one but has non-vanishing bias di cult to quantify.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

78 / 136

Summary

SMC smoothing techniques allow us to solve the degeneracy problem. SMC xed-lag smoothing is the simplest one but has non-vanishing bias di cult to quantify. SMC FB and SMC TF algorithms provide uniformly good approximations of marginal smoothing distributions contrary to direct method.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

78 / 136

Summary

SMC smoothing techniques allow us to solve the degeneracy problem. SMC xed-lag smoothing is the simplest one but has non-vanishing bias di cult to quantify. SMC FB and SMC TF algorithms provide uniformly good approximations of marginal smoothing distributions contrary to direct method. In terms of MSE, only fast implementations of SMC FB/TF provide a gain in terms of MSE.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

78 / 136

Summary

SMC smoothing techniques allow us to solve the degeneracy problem. SMC xed-lag smoothing is the simplest one but has non-vanishing bias di cult to quantify. SMC FB and SMC TF algorithms provide uniformly good approximations of marginal smoothing distributions contrary to direct method. In terms of MSE, only fast implementations of SMC FB/TF provide a gain in terms of MSE. For direct implementation SMC FB/TF, MSE is of the same order but SMC FB/TF is bias dominated and direct SMC is variance dominated.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

78 / 136

ML Parameter Estimation in State-Space Models

In most scenarios of interest, the state-space model contains an unknown static parameter 2 so that X1 (x1 ) and Xt j (Xt
1

= xt

1)

f ( xt j xt

1) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

79 / 136

ML Parameter Estimation in State-Space Models

In most scenarios of interest, the state-space model contains an unknown static parameter 2 so that X1 (x1 ) and Xt j (Xt
1

= xt

1)

f ( xt j xt

1) .

The observations fYt gt 1 are conditionally independent given fXt gt 1 and Yt j (Xt = xt ) g ( yt j xt ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

79 / 136

ML Parameter Estimation in State-Space Models

In most scenarios of interest, the state-space model contains an unknown static parameter 2 so that X1 (x1 ) and Xt j (Xt
1

= xt

1)

f ( xt j xt

1) .

The observations fYt gt 1 are conditionally independent given fXt gt 1 and Yt j (Xt = xt ) g ( yt j xt ) . In many applications, we actually only care about and would like to estimate it o-line or on-line.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

79 / 136

Examples
Stochastic Volatility model Xt Yt

= Xt

1

+ Vt , Vt

i.i.d.

= exp (Xt /2) Wt , Wt

i.i.d.

N (0, 1) N (0, 1)

where = , 2 , .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

80 / 136

Examples
Stochastic Volatility model Xt Yt

= Xt

1

+ Vt , Vt

i.i.d.

= exp (Xt /2) Wt , Wt

i.i.d.

N (0, 1) N (0, 1)

where = , 2 , . Biochemical Network model Pr Xt1+dt =xt1+1, Xt2+dt =xt2 xt1 , xt2 = xt1 dt + o (dt ) , Pr Xt1+dt =xt1 1, Xt2+dt =xt2+1 xt1 , xt2 = xt1 xt2 dt + o (dt ) , Pr Xt1+dt =xt1 , Xt2+dt =xt2 1 xt1 , xt2 = xt2 dt + o (dt ) , with
1 Yk = Xk T + Wk with Wk i.i.d.

N 0, 2
Sept. 2012 80 / 136

where = (, , ) .
A. Doucet (MLSS Sept. 2012)

Likelihood Function Estimation
Let y1:T being given, the log-(marginal) likelihood is given by

`( ) = log p (y1:T ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

81 / 136

Likelihood Function Estimation
Let y1:T being given, the log-(marginal) likelihood is given by

`( ) = log p (y1:T ) .
For any 2 , one can estimate `( ) using standard SMC. methods, variance O (T /N ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

81 / 136

Likelihood Function Estimation
Let y1:T being given, the log-(marginal) likelihood is given by

`( ) = log p (y1:T ) .
For any 2 , one can estimate `( ) using standard SMC. methods, variance O (T /N ) . Direct maximization of `( ) di cult as SMC estimate b ) is not a `( smooth function of even for xed random seed.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

81 / 136

Likelihood Function Estimation
Let y1:T being given, the log-(marginal) likelihood is given by

`( ) = log p (y1:T ) .
For any 2 , one can estimate `( ) using standard SMC. methods, variance O (T /N ) . Direct maximization of `( ) di cult as SMC estimate b ) is not a `( smooth function of even for xed random seed. For dim (Xt ) = 1, we can obtain smooth estimate of log-likelihood function by using a smoothed resampling step (e.g. Pitt, 2002-2011); i.e. piecewise linear approximation of Pr ( Xt < x j y1:t ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

81 / 136

Likelihood Function Estimation
Let y1:T being given, the log-(marginal) likelihood is given by

`( ) = log p (y1:T ) .
For any 2 , one can estimate `( ) using standard SMC. methods, variance O (T /N ) . Direct maximization of `( ) di cult as SMC estimate b ) is not a `( smooth function of even for xed random seed. For dim (Xt ) = 1, we can obtain smooth estimate of log-likelihood function by using a smoothed resampling step (e.g. Pitt, 2002-2011); i.e. piecewise linear approximation of Pr ( Xt < x j y1:t ) . For dim (Xt ) > 1, we can obtain estimates of `( ) highly positively correlated for neigbouring values in (e.g. Lee, 2008).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

81 / 136

Gradient Ascent
To maximise `( ) w.r.t , use at iteration k + 1 k +1 = k + k r`( )j = k where r`( )j = k is the so-called score vector.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

82 / 136

Gradient Ascent
To maximise `( ) w.r.t , use at iteration k + 1 k +1 = k + k r`( )j = k

r`( )j =k can be estimated using nite dierences but more e ciently using Fisher identity (e.g. Capp et al., 2005) s r`( ) =
where
Z

where r`( )j = k is the so-called score vector.

r log p (x1:T , y1:T ) p ( x1:T j y1:T ) dx1:T

r log p (x1:T , y1:T ) = r log (x1 ) + T=2 r log f ( xt j xt 1 ) + T=1 r log g ( yt j xt ) . t t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

82 / 136

Gradient Ascent
To maximise `( ) w.r.t , use at iteration k + 1 k +1 = k + k r`( )j = k

r`( )j =k can be estimated using nite dierences but more e ciently using Fisher identity (e.g. Capp et al., 2005) s r`( ) =
where
Z

where r`( )j = k is the so-called score vector.

r log p (x1:T , y1:T ) p ( x1:T j y1:T ) dx1:T

r log p (x1:T , y1:T ) = r log (x1 ) + T=2 r log f ( xt j xt 1 ) + T=1 r log g ( yt j xt ) . t t
An alternative is to use IPA (Coquelin, Deguest & Munos, 2009).
A. Doucet (MLSS Sept. 2012) Sept. 2012 82 / 136

Example: SV Model
Remember that Xt Yt
i.i.d.

= Xt

1

+ Vt , Vt

= exp (Xt /2) Wt , Wt

i.i.d.

N (0, 1) N (0, 1)

where we assume here that 2 , are known so that = .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

83 / 136

Example: SV Model
Remember that Xt Yt
i.i.d.

= Xt

1

+ Vt , Vt

= exp (Xt /2) Wt , Wt

i.i.d.

N (0, 1) N (0, 1)

where we assume here that 2 , are known so that = . In this scenario 1 1 log f ( xt j xt 1 ) = log 22 (xt xt 1 )2 , 2 2 2 xt2 1 xt 1 (xt xt 1 ) xt 1 xt r log f ( xt j xt 1 ) = = , 2 2 2 hence E T=2 Xt t 2
1 Xt

r`( ) =

y1:T

E T=2 Xt2 t 2

1

y1:T .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

83 / 136

Gradient Ascent using SMC
An obvious SMC approximation is given by

\ k +1 = k + k r`( ) \ where r`( )
= k

= k

is estimated by your favourite SMC smoothing

technique.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

84 / 136

Gradient Ascent using SMC
An obvious SMC approximation is given by

\ k +1 = k + k r`( ) \ where r`( )
= k

= k

is estimated by your favourite SMC smoothing

technique.

As r`( ) is a smoothed additive functional, all previously presented SMC methods and results do apply; see previous numerical results.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

84 / 136

Gradient Ascent using SMC
An obvious SMC approximation is given by

\ k +1 = k + k r`( ) \ where r`( )
= k

= k

is estimated by your favourite SMC smoothing

technique.

As r`( ) is a smoothed additive functional, all previously presented SMC methods and results do apply; see previous numerical results. Similarly, it is possible to estimate the observed information matrix r2 `( ) using SMC based on Louis identity (e.g. Capp et al., 2005) to implement a Newton-Raphson algorithm (Poyadjis, D. & Singh, 2010).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

84 / 136

ML Parameter Estimation using EM
The Expectation-Maximization (EM) algorithm is a celebrated alternative to gradient ascent technique.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

85 / 136

ML Parameter Estimation using EM
The Expectation-Maximization (EM) algorithm is a celebrated alternative to gradient ascent technique. To maximise `( ) w.r.t , the EM uses k +1 = arg max Q ( k , ). where Q ( k , ) = and we know that
Z

log p (x1:T , y1:T ) p k (x1:T jy1:T )dx1:T

`( k +1 )

`( k ).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

85 / 136

ML Parameter Estimation using EM
The Expectation-Maximization (EM) algorithm is a celebrated alternative to gradient ascent technique. To maximise `( ) w.r.t , the EM uses k +1 = arg max Q ( k , ). where Q ( k , ) = and we know that
Z

log p (x1:T , y1:T ) p k (x1:T jy1:T )dx1:T

`( k +1 ) `( k ). If p (x1:T , y1:T ) is in the exponential family then we have
k +1 = T where
T =
A. Doucet (MLSS Sept. 2012)

1

Tk

Z

t =2

(xt

T

1 , xt , yt )

!

p (x1:T jy1:T )dx1:T
Sept. 2012 85 / 136

Example: SV Model
Remember that Xt Yt
i.i.d.

= Xt

1

+ Vt , Vt

= exp (Xt /2) Wt , Wt

i.i.d.

N (0, 1) N (0, 1)

where we assume here that 2 , are known so that = .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

86 / 136

Example: SV Model
Remember that Xt Yt
i.i.d.

= Xt

1

+ Vt , Vt

= exp (Xt /2) Wt , Wt

i.i.d.

N (0, 1) N (0, 1)

where we assume here that 2 , are known so that = . In this scenario log f ( xt j xt
1)

= =

1 log 22 2 1 log 22 2 E k E k T=2 Xt t

1 (xt xt 1 )2 22 2 xt2 1 xt2 xt 1 xt + 2 2 2 2 2
1 Xt 1

so that k +1 = y1:T . y1:T
Sept. 2012 86 / 136

T=2 Xt2 t

A. Doucet (MLSS Sept. 2012)

EM using SMC

SMC approximation of the EM is direct.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

87 / 136

EM using SMC

SMC approximation of the EM is direct. As EM requires computing smoothed additive functionals R T = T=2 (xt 1 , xt , yt ) p (x1:T jy1:T )dx1:T , all previously t presented SMC smoothing methods and results do apply.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

87 / 136

EM using SMC

SMC approximation of the EM is direct. As EM requires computing smoothed additive functionals R T = T=2 (xt 1 , xt , yt ) p (x1:T jy1:T )dx1:T , all previously t presented SMC smoothing methods and results do apply.

There is obviously no more guarantee that `( k +1 ) `( k ) for nite N but many positive experimental results; e.g. (Schon, Wills & Ninness, 2011).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

87 / 136

ML Parameter Estimation using Online Gradient
In many applications, we would like to estimate the parameter on-line.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

88 / 136

ML Parameter Estimation using Online Gradient
In many applications, we would like to estimate the parameter on-line. Recursive maximum likelihood (Titterington, 1984; LeGland & Mevel, 1997) proceeds as follows t +1 = t + t r log p 1:t ( yt j y1:t
1)

where p 1:t ( yt j y1:t 1 ) is computed using k at time k and t t = , t 2 < . Under regularity conditions, this converges t towards a local maximum of the (average) log-likelihood.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

88 / 136

ML Parameter Estimation using Online Gradient
In many applications, we would like to estimate the parameter on-line. Recursive maximum likelihood (Titterington, 1984; LeGland & Mevel, 1997) proceeds as follows t +1 = t + t r log p 1:t ( yt j y1:t
1)

where p 1:t ( yt j y1:t 1 ) is computed using k at time k and t t = , t 2 < . Under regularity conditions, this converges t towards a local maximum of the (average) log-likelihood. Note that

r log p1:t ( yt j y1:t

1)

= r log p1:t (y1:t )

r log p1:t

1

(y1:t

1)

is given by the dierence of two pseudo-score vectors where R r log p1:t (y1:t ) := t =2 r log f ( xk j xk 1 )j k k
A. Doucet (MLSS Sept. 2012)

+ r log g ( yk j xk )jk p1:t ( x1:t j y1:t ) dx1:t .
Sept. 2012 88 / 136

ML Parameter Estimation using SMC Online Gradient
SMC approximation follows

\ t +1 = t + t r log p 1:t ( yt j y1:t
where

1)

\ r log p 1:t ( yt j y1:t

1)

\ = r log p 1:t (y1:t )

\ r log p 1:t

1

(y1:t

1)

is given by the dierence of SMC estimates of pseudo-score vectors (Poyadjis, D. & Singh, 2011).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

89 / 136

ML Parameter Estimation using SMC Online Gradient
SMC approximation follows

\ t +1 = t + t r log p 1:t ( yt j y1:t
where

1)

\ r log p 1:t ( yt j y1:t

1)

\ = r log p 1:t (y1:t )

\ r log p 1:t

1

(y1:t

1)

is given by the dierence of SMC estimates of pseudo-score vectors (Poyadjis, D. & Singh, 2011). \ Asymptotic variance of r log p 1:t ( yt j y1:t 1 ) is uniformly bounded for FB estimate (Del Moral, D. & Singh, 2011) whereas it increases linearly with t for direct SMC method.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

89 / 136

ML Parameter Estimation using SMC Online Gradient
SMC approximation follows

\ t +1 = t + t r log p 1:t ( yt j y1:t
where

1)

\ r log p 1:t ( yt j y1:t

1)

\ = r log p 1:t (y1:t )

\ r log p 1:t

1

(y1:t

1)

is given by the dierence of SMC estimates of pseudo-score vectors (Poyadjis, D. & Singh, 2011). \ Asymptotic variance of r log p 1:t ( yt j y1:t 1 ) is uniformly bounded for FB estimate (Del Moral, D. & Singh, 2011) whereas it increases linearly with t for direct SMC method. Major Problem: If we use FB, this is not an online algorithm anymore as it requires a backward pass of order O (t ) to approximate r log p1:t (y1:t ) ...
A. Doucet (MLSS Sept. 2012) Sept. 2012 89 / 136

Variance of the Gradient Estimate for Direct vs FB
140 120 100 80 60 40 20 0 1 5000 10000 15000 20000

Figure: Empirical variance of the gradient estimate for standard versus FB approximations (SV model)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

90 / 136

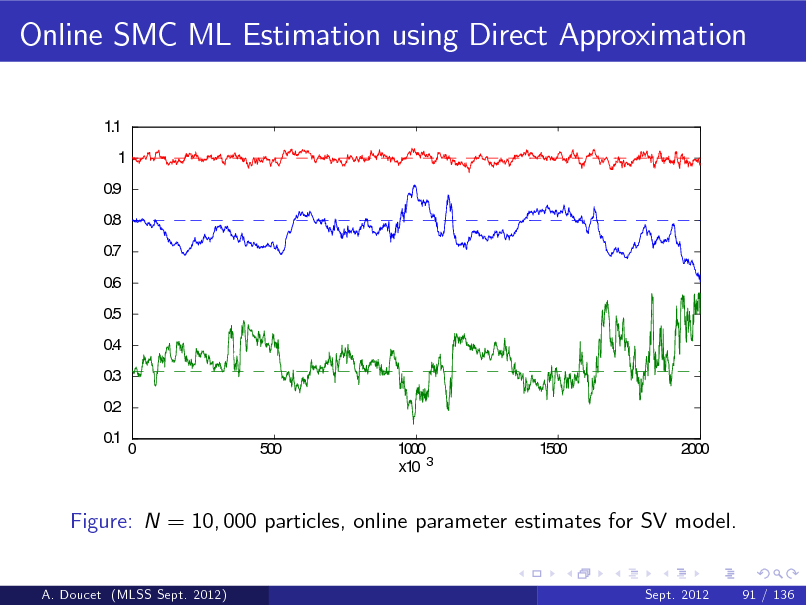
Online SMC ML Estimation using Direct Approximation
1.1 1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 500 1000 x10 3 1500 2000

Figure: N = 10, 000 particles, online parameter estimates for SV model.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

91 / 136

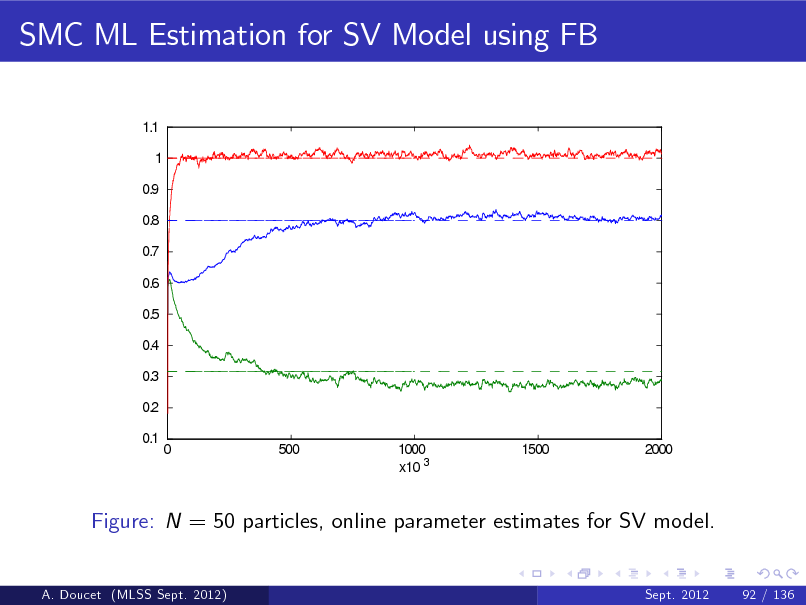
SMC ML Estimation for SV Model using FB
1.1 1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 500 1000 x10 3 1500 2000

Figure: N = 50 particles, online parameter estimates for SV model.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

92 / 136

Forward only Smoothing
For the time being, we do not have an online implementation as a backward pass of length t is required at time t.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

93 / 136

Forward only Smoothing
For the time being, we do not have an online implementation as a backward pass of length t is required at time t. It is possible to completely bypass the backward pass to compute using FB Z
t = t

t (x1:t ) p ( x1:t j y1:t ) dx1:t

where

t (x1:t ) =

k =1

(xk

t

1:k , yk )

using a dynamic programming trick for the backward Markov chain of transition densities fp ( xk j y1:k , xk +1 )g .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

93 / 136

Forward only Smoothing
For the time being, we do not have an online implementation as a backward pass of length t is required at time t. It is possible to completely bypass the backward pass to compute using FB Z
t = t

t (x1:t ) p ( x1:t j y1:t ) dx1:t

where

t (x1:t ) =

k =1

(xk

t

1:k , yk )

using a dynamic programming trick for the backward Markov chain of transition densities fp ( xk j y1:k , xk +1 )g . Let us introduce the value function Vt (xt ) := then
A. Doucet (MLSS Sept. 2012)

Z

t (x1:t ) p ( x1:t
Z

1 j y1:t 1 , xt ) dx1:t 1

t =

Vt (xt ) p ( xt j y1:t ) dxt .
Sept. 2012 93 / 136

Forward only Smoothing
Forward smoothing recursion Z h Vt 1 (xt 1 ) + (xt Vt (xt ) = i , yt ) p ( xt 1:t

1 j y1:t 1 , xt ) dxt 1

A. Doucet (MLSS Sept. 2012)

Sept. 2012

94 / 136

Forward only Smoothing
Forward smoothing recursion Z h Vt 1 (xt 1 ) + (xt Vt (xt ) = i , yt ) p ( xt 1:t

1 j y1:t 1 , xt ) dxt 1

Proof is trivial R VtR(xt ) = t (x1:t ) p ( x1:t 1 j y1:t 1 , xt ) dx1:t 1 = t 1 (x1:t 1 ) + (xt 1:t , yt ) p ( x1:t 2 j y1:t 2 , xt 1 ) p ( xt 1 j y1:t 1 , xt ) dx1:t R Z = ( t 1 (x1:t 1 ) p ( x1:t 2 j y1:t 2 , xt 1 ) dx1:t 2 {z } |
V t 1 (xt
1)

1

+ (xt

1:t , yt ))

p ( xt

1 j y1:t 1 , xt ) dxt 1

A. Doucet (MLSS Sept. 2012)

Sept. 2012

94 / 136

Forward only Smoothing
Forward smoothing recursion Z h Vt 1 (xt 1 ) + (xt Vt (xt ) = i , yt ) p ( xt 1:t

1 j y1:t 1 , xt ) dxt 1

Proof is trivial R VtR(xt ) = t (x1:t ) p ( x1:t 1 j y1:t 1 , xt ) dx1:t 1 = t 1 (x1:t 1 ) + (xt 1:t , yt ) p ( x1:t 2 j y1:t 2 , xt 1 ) p ( xt 1 j y1:t 1 , xt ) dx1:t R Z = ( t 1 (x1:t 1 ) p ( x1:t 2 j y1:t 2 , xt 1 ) dx1:t 2 {z } |
V t 1 (xt
1)

1

+ (xt

1:t , yt ))

p ( xt

1 j y1:t 1 , xt ) dxt 1

Appears implicitly in Elliott, Aggoun & Moore (1996), Ford (1998) and rediscovered a few times... Presentation follows here (Del Moral, D. & Singh, 2009).
A. Doucet (MLSS Sept. 2012) Sept. 2012 94 / 136

SMC Forward only Smoothing
At time t 1, we have p ( xt b n o (i ) b Vt 1 Xt 1 .
1 i N 1 j y1:t 1 )

=

1 N

N 1 X (i ) (xt i=
t 1

1)

and

A. Doucet (MLSS Sept. 2012)

Sept. 2012

95 / 136

SMC Forward only Smoothing
At time t 1, we have p ( xt b n o (i ) b Vt 1 Xt 1 .
1 i N 1 j y1:t 1 )

=

1 N

N 1 X (i ) (xt i=
t 1

1)

and

(i ) b Vt Xt =

At time t, compute p ( xt j y1:t ) = N 1 Wt X (i ) (xt ) and set b i=
t

(i )

=

Rh

N 1 f j=

b Vt

bt =

1 N

(i ) b . N 1 Vt Xt i=

(i ) b 1 ) + (xt 1:t , yt ) p xt 1 j y1:t 1 , Xt h i (i ) (j ) (j ) (j ) (i ) b X t jX t 1 V t 1 X t 1 + X t 1 ,X t ,yt
1

(xt

i

dxt

1

N 1 f X t jX t j=

(i )

(j ) 1

,

A. Doucet (MLSS Sept. 2012)

Sept. 2012

95 / 136

SMC Forward only Smoothing
At time t 1, we have p ( xt b n o (i ) b Vt 1 Xt 1 .
1 i N 1 j y1:t 1 )

=

1 N

N 1 X (i ) (xt i=
t 1

1)

and

(i ) b Vt Xt =

At time t, compute p ( xt j y1:t ) = N 1 Wt X (i ) (xt ) and set b i=
t

(i )

=

Rh

N 1 f j=

b Vt

bt =

1 N

This estimate is exactly the same as the SMC FB estimate, computational complexity O N 2 .
Sept. 2012 95 / 136

(i ) b . N 1 Vt Xt i=

(i ) b 1 ) + (xt 1:t , yt ) p xt 1 j y1:t 1 , Xt h i (i ) (j ) (j ) (j ) (i ) b X t jX t 1 V t 1 X t 1 + X t 1 ,X t ,yt
1

(xt

i

dxt

1

N 1 f X t jX t j=

(i )

(j ) 1

,

A. Doucet (MLSS Sept. 2012)

ML Parameter Estimation using SMC Online Gradient
At time t n o (i ) b 1, we have p 1:t 1 ( xt 1 j y1:t 1 ), Vt 1:t 1 Xt 1 and b 1 R 1:t 1 \p b r log 1:t 1 (y1:t 1 ) = Vt 1 (xt 1 ) p1:t 1 ( xt 1 j y1:t 1 ) dxt 1 b and obtained t .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

96 / 136

ML Parameter Estimation using SMC Online Gradient
n o (i ) b 1, we have p 1:t 1 ( xt 1 j y1:t 1 ), Vt 1:t 1 Xt 1 and b 1 R 1:t 1 \p b r log 1:t 1 (y1:t 1 ) = Vt 1 (xt 1 ) p1:t 1 ( xt 1 j y1:t 1 ) dxt 1 b and obtained t . At time t, use SMC to compute p 1:t ( xt j y1:t ) and b i R h 1:t 1 (i ) (i ) b Xt = Vt 1 (xt 1 ) + (xt 1:t , yt ) p 1:t xt 1 j y1:t 1 , Xt b dxt At time t

b Vt 1:t

1

(xt

1:t , yt )

= r log f ( xt j xt

1 )j t

+ r log g ( yt j xt )jt
Z

and

\ r log p 1:t (y1:t ) =

b b Vt 1:t (xt ) p 1:t ( xt j y1:t ) dxt

A. Doucet (MLSS Sept. 2012)

Sept. 2012

96 / 136

ML Parameter Estimation using SMC Online Gradient
n o (i ) b 1, we have p 1:t 1 ( xt 1 j y1:t 1 ), Vt 1:t 1 Xt 1 and b 1 R 1:t 1 \p b r log 1:t 1 (y1:t 1 ) = Vt 1 (xt 1 ) p1:t 1 ( xt 1 j y1:t 1 ) dxt 1 b and obtained t . At time t, use SMC to compute p 1:t ( xt j y1:t ) and b i R h 1:t 1 (i ) (i ) b Xt = Vt 1 (xt 1 ) + (xt 1:t , yt ) p 1:t xt 1 j y1:t 1 , Xt b dxt At time t

b Vt 1:t

1

(xt

1:t , yt )

= r log f ( xt j xt

1 )j t

+ r log g ( yt j xt )jt
Z

and

\ r log p 1:t (y1:t ) =
Parameter update t +1 = t + t

b b Vt 1:t (xt ) p 1:t ( xt j y1:t ) dxt

\ r log p 1:t (y1:t )

\ r log p 1:t

1

(y1:t

1)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

96 / 136

Online ML Parameter Estimation through EM
Batch EM uses
Tk

=

Z

t =2

(xt
1 Tk

T

1:t , yt )

!

p k (x1:T jy1:T )dx1:T ,

k +1 = T

A. Doucet (MLSS Sept. 2012)

Sept. 2012

97 / 136

Online ML Parameter Estimation through EM
Batch EM uses
Tk

=

Z

t =2

(xt
1 Tk

T

1:t , yt )

!

p k (x1:T jy1:T )dx1:T ,

k +1 = T

Online EM uses R 1:t t +1 = t +1 (xt :t +1 , yt +1 ) p 1:t (xt , xt +1 jy1:t +1 )dxt :t +1 !
1:t then set t +1 = t +1

+ (1 R

t +1 ) t =1 k

l =k +2

t

(1

l )

k +1

(xk

1:k , yk ) p 1:t (xk 1 , xk jy1:t +1 )dxk 1:k

t 2 t

< ; e.g. t = t

with 0.5 <

for ft gt

1

satisfying t t = and 1.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

97 / 136

Online ML Parameter Estimation through EM
Batch EM uses
Tk

=

Z

t =2

(xt
1 Tk

T

1:t , yt )

!

p k (x1:T jy1:T )dx1:T ,

k +1 = T

Online EM uses R 1:t t +1 = t +1 (xt :t +1 , yt +1 ) p 1:t (xt , xt +1 jy1:t +1 )dxt :t +1 !
1:t then set t +1 = t +1

+ (1 R

t +1 ) t =1 k

l =k +2

t

(1

l )

k +1

(xk

1:k , yk ) p 1:t (xk 1 , xk jy1:t +1 )dxk 1:k

< ; e.g. t = t with 0.5 < 1. Under regularity conditions, this converges towards a local maximum of the (average) log-likelihood (well not yet proven for HMM)
t 2 t

A. Doucet (MLSS Sept. 2012) Sept. 2012 97 / 136

for ft gt

1

satisfying t t = and

Online ML Parameter Estimation through SMC EM
n b Vt 1:t 1
(i ) 1

At time t 1, we have p 1:t b obtained t .

1

( xt

1 j y1:t 1 ),

1

Xt

o

and

A. Doucet (MLSS Sept. 2012)

Sept. 2012

98 / 136

Online ML Parameter Estimation through SMC EM
n b Vt 1:t 1
(i ) 1

At time t, use SMC to compute p 1:t ( xt 1 j y1:t 1 ) and b i Rh (i ) b b Vt 1:t Xt = (1 t ) Vt1:t 1 (xt 1 ) + t (xt 1:t , yt ) 1
t 1:t

At time t 1, we have p 1:t b obtained t .

1

( xt

1 j y1:t 1 ),

1

Xt

o

and

=

R

b Vt 1:t (xt ) p 1:t ( xt j y1:t ) dxt b

p 1:t b

xt

(i ) 1 j y1:t 1 , Xt

dxt

1,

A. Doucet (MLSS Sept. 2012)

Sept. 2012

98 / 136

Online ML Parameter Estimation through SMC EM
n b Vt 1:t 1
(i ) 1

At time t, use SMC to compute p 1:t ( xt 1 j y1:t 1 ) and b i Rh (i ) b b Vt 1:t Xt = (1 t ) Vt1:t 1 (xt 1 ) + t (xt 1:t , yt ) 1
t 1:t

At time t 1, we have p 1:t b obtained t .

1

( xt

1 j y1:t 1 ),

1

Xt

o

and

=

Parameter update

R

b Vt 1:t (xt ) p 1:t ( xt j y1:t ) dxt b

p 1:t b

xt

(i ) 1 j y1:t 1 , Xt

dxt

1,

t +1 = t 1:t

A. Doucet (MLSS Sept. 2012)

Sept. 2012

98 / 136

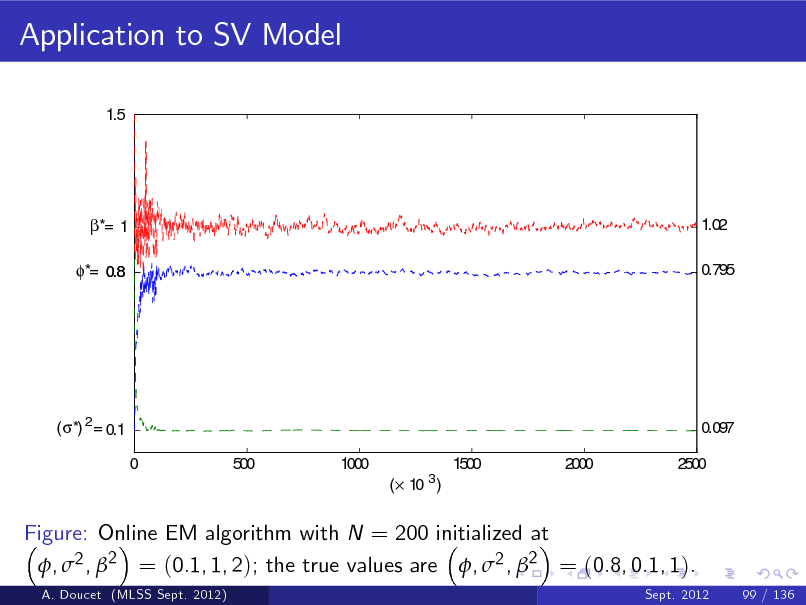
Application to SV Model
1.5

*= 1 *= 0.8

1.02 0.795

(*) 2= 0.1 0 500 1000 ( 10 3) 1500 2000

0.097 2500

Figure: Online EM algorithm with N = 200 initialized at , 2 , 2 = (0.1, 1, 2); the true values are , 2 , 2 = (0.8, 0.1, 1).
A. Doucet (MLSS Sept. 2012) Sept. 2012 99 / 136

Direct SMC vs Forward Smoothing for Online EM

For online gradient techniques, forward smoothing is stable contrary to the direct method.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

100 / 136

Direct SMC vs Forward Smoothing for Online EM

For online gradient techniques, forward smoothing is stable contrary to the direct method. Structure of online EM is signicantly dierent.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

100 / 136

Direct SMC vs Forward Smoothing for Online EM

For online gradient techniques, forward smoothing is stable contrary to the direct method. Structure of online EM is signicantly dierent. We have seen previously that the MSE for smoothed additive functionals is of the same order for direct and FB estimates.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

100 / 136

Direct SMC vs Forward Smoothing for Online EM

For online gradient techniques, forward smoothing is stable contrary to the direct method. Structure of online EM is signicantly dierent. We have seen previously that the MSE for smoothed additive functionals is of the same order for direct and FB estimates. Direct method is variance dominated, FB is bias dominated.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

100 / 136

Direct SMC vs Forward Smoothing for Online EM

For online gradient techniques, forward smoothing is stable contrary to the direct method. Structure of online EM is signicantly dierent. We have seen previously that the MSE for smoothed additive functionals is of the same order for direct and FB estimates. Direct method is variance dominated, FB is bias dominated. We compare experimentally both methods on a simple linear Gaussian model over 100 runs.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

100 / 136

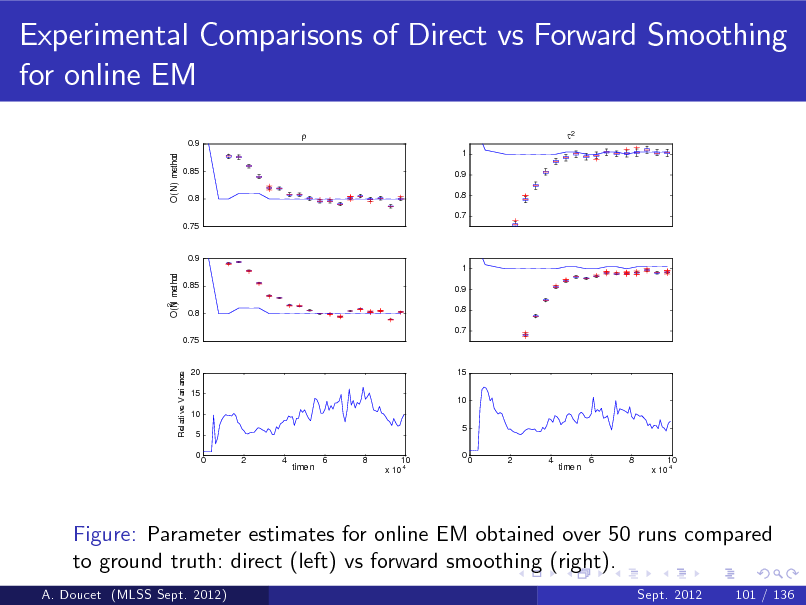
Experimental Comparisons of Direct vs Forward Smoothing for online EM
0.9
O(N) method

1

2

0.85 0.8 0.75

0.9 0.8 0.7

0.9
O(N met hod )

1 0.85 0.8 0.75 0.9 0.8 0.7

2

Rel at i ve Vari ance

20 15 10 5 0 0 2 4 6 8 10 x 10 4

15 10 5 0

time n

0

2

4

time n

6

8

10 x 10 4

Figure: Parameter estimates for online EM obtained over 50 runs compared to ground truth: direct (left) vs forward smoothing (right).
A. Doucet (MLSS Sept. 2012) Sept. 2012 101 / 136

Summary

SMC smoothing techniques can be used to perform o-line and on-line ML parameter estimation.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

102 / 136

Summary

SMC smoothing techniques can be used to perform o-line and on-line ML parameter estimation. FB estimates for smoothed additive functionals can be computed using a forward only procedure.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

102 / 136

Summary

SMC smoothing techniques can be used to perform o-line and on-line ML parameter estimation. FB estimates for smoothed additive functionals can be computed using a forward only procedure. Forward smoothing allows us to implement a degeneracy free on-line gradient ascent algorithm.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

102 / 136

Summary

SMC smoothing techniques can be used to perform o-line and on-line ML parameter estimation. FB estimates for smoothed additive functionals can be computed using a forward only procedure. Forward smoothing allows us to implement a degeneracy free on-line gradient ascent algorithm. For on-line EM, forward smoothing and direct methods have both pros and cons with no clear winner.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

102 / 136

Summary

SMC smoothing techniques can be used to perform o-line and on-line ML parameter estimation. FB estimates for smoothed additive functionals can be computed using a forward only procedure. Forward smoothing allows us to implement a degeneracy free on-line gradient ascent algorithm. For on-line EM, forward smoothing and direct methods have both pros and cons with no clear winner. Bias reduction approaches are currently under study.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

102 / 136

Bayesian Parameter Inference in State-Space Models
Assume we have Xt j (Xt

= xt 1 ) Yt j (Xt = xt )
1

f ( xt j xt

1) ,

g ( yt j xt ) ,

where is an unknown static parameter with prior p ( ).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

103 / 136

Bayesian Parameter Inference in State-Space Models
Assume we have Xt j (Xt

= xt 1 ) Yt j (Xt = xt )
1

f ( xt j xt

1) ,

g ( yt j xt ) ,

where is an unknown static parameter with prior p ( ). Given data y1:t , inference relies on p ( , x1:t j y1:t ) = p ( j y1:t ) p ( x1:t j y1:t ) where p ( j y1:t ) p (y1:t ) p ( ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

103 / 136

Bayesian Parameter Inference in State-Space Models
Assume we have Xt j (Xt

= xt 1 ) Yt j (Xt = xt )
1

f ( xt j xt

1) ,

g ( yt j xt ) ,

where is an unknown static parameter with prior p ( ). Given data y1:t , inference relies on p ( , x1:t j y1:t ) = p ( j y1:t ) p ( x1:t j y1:t ) where SMC methods apply as it is a standard model with extended state Zt = (Xt , t ) where f ( zt j zt
1)

p ( j y1:t ) p (y1:t ) p ( ) .

=

practical problems
A. Doucet (MLSS Sept. 2012) Sept. 2012 103 / 136

1 ( t ) | t {z }

f t ( xt j xt

1) ,

g ( yt j zt ) = g t ( yt j xt ) .

Cautionary Warning
2 For xed , V [p (y1:t )] /p (y1:t ) is in O (t/N ). b

A. Doucet (MLSS Sept. 2012)

Sept. 2012

104 / 136

Cautionary Warning
2 For xed , V [p (y1:t )] /p (y1:t ) is in O (t/N ). b

In a Bayesian context, the problem is even more complex as p ( j y1:t ) p (y1:t ) p ( ) and we have t = for all t so the latent process does not enjoy mixing properties.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

104 / 136

Cautionary Warning
2 For xed , V [p (y1:t )] /p (y1:t ) is in O (t/N ). b

In a Bayesian context, the problem is even more complex as p ( j y1:t ) p (y1:t ) p ( ) and we have t = for all t so the latent process does not enjoy mixing properties. A seemingly attractive idea consists of using MCMC steps on ; e.g. (Andrieu, De Freitas & D.,1999; Fearnhead, 2002; Gilks & Berzuini 2001; Storvik, 2002; Carvalho et al., 2010) so as to introduce some noise on the component of the state.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

104 / 136

Cautionary Warning
2 For xed , V [p (y1:t )] /p (y1:t ) is in O (t/N ). b

In a Bayesian context, the problem is even more complex as p ( j y1:t ) p (y1:t ) p ( ) and we have t = for all t so the latent process does not enjoy mixing properties. A seemingly attractive idea consists of using MCMC steps on ; e.g. (Andrieu, De Freitas & D.,1999; Fearnhead, 2002; Gilks & Berzuini 2001; Storvik, 2002; Carvalho et al., 2010) so as to introduce some noise on the component of the state. When p ( j y1:t , x1:t ) = p ( j st (x1:t , y1:t )) where st (x1:t , y1:t ) is a xed-dimensional of su cient statistics, the algorithm is particularly elegant but still implicitly relies on SMC approximation of p ( x1:t j y1:t ) so degeneracy will creep in.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

104 / 136

Cautionary Warning
2 For xed , V [p (y1:t )] /p (y1:t ) is in O (t/N ). b

In a Bayesian context, the problem is even more complex as p ( j y1:t ) p (y1:t ) p ( ) and we have t = for all t so the latent process does not enjoy mixing properties. A seemingly attractive idea consists of using MCMC steps on ; e.g. (Andrieu, De Freitas & D.,1999; Fearnhead, 2002; Gilks & Berzuini 2001; Storvik, 2002; Carvalho et al., 2010) so as to introduce some noise on the component of the state. When p ( j y1:t , x1:t ) = p ( j st (x1:t , y1:t )) where st (x1:t , y1:t ) is a xed-dimensional of su cient statistics, the algorithm is particularly elegant but still implicitly relies on SMC approximation of p ( x1:t j y1:t ) so degeneracy will creep in. As dim (Zt ) = dim (Xt ) + dim ( ), such methods are not recommended for high-dimensional , especially with vague priors.
Sept. 2012

A. Doucet (MLSS Sept. 2012)

104 / 136

SMC with MCMC Step for Parameter Estimation
Given at time t p ( , x1:t b 1, the approximation
1 j y1:t 1 )

=

1 N

i =1

N

t

(i )

(i ) 1 ,X 1:t 1

(, x1:t

1) ,

we update the approximation as follows at time t.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

105 / 136

SMC with MCMC Step for Parameter Estimation
Given at time t p ( , x1:t b 1, the approximation
1 j y1:t 1 )

=

1 N

i =1

N

t

(i )

(i ) 1 ,X 1:t 1

(, x1:t

1) ,

we update the approximation as follows at time t. (i ) (i ) e ( i ) f (i ) e (i ) e (i ) Sample Xt j Xt 1 , set X1:t = X1:t 1 , Xt
t 1

and

Wt

p ( , x1:t j y1:t ) = N 1 Wt e i=
(i )

(i )

t

(i )

g (i )

t 1

e (i ) . yt j Xt

e (i ) 1 ,X 1:t

(, x1:t ) ,

A. Doucet (MLSS Sept. 2012)

Sept. 2012

105 / 136

SMC with MCMC Step for Parameter Estimation
Given at time t p ( , x1:t b 1, the approximation
1 j y1:t 1 )

=

1 N

i =1

N

t

(i )

(i ) 1 ,X 1:t 1

(, x1:t

1) ,

we update the approximation as follows at time t. (i ) (i ) e ( i ) f (i ) e (i ) e (i ) Sample Xt j Xt 1 , set X1:t = X1:t 1 , Xt
t 1

and

Wt Resample X1:t

p ( , x1:t j y1:t ) = N 1 Wt e i=
(i )

(i )

t

(i )

g (i )

t 1

(i )

A. Doucet (MLSS Sept. 2012)

obtain p ( , x1:t j y1:t ) = b

p ( x1:t j y1:t ) then sample t e
1 N

e (i ) . yt j Xt N 1 i=

e (i ) 1 ,X 1:t

(, x1:t ) ,

(i )

t ,X 1:t

(i )

(i )

(, x1:t ).

p j y1:t , X1:t

(i )

to

Sept. 2012

105 / 136

A Toy Example
Linear Gaussian state-space model Xt = Xt
1

+ V Vt , Vt

i.i.d.

Yt = Xt + W Wt , Wt

i.i.d.

N (0, 1)

N (0, 1) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

106 / 136

A Toy Example
Linear Gaussian state-space model Xt = Xt
1

+ V Vt , Vt

i.i.d.

Yt = Xt + W Wt , Wt We set p ( ) 1(
1,1 )

i.i.d.

N (0, 1)

N (0, 1) .

( ) so
1,1 )

p ( j y1:t , x1:t ) N ; mt , 2 1( t where 2 = S2,t1 , mt = S2,t1 S1,t t with S1,t =

( )

k =2

xk

t

1 xk ,

S2,t =

k =2

xk2

t

1

A. Doucet (MLSS Sept. 2012)

Sept. 2012

106 / 136

SMC with MCMC Step for Parameter Estimation
At time t p ( , xt b 1, t
1 , st

(i )

(i ) (i ) 1 , Xt 1 , St 1
1) =

we have

1 j y1:t

1 N

i =1

N

t

(i )

(i ) (i ) 1 ,X t 1 ,S t 1

(, xt

1 , st 1 ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

107 / 136

SMC with MCMC Step for Parameter Estimation
At time t p ( , xt b 1, t
1 , st

(i )

(i ) (i ) 1 , Xt 1 , St 1
1) =

we have

1 j y1:t

1 N

i =1

N

t

(i )

(i ) (i ) 1 ,X t 1 ,S t 1

(, xt

1 , st 1 ) .

e (i ) Sample Xt
(i ) e (i ) S2,t = S2,t

f (i )
1

t 1

+ Xt

(i ) 2 , 1

j Xt

(i ) 1

Wt

(i )

(i ) e (i ) , set S1,t = S1,t

1

+ Xt

g (i )
(i )

t 1

p ( , xt , st j y1:t ) = e

i =1

Wt

N

e yt j Xt

(i )

and

(i ) e (i ) 1 Xt ,

t

(i )

e (i ) e (i ) 1 ,X t ,S t

(, xt , st ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

107 / 136

SMC with MCMC Step for Parameter Estimation
At time t p ( , xt b 1, t
1 , st

(i )

(i ) (i ) 1 , Xt 1 , St 1
1) =

we have

1 j y1:t

1 N

i =1

N

t

(i )

(i ) (i ) 1 ,X t 1 ,S t 1

(, xt

1 , st 1 ) .

e (i ) Sample Xt
(i ) e (i ) S2,t = S2,t

f (i )
1

t 1

+ Xt

(i ) 2 , 1

j Xt

(i ) 1

Wt

(i )

(i ) e (i ) , set S1,t = S1,t

1

+ Xt

g (i )
(i )

t 1

Resample Xt , St t
(i )

p ( , xt , st j y1:t ) = e
(i ) (i )

i =1

Wt
(i )

N

e yt j Xt

(i )

and

(i ) e (i ) 1 Xt ,

t

(i )

N

; S2,t

(i )
1 N

1

S1,t , S2,t
(i )

p ( xt , st j y1:t ) then sample e
(i )
1

e (i ) e (i ) 1 ,X t ,S t

(, xt , st ) .

1(

1,1 )

( ) to obtain

A. Doucet (MLSS Sept. 2012)

p ( , xt , st j y1:t ) = b

N 1 i=

t ,X t ,S t

(i )

(i )

(, xt , st ).
Sept. 2012 107 / 136

Illustration of the Degeneracy Problem
0 .7 0 .6 0 .5 0 .4 0 .3 0 .2 0 .1 0

0

50 0

10 00

10 50

20 00

20 50

30 00

30 50

40 00

40 50

50 00

SMC estimate of E [ j y1:t ], as t increases the degeneracy creeps in.
A. Doucet (MLSS Sept. 2012) Sept. 2012 108 / 136

Another Toy Example

Linear Gaussian state-space model Xt = Xt
1

+ Vt , Vt

i.i.d. i.i.d.

N (0, 1)

Yt = Xt + Wt , Wt

N (0, 1) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

109 / 136

Another Toy Example

Linear Gaussian state-space model Xt = Xt
1

+ Vt , Vt

i.i.d. i.i.d.

N (0, 1)

Yt = Xt + Wt , Wt We set

N (0, 1) .

U(

1,1 )

and 2

IG (1, 1).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

109 / 136

Another Toy Example

Linear Gaussian state-space model Xt = Xt
1

+ Vt , Vt

i.i.d. i.i.d.

N (0, 1)

Yt = Xt + Wt , Wt We set

N (0, 1) .

U( 1,1 ) and 2 IG (1, 1). We use particle lter with perfect adaptation and Gibbs moves with N = 10000; particle learning (Andrieu, D. & De Freitas, 1999; Carvalho et al., 2010)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

109 / 136

Another Toy Example

Linear Gaussian state-space model Xt = Xt
1

+ Vt , Vt

i.i.d. i.i.d.

N (0, 1)

Yt = Xt + Wt , Wt We set

N (0, 1) .

U( 1,1 ) and 2 IG (1, 1). We use particle lter with perfect adaptation and Gibbs moves with N = 10000; particle learning (Andrieu, D. & De Freitas, 1999; Carvalho et al., 2010) We compare to the ground truth obtained using Kalman lter on states and grid on parameters.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

109 / 136

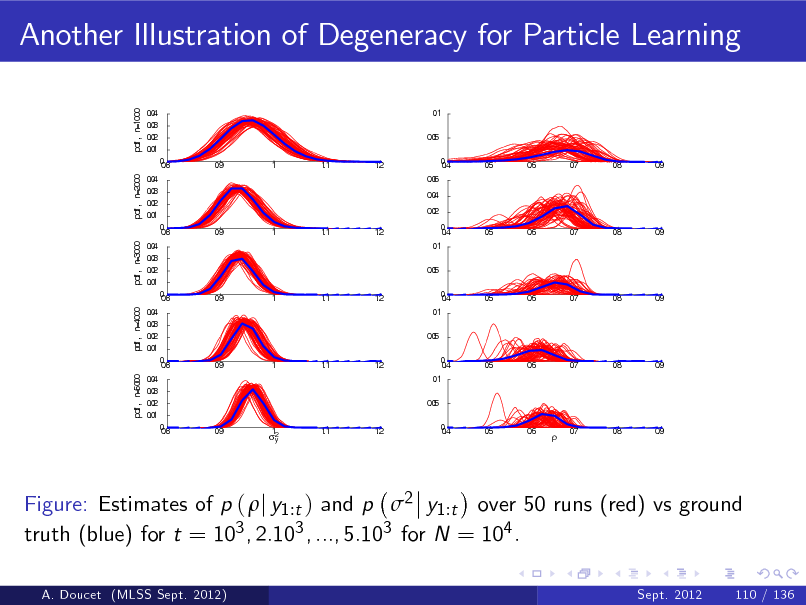
Another Illustration of Degeneracy for Particle Learning
pdf , n=1000

04 .0 03 .0 02 .0 01 .0 0.8 0 0 .9 1 1 .1 1 .2 04 .0 03 .0 02 .0 01 .0 0.8 0 0 .9 1 1 .1 1 .2 04 .0 03 .0 02 .0 01 .0 0.8 0 0 .9 1 1 .1 1 .2 04 .0 03 .0 02 .0 01 .0 0.8 0 0 .9 1 1 .1 1 .2 04 .0 03 .0 02 .0 01 .0 0.8 0 0 .9 1 2 y 1 .1 1 .2

0 .1 05 .0 0.4 0 06 .0 04 .0 02 .0 0.4 0 0 .1 05 .0 0.4 0 0 .1 05 .0 0.4 0 0 .1 05 .0 0.4 0 0 .5 0 .6 0 .7 0 .8 0 .9 0 .5 0 .6 0 .7 0 .8 0 .9 0 .5 0 .6 0 .7 0 .8 0 .9 0 .5 0 .6 0 .7 0 .8 0 .9 0 .5 0 .6 0 .7 0 .8 0 .9

pdf , n=5000

pdf , n=4000

pdf , n=3000

pdf , n=2000

Figure: Estimates of p ( j y1 :t ) and p 2 y1 :t over 50 runs (red) vs ground truth (blue) for t = 103 , 2.103 , ..., 5.103 for N = 104 .
A. Doucet (MLSS Sept. 2012) Sept. 2012 110 / 136

Online Bayesian Parameter Estimation

All proposed procedures for online Bayesian parameter estimation are decient. Some articial dynamics can be introduced but then we do not approximate fp ( , x1:t j y1:t )gt 1 ; e.g. (Liu & West, 2001; Flury & Shephard, 2010). Methods based on MCMC steps are elegant but do suer from the degeneracy problem and provide unreliable approximations.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

111 / 136

O- ine Bayesian Parameter Estimation

Given a collection of observations y1:T := (y1 , ..., yT ), T being xed, inference relies on the posterior density p ( , x1:T j y1:T ) = p ( j y1:T ) p ( x1:T j y1:T ) p (, x1:T , y1:T ) where p (, x1:T , y1:T ) p ( ) (x1 ) f ( xt j xt
t =2 T 1)

t =1

g ( yt j xt )

T

.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

112 / 136

O- ine Bayesian Parameter Estimation

Given a collection of observations y1:T := (y1 , ..., yT ), T being xed, inference relies on the posterior density p ( , x1:T j y1:T ) = p ( j y1:T ) p ( x1:T j y1:T ) p (, x1:T , y1:T ) where p (, x1:T , y1:T ) p ( ) (x1 ) f ( xt j xt
t =2 T 1)

t =1

g ( yt j xt )

T

.

We show how to address this problem using particle MCMC (Andrieu, D. & Holenstein, JRSS B, 2010).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

112 / 136

Common MCMC Approaches and Limitations

MCMC Idea: Simulate an ergodic Markov chain f (i ) , X1:T (i )gi of invariant distribution p ( , x1:T j y1:T )... innite number of possibilities.

0

A. Doucet (MLSS Sept. 2012)

Sept. 2012

113 / 136

Common MCMC Approaches and Limitations

MCMC Idea: Simulate an ergodic Markov chain f (i ) , X1:T (i )gi of invariant distribution p ( , x1:T j y1:T )... innite number of possibilities. Typical strategies consists of updating iteratively X1:T conditional upon then conditional upon X1:T .

0

A. Doucet (MLSS Sept. 2012)

Sept. 2012

113 / 136

Common MCMC Approaches and Limitations

MCMC Idea: Simulate an ergodic Markov chain f (i ) , X1:T (i )gi of invariant distribution p ( , x1:T j y1:T )... innite number of possibilities. Typical strategies consists of updating iteratively X1:T conditional upon then conditional upon X1:T . To update X1:T conditional upon , use MCMC kernels updating subblocks according to p ( xt :t +K 1 j yt :t +K 1 , xt 1 , xt +K ).

0

A. Doucet (MLSS Sept. 2012)

Sept. 2012

113 / 136

Common MCMC Approaches and Limitations

MCMC Idea: Simulate an ergodic Markov chain f (i ) , X1:T (i )gi of invariant distribution p ( , x1:T j y1:T )... innite number of possibilities. Typical strategies consists of updating iteratively X1:T conditional upon then conditional upon X1:T . To update X1:T conditional upon , use MCMC kernels updating subblocks according to p ( xt :t +K 1 j yt :t +K 1 , xt 1 , xt +K ).

0

Standard MCMC algorithms are ine cient if and X1:T are strongly correlated.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

113 / 136

Common MCMC Approaches and Limitations

MCMC Idea: Simulate an ergodic Markov chain f (i ) , X1:T (i )gi of invariant distribution p ( , x1:T j y1:T )... innite number of possibilities. Typical strategies consists of updating iteratively X1:T conditional upon then conditional upon X1:T . To update X1:T conditional upon , use MCMC kernels updating subblocks according to p ( xt :t +K 1 j yt :t +K 1 , xt 1 , xt +K ).

0

Standard MCMC algorithms are ine cient if and X1:T are strongly correlated. Strategy impossible to implement when it is only possible to sample from the prior but impossible to evaluate it pointwise.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

113 / 136

Metropolis-Hastings (MH) Sampling
To bypass these problems, we want to update jointly and X1:T .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

114 / 136

Metropolis-Hastings (MH) Sampling
To bypass these problems, we want to update jointly and X1:T . Assume that the current state of our Markov chain is (, x1:T ), we propose to update simultaneously the parameter and the states using a proposal q ( ( , x1:T )j (, x1:T )) = q ( j ) q ( x1:T j y1:T ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

114 / 136

Metropolis-Hastings (MH) Sampling
To bypass these problems, we want to update jointly and X1:T . Assume that the current state of our Markov chain is (, x1:T ), we propose to update simultaneously the parameter and the states using a proposal q ( ( , x1:T )j (, x1:T )) = q ( j ) q ( x1:T j y1:T ) . The proposal ( , x1:T ) is accepted with MH acceptance probability 1^ p ( , x1:T j y1:T ) q ( (x1:T , )j (x1:T , )) p ( , x1:T j y1:T ) q (x1:T , ) (x1:T , )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

114 / 136

Metropolis-Hastings (MH) Sampling
To bypass these problems, we want to update jointly and X1:T . Assume that the current state of our Markov chain is (, x1:T ), we propose to update simultaneously the parameter and the states using a proposal q ( ( , x1:T )j (, x1:T )) = q ( j ) q ( x1:T j y1:T ) . The proposal ( , x1:T ) is accepted with MH acceptance probability 1^ p ( , x1:T j y1:T ) q ( (x1:T , )j (x1:T , )) p ( , x1:T j y1:T ) q (x1:T , ) (x1:T , )

Problem: Designing a proposal q ( x1:T j y1:T ) such that the acceptance probability is not extremely small is very di cult.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

114 / 136

Idealized Marginal MH Sampler

Consider the following so-called marginal Metropolis-Hastings (MH) algorithm which uses as a proposal q ( (x1:T , )j (x1:T , )) = q ( j ) p ( x1:T j y1:T ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

115 / 136

Idealized Marginal MH Sampler

Consider the following so-called marginal Metropolis-Hastings (MH) algorithm which uses as a proposal q ( (x1:T , )j (x1:T , )) = q ( j ) p ( x1:T j y1:T ) . The MH acceptance probability is 1^ p ( , x1:T j y1:T ) q ( (x1:T , )j (x1:T , )) p ( , x1:T j y1:T ) q (x1:T , ) (x1:T , )

= 1^

p (y1:T ) p ( ) q ( j ) p (y1:T ) p ( ) q ( j )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

115 / 136

Idealized Marginal MH Sampler

Consider the following so-called marginal Metropolis-Hastings (MH) algorithm which uses as a proposal q ( (x1:T , )j (x1:T , )) = q ( j ) p ( x1:T j y1:T ) . The MH acceptance probability is 1^ p ( , x1:T j y1:T ) q ( (x1:T , )j (x1:T , )) p ( , x1:T j y1:T ) q (x1:T , ) (x1:T , )

= 1^

p (y1:T ) p ( ) q ( j ) p (y1:T ) p ( ) q ( j )

In this MH algorithm, X1:T has been essentially integrated out.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

115 / 136

Implementation Issues

Problem 1: We do not know p (y1:T ) = analytically.

R

p (x1:T , y1:T ) dx1:T

A. Doucet (MLSS Sept. 2012)

Sept. 2012

116 / 136

Implementation Issues

Problem 1: We do not know p (y1:T ) = analytically.

Problem 2: We do not know how to sample from p ( x1:T j y1:T ) .

R

p (x1:T , y1:T ) dx1:T

A. Doucet (MLSS Sept. 2012)

Sept. 2012

116 / 136

Implementation Issues

Problem 1: We do not know p (y1:T ) = analytically.

Problem 2: We do not know how to sample from p ( x1:T j y1:T ) .

R

p (x1:T , y1:T ) dx1:T

Idea: Use SMC approximations of p ( x1:T j y1:T ) and p (y1:T ).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

116 / 136

Sequential Monte Carlo aka Particle Filters
Given , SMC methods provide approximations of p ( x1:T j y1:T ) and p (y1:T ).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

117 / 136

Sequential Monte Carlo aka Particle Filters
Given , SMC methods provide approximations of p ( x1:T j y1:T ) and p (y1:T ). At time T , we obtain the following approximation of the posterior of interest 1 N p ( x1:T j y1:T ) = b (k ) (x1:T ) N k X 1:T =1 and an approximation of p (y1:T ) is given by p (y1:T ) = p (y1 ) p ( yt j y1:t b b b
t =2 1) T 1)

=

t =1

T

1 N

k =1

N

g

(k ) yt j Xt

!

if we use f ( xt j xt

as a proposal.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

117 / 136

Reminder...
Under mixing assumptions, we have V [p (y1:T )] b 2 p (y1:T ) D T . N

A. Doucet (MLSS Sept. 2012)

Sept. 2012

118 / 136

Reminder...
Under mixing assumptions, we have V [p (y1:T )] b 2 p (y1:T ) D T . N

Under mixing assumptions, we also have
Z

so if I run an SMC method to obtain p ( x1:T j y1:T ) then b X1:T p ( x1:T j y1:T ), unconditionally X1:T b E [p ( j y1:T )]. b

b jE [p ( x1:T j y1:T )]

p ( x1:T j y1:T )j dx1:T

C

T N

A. Doucet (MLSS Sept. 2012)

Sept. 2012

118 / 136

Reminder...
Under mixing assumptions, we have V [p (y1:T )] b 2 p (y1:T ) D T . N

Under mixing assumptions, we also have
Z

so if I run an SMC method to obtain p ( x1:T j y1:T ) then b X1:T p ( x1:T j y1:T ), unconditionally X1:T b E [p ( j y1:T )]. b

b jE [p ( x1:T j y1:T )]

p ( x1:T j y1:T )j dx1:T

C

T N

Problem: We cannot compute analytically the particle lter proposal q ( x1:T j y1:T ) = E [p ( x1:T j y1:T )] as it involves an expectation w.r.t b all the variables appearing in the particle algorithm...
Sept. 2012 118 / 136

A. Doucet (MLSS Sept. 2012)

Idealized Marginal MH Sampler

At iteration i Sample q ( j (i 1)).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

119 / 136

Idealized Marginal MH Sampler

At iteration i Sample Sample X1:T q ( j (i 1)). p ( x1:T j y1:T ) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

119 / 136

Idealized Marginal MH Sampler

At iteration i Sample Sample X1:T q ( j (i 1)). p ( x1:T j y1:T ) . p (y1:T ) p ( ) q ( (i 1)j ) 1)) q ( j (i 1)) 1 ) (y1:T ) p ( (i 1),

With probability 1^

p (i

set (i ) = , X1:T (i ) = X1:T otherwise set (i ) = (i X1:T (i ) = X1:T (i 1) .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

119 / 136

Particle Marginal MH Sampler

At iteration i Sample q ( j (i 1)) and run an SMC algorithm to obtain p ( x1:T j y1:T ) and p (y1:T ). b b

A. Doucet (MLSS Sept. 2012)

Sept. 2012

120 / 136

Particle Marginal MH Sampler

At iteration i Sample q ( j (i 1)) and run an SMC algorithm to obtain p ( x1:T j y1:T ) and p (y1:T ). b b Sample X1:T p ( x1:T j y1:T ) . b

A. Doucet (MLSS Sept. 2012)

Sept. 2012

120 / 136

Particle Marginal MH Sampler

At iteration i Sample q ( j (i 1)) and run an SMC algorithm to obtain p ( x1:T j y1:T ) and p (y1:T ). b b Sample X1:T With probability 1^ p ( x1:T j y1:T ) . b p (y1:T ) p ( ) b q ( (i 1)j ) 1)) q ( j (i 1)) 1 ) (y1:T ) p ( (i

set (i ) = , X1:T (i ) = X1:T otherwise set (i ) = (i X1:T (i ) = X1:T (i 1) .

p (i b

1),

A. Doucet (MLSS Sept. 2012)

Sept. 2012

120 / 136

Validity of the Particle Marginal MH Sampler

Proposition. Assume that the idealizedmarginal MH sampler chain is ergodic then, under very weak assumptions, the PMMH sampler chain is ergodic and admits p ( , x1:T j y1:T ) whatever being N 1.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

121 / 136

Validity of the Particle Marginal MH Sampler

Proposition. Assume that the idealizedmarginal MH sampler chain is ergodic then, under very weak assumptions, the PMMH sampler chain is ergodic and admits p ( , x1:T j y1:T ) whatever being N 1. It is easy to show the simpler result that the PMMH admits p ( j y1:T ) as invariant distribution whatever being N 1.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

121 / 136

Validity of the Particle Marginal MH Sampler

Proposition. Assume that the idealizedmarginal MH sampler chain is ergodic then, under very weak assumptions, the PMMH sampler chain is ergodic and admits p ( , x1:T j y1:T ) whatever being N 1. It is easy to show the simpler result that the PMMH admits p ( j y1:T ) as invariant distribution whatever being N 1.
Z

Let U denote all the r.v. introduce to build the SMC estimate then write p (y1:T ) = p (y1:T , U ) and from unbiasedness b b p (y1:T , u ) q (u ) du = p (y1:T ) . b

A. Doucet (MLSS Sept. 2012)

Sept. 2012

121 / 136

An Incomplete But Trivial Proof
The PMMH targets the distribution e (, u ) p ( ) p (y1:T , u ) q (u ) b e ( ) = p ( j y1:T ).

which satises

A. Doucet (MLSS Sept. 2012)

Sept. 2012

122 / 136

An Incomplete But Trivial Proof
The PMMH targets the distribution e (, u ) p ( ) p (y1:T , u ) q (u ) b e ( ) = p ( j y1:T ).

which satises

The PMMH sampler uses as a proposal

q ( ( , u )j (, u )) = q ( j ) q (u ) and
e ( ,u ) q ( (,u )j( ,u )) e (,u ) q ( ( ,u )j(,u ))

=

p ( )p (y1:T ,u )q (u ) q ( j )q (u ) b p ( )p (y1:T ,u )q (u ) q ( j )q (u ) b b q 1:T ,u = p (())pp ((yy1:T ,u ) ) q ( j ) p b ( j )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

122 / 136

An Incomplete But Trivial Proof
The PMMH targets the distribution e (, u ) p ( ) p (y1:T , u ) q (u ) b e ( ) = p ( j y1:T ).

which satises

The PMMH sampler uses as a proposal

q ( ( , u )j (, u )) = q ( j ) q (u ) and
e ( ,u ) q ( (,u )j( ,u )) e (,u ) q ( ( ,u )j(,u ))

=

Trivial but deep result: if you plug any unbiased likelihood estimate within a MCMC scheme, you do not perturb the invariant distribution.
A. Doucet (MLSS Sept. 2012) Sept. 2012 122 / 136

p ( )p (y1:T ,u )q (u ) q ( j )q (u ) b p ( )p (y1:T ,u )q (u ) q ( j )q (u ) b b q 1:T ,u = p (())pp ((yy1:T ,u ) ) q ( j ) p b ( j )

Explicit Structure of the Target Distribution
Let rst consider the case where T = 1.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

123 / 136

Explicit Structure of the Target Distribution
Let rst consider the case where T = 1. Proposal distribution q e , k, x1
(1:N )

= q ( j )

m =1

N

x1

(m )

W1

(k )

|

q (u )

{z

}

A. Doucet (MLSS Sept. 2012)

Sept. 2012

123 / 136

Explicit Structure of the Target Distribution
Let rst consider the case where T = 1. Proposal distribution q e , k, x1
(1:N )

= q ( j )

m =1

N

x1

(m )

W1

(k )

Target distribution , k, x1
(1:N )

|

q (u )

{z

} x1
(m )

p ( )

1 N |

m =1

N

g y1 j x1
p (y 1 ) b

(m )

{z

}

m =1

N

W1

(k )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

123 / 136

Explicit Structure of the Target Distribution
Let rst consider the case where T = 1. Proposal distribution q e , k, x1
(1:N )

= q ( j )

m =1

N

x1

(m )

W1

(k )

Target distribution , k, x1
(1:N )

|

q (u )

{z

} x1
(m )

p ( )

We have already shown

1 N |

m =1

N

g y1 j x1
p (y 1 ) b

(m )

{z

}

m =1

N

W1

(k )

, k, x1 qN e

(1:N )

(1:N ) , k, x1

=

p ( ) p (y1 ) b q ( j ) p (y1 )
Sept. 2012 123 / 136

A. Doucet (MLSS Sept. 2012)

Explicit Structure of the Target Distribution
The target is given by
(1:N ) , k, x1

p ( )
(k )

m =1

N

g

(m ) y1 j x1

!
(m )

m =1

.

N

x1

(m )

W1

(k )

but W1

(k )

= g y1 j x1

/ N =1 g y1 j x1 m

A. Doucet (MLSS Sept. 2012)

Sept. 2012

124 / 136

Explicit Structure of the Target Distribution
The target is given by
(1:N ) , k, x1

p ( )
(k )

m =1

N

g

(m ) y1 j x1

!
(m )

m =1

.

N

x1

(m )

W1

(k )

but W1

(k )

Hence, we can actually rewrite the target as
N

= g y1 j x1

/ N =1 g y1 j x1 m p , x1
(k )

(1:N ) , k, x1

=

y1

N

m =1;m 6=k

N

x1

(m )

.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

124 / 136

Explicit Structure of the Target Distribution
The target is given by
(1:N ) , k, x1

p ( )
(k )

m =1

N

g

(m ) y1 j x1

!
(m )

m =1

.

N

x1

(m )

W1

(k )

but W1

(k )

Hence, we can actually rewrite the target as
N

= g y1 j x1

/ N =1 g y1 j x1 m p , x1
(k )

(1:N ) , k, x1

=

y1

N

m =1;m 6=k

N

x1

(m )

.

This shows that we are able to sample from p ( , x1 j y1 ) and not only its marginal p ( j y1 ) .
A. Doucet (MLSS Sept. 2012) Sept. 2012 124 / 136

Sampling from the Target Distribution

To sample from this target distribution

A. Doucet (MLSS Sept. 2012)

Sept. 2012

125 / 136

Sampling from the Target Distribution

To sample from this target distribution
Sample K from a uniform distribution on f1, ..., N g.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

125 / 136

Sampling from the Target Distribution

To sample from this target distribution
Sample , X1 from p ( , x1 j y1 ). (We do not know how to do this, this is why we use MCMC). Sample K from a uniform distribution on f1, ..., N g.
(K )

A. Doucet (MLSS Sept. 2012)

Sept. 2012

125 / 136

Sampling from the Target Distribution

To sample from this target distribution
Sample , X1 from p ( , x1 j y1 ). (We do not know how to do this, this is why we use MCMC). Sample K from a uniform distribution on f1, ..., N g.
(K )

Sample X1

(m )

(x1 ) for m 6= K .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

125 / 136

Explicit Structure of the Target Distribution

This construction can be extended to the case T > 1.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

126 / 136

Explicit Structure of the Target Distribution

This construction can be extended to the case T > 1. To sample from this target distribution

A. Doucet (MLSS Sept. 2012)

Sept. 2012

126 / 136

Explicit Structure of the Target Distribution

This construction can be extended to the case T > 1. To sample from this target distribution
Sample indexes from a uniform distribution on f1, ..., N gT corresponding to an ancestral line.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

126 / 136

Explicit Structure of the Target Distribution

This construction can be extended to the case T > 1. To sample from this target distribution
Sample indexes from a uniform distribution on f1, ..., N gT corresponding to an ancestral line. Sample and X1 :T for this ancestral line from p ( , x1 :T j y1 :T ). (We do not know how to do this, this is why we use MCMC).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

126 / 136

Explicit Structure of the Target Distribution

This construction can be extended to the case T > 1. To sample from this target distribution
Sample indexes from a uniform distribution on f1, ..., N gT corresponding to an ancestral line. Sample and X1 :T for this ancestral line from p ( , x1 :T j y1 :T ). (We do not know how to do this, this is why we use MCMC).

Run a conditional SMC algorithm compatible with X1:T and its ancestral lineage; see (Andrieu, D. & Holenstein, 2010).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

126 / 136

Conditional SMC

Figure: Example of N 1 = 4 ancestral lineages generated by a conditional SMC 2 2 algorithm for N = 5, T = 3 conditional upon X1 :3 and B1 :3
A. Doucet (MLSS Sept. 2012) Sept. 2012 127 / 136

Idealized Gibbs Sampler

To sample from p ( , x1:T j y1:T ), an MCMC strategy consists of using the following block Gibbs sampler. At iteration i

A. Doucet (MLSS Sept. 2012)

Sept. 2012

128 / 136

Idealized Gibbs Sampler

To sample from p ( , x1:T j y1:T ), an MCMC strategy consists of using the following block Gibbs sampler. At iteration i Sample X1:T (i ) p (i
1)

( x1:T j y1:T ).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

128 / 136

Idealized Gibbs Sampler

To sample from p ( , x1:T j y1:T ), an MCMC strategy consists of using the following block Gibbs sampler. At iteration i Sample X1:T (i ) Sample (i )

( x1:T j y1:T ). p ( j y1:T , X1:T (i )) .
p (i
1)

A. Doucet (MLSS Sept. 2012)

Sept. 2012

128 / 136

Idealized Gibbs Sampler

To sample from p ( , x1:T j y1:T ), an MCMC strategy consists of using the following block Gibbs sampler. At iteration i Sample X1:T (i ) Sample (i )

( x1:T j y1:T ). p ( j y1:T , X1:T (i )) .
p (i
1)

Problem: We do not know how to sample from p ( x1:T j y1:T ).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

128 / 136

Idealized Gibbs Sampler

To sample from p ( , x1:T j y1:T ), an MCMC strategy consists of using the following block Gibbs sampler. At iteration i Sample X1:T (i ) Sample (i )

( x1:T j y1:T ). p ( j y1:T , X1:T (i )) .
p (i
1)

Problem: We do not know how to sample from p ( x1:T j y1:T ).

Naive particle approximation where X1:T (i ) p (x1:T jy1:T , (i )) is b substituted to X1:T (i ) p (x1:T jy1:T , (i )) is obviously incorrect.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

128 / 136

Particle Gibbs Sampler
At iteration i Sample (i ) p ( jy1:T , X1:T (i 1)).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

129 / 136

Particle Gibbs Sampler
At iteration i Sample (i ) Run a conditional SMC algorithm for (i ) consistent with X1:T (i 1) and its ancestral lineage. p ( jy1:T , X1:T (i 1)).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

129 / 136

Particle Gibbs Sampler
At iteration i Sample (i ) Run a conditional SMC algorithm for (i ) consistent with X1:T (i 1) and its ancestral lineage. Sample X1:T (i ) p (x1:T jy1:T , (i )) from the resulting b approximation (hence its ancestral lineage too). p ( jy1:T , X1:T (i 1)).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

129 / 136

Particle Gibbs Sampler
At iteration i Sample (i ) Run a conditional SMC algorithm for (i ) consistent with X1:T (i 1) and its ancestral lineage. Sample X1:T (i ) p (x1:T jy1:T , (i )) from the resulting b approximation (hence its ancestral lineage too). p ( jy1:T , X1:T (i 1)).

Proposition. Assume that the idealGibbs sampler chain is ergodic then under very weak assumptions the particle Gibbs sampler chain is ergodic and admits p ( , x1:T j y1:T ) as an invariant distribution for any N 2.
A. Doucet (MLSS Sept. 2012) Sept. 2012 129 / 136

Nonlinear State-Space Model

Consider the following model Xt Yt where Vt

= =

1 Xt 2

1

+ 25

Xt 1 1 + Xt2

+ 8 cos 1.2t + Vt ,
1

Xt2 + Wt 20

N 0, 2 , Wt v

N 0, 2 and X1 w

N 0, 52 .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

130 / 136

Nonlinear State-Space Model

Consider the following model Xt Yt where Vt

= =

1 Xt 2

1

+ 25

Xt 1 1 + Xt2

+ 8 cos 1.2t + Vt ,
1

Xt2 + Wt 20

N 0, 2 , Wt N 0, 2 and X1 v w Use the prior for fXt g as proposal distribution.

N 0, 52 .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

130 / 136

Nonlinear State-Space Model

Consider the following model Xt Yt where Vt

= =

1 Xt 2

1

+ 25

Xt 1 1 + Xt2

+ 8 cos 1.2t + Vt ,
1

Xt2 + Wt 20

N 0, 2 , Wt N 0, 2 and X1 N 0, 52 . v w Use the prior for fXt g as proposal distribution. For a xed , we evaluate the expected acceptance probability as a function of N.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

130 / 136

Average Acceptance Probability
1 0.9 0.8 0.7

Acceptance Rate

0.6 0.5 0.4 0.3 0.2 0.1 0 0 200 400 600

T= 10 T= 25 T= 50 T=100
800 1000 1200 1400 1600 1800 2000

Number of Particles

Average acceptance probability when 2 = 2 = 10 v w
A. Doucet (MLSS Sept. 2012) Sept. 2012 131 / 136

Average Acceptance Probability
1 0.9 0.8 0.7

Acceptance Rate

0.6 0.5 0.4 0.3 0.2 0.1 0 0 200 400 600

T= 10 T= 25 T= 50 T=100
800 1000 1200 1400 1600 1800 2000

Number of Particles

Average acceptance probability when 2 = 10, 2 = 1 v w
A. Doucet (MLSS Sept. 2012) Sept. 2012 132 / 136

Inference for Stochastic Kinetic Models
Two species Xt1 (prey) and Xt2 (predator) Pr Xt1+dt =xt1+1, Xt2+dt =xt2 xt1 , xt2 = xt1 dt + o (dt ) , Pr Xt1+dt =xt1 1, Xt2+dt =xt2+1 xt1 , xt2 = xt1 xt2 dt + o (dt ) , Pr Xt1+dt =xt1 , Xt2+dt =xt2 1 xt1 , xt2 = xt2 dt + o (dt ) , with
1 Yk = Xk T + Wk with Wk i.i.d.

N 0, 2 .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

133 / 136

Inference for Stochastic Kinetic Models
Two species Xt1 (prey) and Xt2 (predator) Pr Xt1+dt =xt1+1, Xt2+dt =xt2 xt1 , xt2 = xt1 dt + o (dt ) , Pr Xt1+dt =xt1 1, Xt2+dt =xt2+1 xt1 , xt2 = xt1 xt2 dt + o (dt ) , Pr Xt1+dt =xt1 , Xt2+dt =xt2 1 xt1 , xt2 = xt2 dt + o (dt ) , with
1 Yk = Xk T + Wk with Wk i.i.d.

N 0, 2 .

We are interested in the kinetic rate constants = (, , ) a priori distributed as (Boys et al., 2008; Kunsch, 2011)

G(1, 10),

G(1, 0.25),

G(1, 7.5).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

133 / 136

Inference for Stochastic Kinetic Models
Two species Xt1 (prey) and Xt2 (predator) Pr Xt1+dt =xt1+1, Xt2+dt =xt2 xt1 , xt2 = xt1 dt + o (dt ) , Pr Xt1+dt =xt1 1, Xt2+dt =xt2+1 xt1 , xt2 = xt1 xt2 dt + o (dt ) , Pr Xt1+dt =xt1 , Xt2+dt =xt2 1 xt1 , xt2 = xt2 dt + o (dt ) , with
1 Yk = Xk T + Wk with Wk i.i.d.

N 0, 2 .

We are interested in the kinetic rate constants = (, , ) a priori distributed as (Boys et al., 2008; Kunsch, 2011)

G(1, 10),

G(1, 0.25),

G(1, 7.5).

MCMC methods require reversible jumps, Particle MCMC requires only forward simulation.
A. Doucet (MLSS Sept. 2012) Sept. 2012 133 / 136

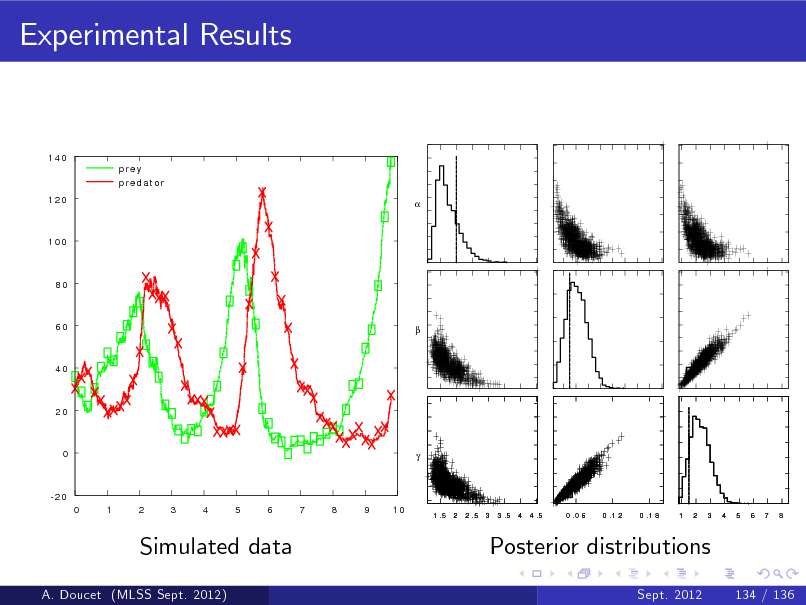
Experimental Results

140 prey predat or 120

100

80

60

40

20

0

-20 0 1 2 3 4 5 6 7 8 9 10
1 .5 2 2 .5 3 3 .5 4 4 .5 0 .0 6 0 .1 2 0 .1 8 1 2 3 4 5 6 7 8

Simulated data
A. Doucet (MLSS Sept. 2012)

Posterior distributions
Sept. 2012 134 / 136

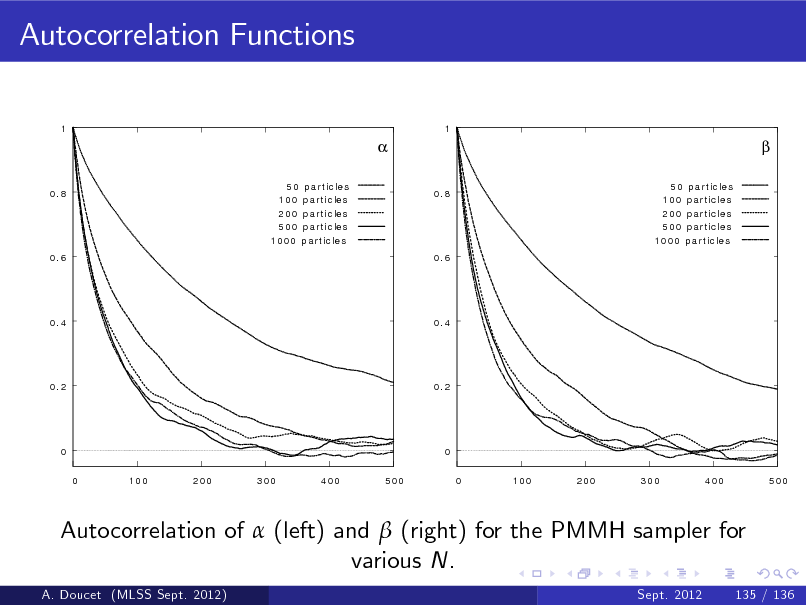
Autocorrelation Functions
1 1

0.8 50 100 200 500 1000 p a r t ic le s p a r t ic le s p a r t ic le s p a r t ic le s p a r t ic le s 0.8 50 100 200 500 1000 p a r t ic le s p a r t ic le s p a r t ic le s p a r t ic le s p a r t ic le s

0.6

0.6

0.4

0.4

0.2

0.2

0 0 100 200 300 400 500

0 0 100 200 300 400 500

Autocorrelation of (left) and (right) for the PMMH sampler for various N.
A. Doucet (MLSS Sept. 2012) Sept. 2012 135 / 136

Summary

O- ine Bayesian parameter inference is feasible by using SMC proposals within MCMC.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

136 / 136

Summary

O- ine Bayesian parameter inference is feasible by using SMC proposals within MCMC. This approach does not suer from degeneracy problem and N scales roughly linearly with T .

A. Doucet (MLSS Sept. 2012)

Sept. 2012

136 / 136

Summary

O- ine Bayesian parameter inference is feasible by using SMC proposals within MCMC. This approach does not suer from degeneracy problem and N scales roughly linearly with T . Particle MCMC allow us to perform Bayesian inference for dynamic models for which only forward simulation is possible.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

136 / 136

Summary

O- ine Bayesian parameter inference is feasible by using SMC proposals within MCMC. This approach does not suer from degeneracy problem and N scales roughly linearly with T . Particle MCMC allow us to perform Bayesian inference for dynamic models for which only forward simulation is possible. Computationally intensive but several implementations on GPU already available and applications in control, ecology, econometrics, biochemical systems, epidemiology, water resources research etc.

A. Doucet (MLSS Sept. 2012)

Sept. 2012

136 / 136

Summary

O- ine Bayesian parameter inference is feasible by using SMC proposals within MCMC. This approach does not suer from degeneracy problem and N scales roughly linearly with T . Particle MCMC allow us to perform Bayesian inference for dynamic models for which only forward simulation is possible. Computationally intensive but several implementations on GPU already available and applications in control, ecology, econometrics, biochemical systems, epidemiology, water resources research etc. Selection of N is a key issue and some guidelines are available (Lee, Andrieu & D., 2012), (D., Pitt & Kohn, 2012).

A. Doucet (MLSS Sept. 2012)

Sept. 2012

136 / 136