Submodular Optimization and Approximation Algorithm
Satoru Iwata RIMS, Kyoto University

Outline
Submodular Functions Examples Discrete Convexity Submodular Function Minimization Approximation Algorithms Submodular Function Maximization Approximating Submodular Functions

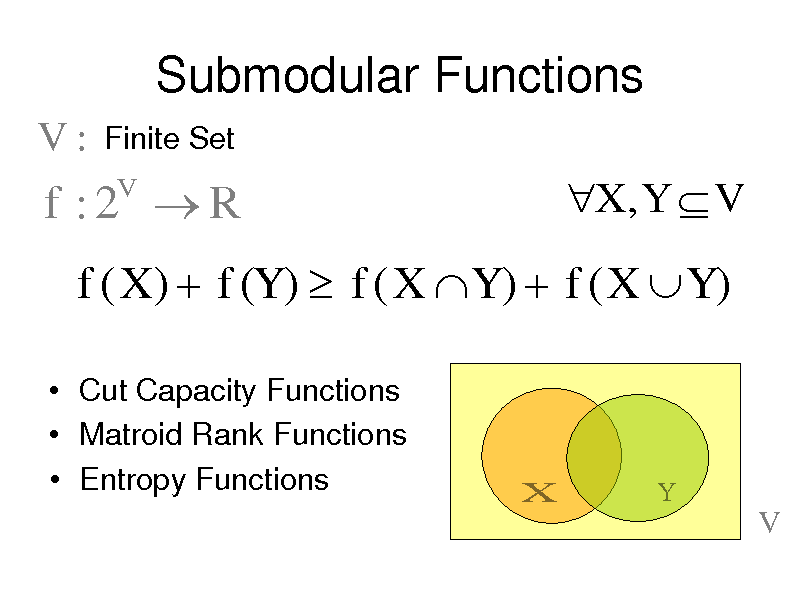
Submodular Functions
V:
Finite Set
V

f :2 R

X , Y V

f ( X ) f (Y ) f ( X Y ) f ( X Y )
Cut Capacity Functions Matroid Rank Functions Entropy Functions

X

Y

V

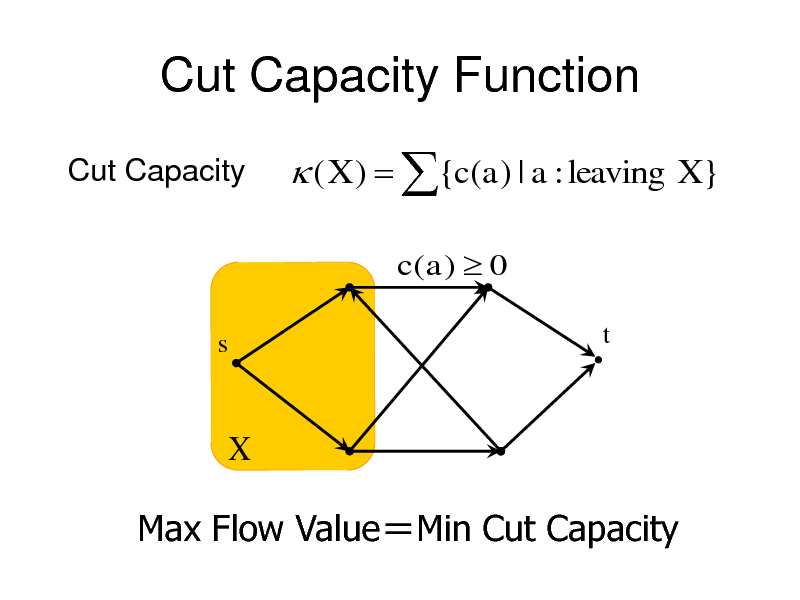
Cut Capacity Function
Cut Capacity

( X ) {c(a) | a : leaving X }
c( a ) 0

s

t

X

Max Flow ValueMin Cut Capacity

Matroid Rank Functions
Matrix Rank Function Whitney (1935)

( X ) rank A[U , X ]
X

A
V

U

X V , ( X ) | X | X Y ( X ) (Y ) : Submodular

Entropy Functions
Information Sources

h( ) 0

h(X ) : Entropy of the Joint Distribution
h( X ) h(Y ) h( X Y ) h( X Y )
X
Conditional Mutual Information

0

Positive Definite Symmetric Matrices
X

f ( ) 0
A
A[X ] f ( X ) log det A[ X ]
Ky Fans Inequality

f ( X ) f (Y ) f ( X Y ) f ( X Y )
Extension of the Hadamard Inequality
det A Aii
iV

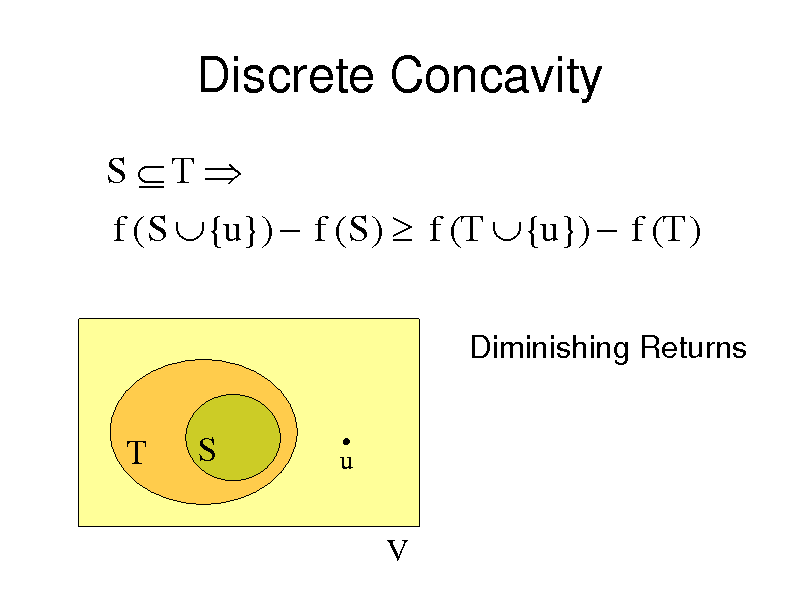
Discrete Concavity
S T f ( S {u}) f ( S ) f (T {u}) f (T )
Diminishing Returns

T

S

u

V

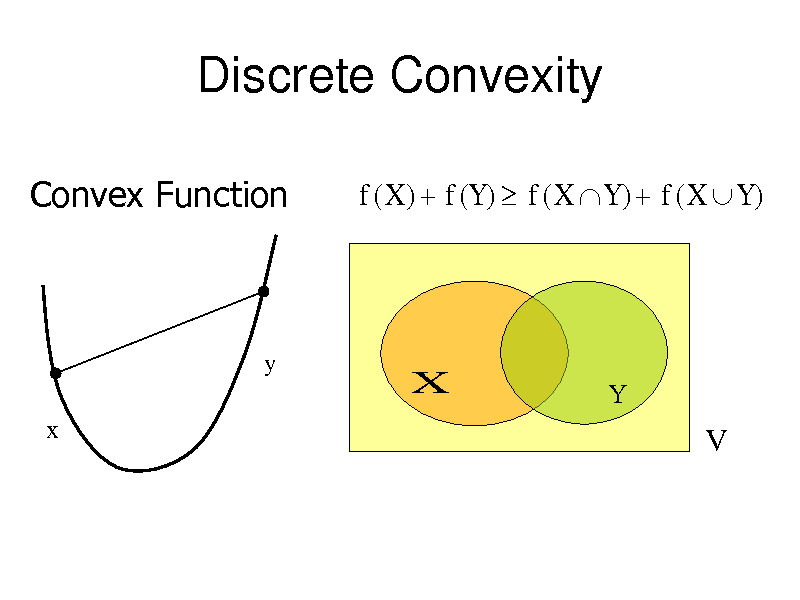
Discrete Convexity
Convex Function
f ( X ) f (Y ) f ( X Y ) f ( X Y )

y

X

Y

x

V

Discrete Convexity
V {a, b, c}
{a, b}
{b, c}
Lovsz (1983)

f Linear Interpolation

{b}

f Convex
{c}

{a}

f Submodular

[0,1] : Chosen Uniformly at Random f ( x) E[ f ( X )] X : {v | x(v) },

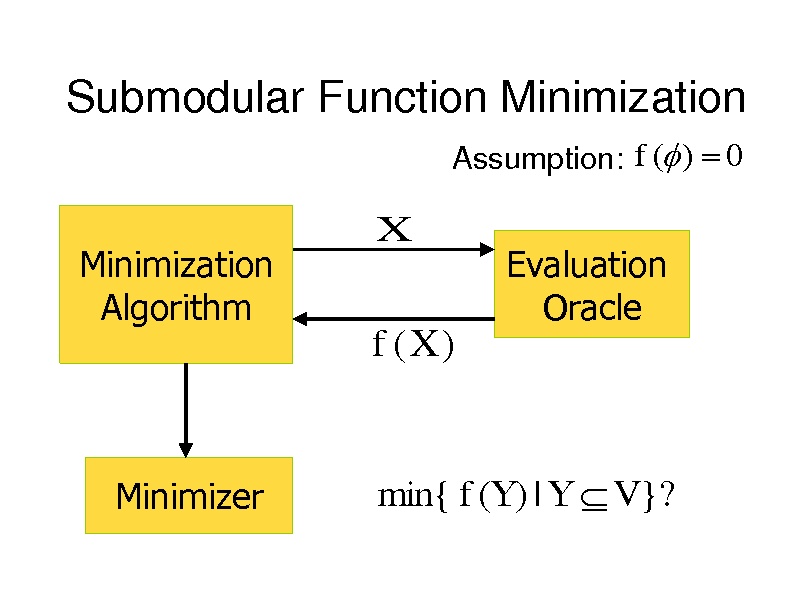
Submodular Function Minimization
Assumption: f ( ) 0

Minimization Algorithm

X

Evaluation Oracle

f (X )

Minimizer

min{ f (Y ) | Y V }?

Submodular Function Minimization
Grtschel, Lovsz, Schrijver (1981, 1988)
Ellipsoid Method

O(n5 log M ) O(n7 log n)

Cunningham (1985)

O( n 7 n 8 )
Schrijver (2000)

Iwata, Fleischer, Fujishige (2000)

: Time for Function Evaluation

M max | f ( X ) |
X V

Base Polyhedra
R {x | V R}
V

x(Y ) x(v)
vY

Submodular Polyhedron

P( f ) {x | x R , Y V , x(Y ) f (Y )}
V

Base Polyhedron

B( f ) {x | x P( f ), x(V ) f (V )}

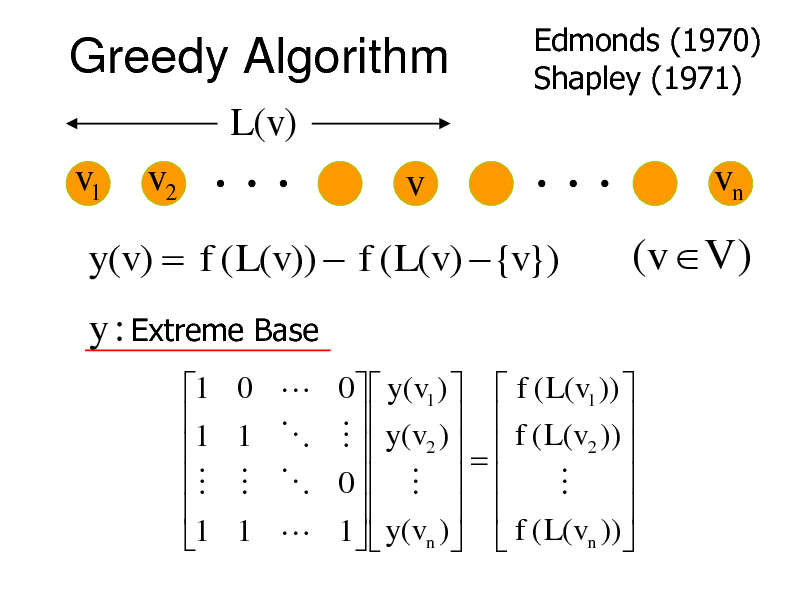
Greedy Algorithm
L(v)

Edmonds (1970) Shapley (1971)

v1

v2

v

vn

y(v) f ( L(v)) f ( L(v) {v})

(v V )

y : Extreme Base
1 1 1 0 1 1 0 y (v1 ) f ( L(v1 )) y (v ) f ( L(v )) 2 2 0 1 y (vn ) f ( L(vn ))

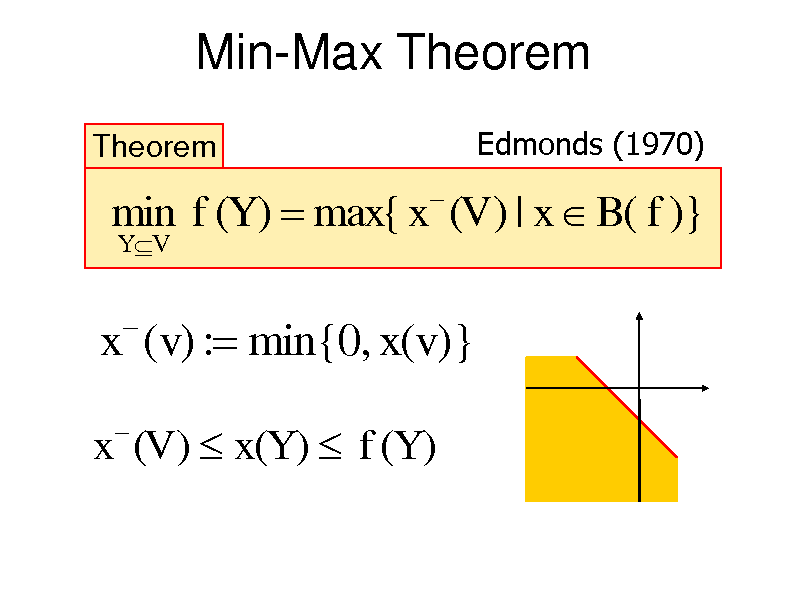
Min-Max Theorem
Theorem
Y V

Edmonds (1970)

min f (Y ) max{ x (V ) | x B( f )}

x (v) : min{0, x(v)}
x (V ) x(Y ) f (Y )

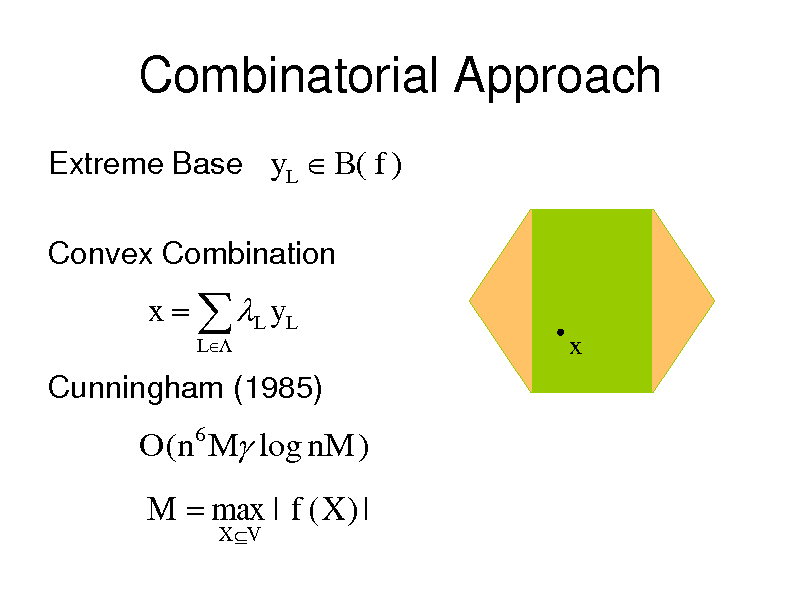
Combinatorial Approach
Extreme Base yL B( f )
Convex Combination

x L y L
L

x

Cunningham (1985)

O(n6 M log nM )

M max | f ( X ) |
X V

Combinatorial Approach
x L y L
L

L

y L : Extreme Base

x(v) 0, v T x(v) 0, v T

T

yL (T ) f (T ), L . x(T ) f (T ).
x (V ) x(T ) f (T )

T : Minimizer

Submodular Function Minimization
Grtschel, Lovsz, Schrijver (1981, 1988)
Ellipsoid Method

O(n5 log M ) O(n7 log n)

Cunningham (1985)

O( n 7 n 8 )
Schrijver (2000)
Fleischer, Iwata (2000)

Iwata, Fleischer, Fujishige (2000)

Iwata (2002)
Fully Combinatorial

Iwata (2003)

Orlin (2007)

O((n 4 n5 ) log M )
Iwata, Orlin (2009)

O(n5 n6 )

The Fujishige-Wolfe Algorithm
Minimize x
2

Fujishige (1984)

subject to x B( f )

x : opt.sol.
S : {v | x (v) 0}
T : {v | x (v) 0}

x

Minimal Minimizer Maximal Minimizer

f (S ) f (T ) min f ( X )
X V

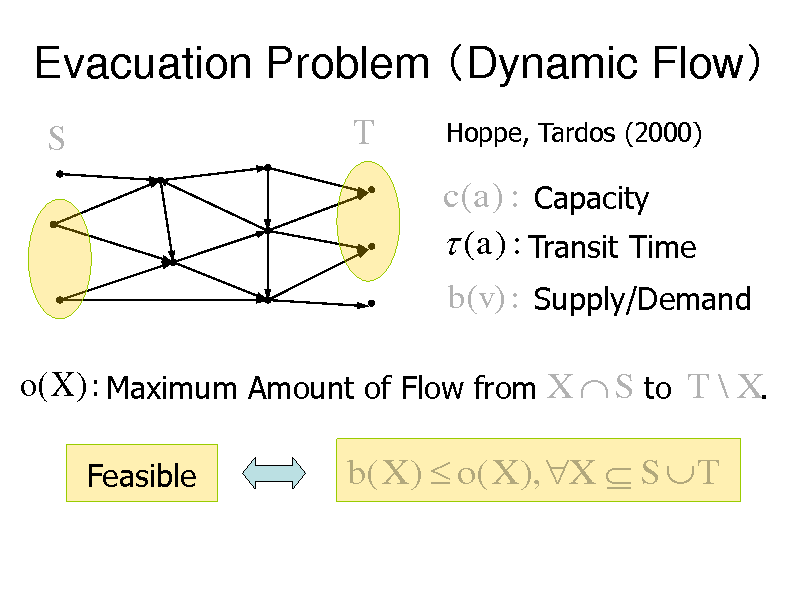
Evacuation Problem Dynamic Flow
S
T
Hoppe, Tardos (2000)

c(a) : Capacity (a) : Transit Time
b(v) : Supply/Demand

o(X ) : Maximum Amount of Flow from X S to T \ X.
Feasible

b( X ) o( X ), X S T

Multiterminal Source Coding
RY

X

Encoder
Encoder

RX

Y

RY

Decoder

H ( X ,Y )
H (Y )

H (Y | X )

Slepian, Wolf (1973)
H(X | Y)
H (X ) H ( X , Y )

RX

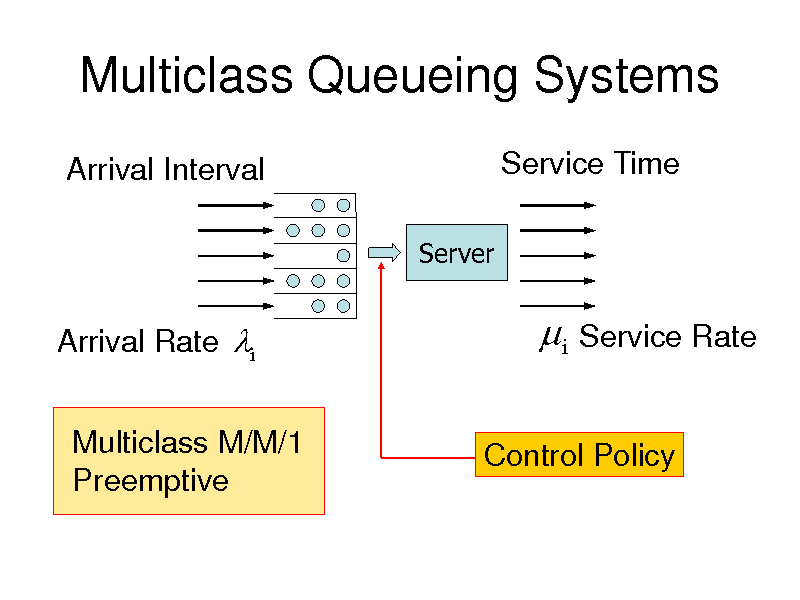
Multiclass Queueing Systems
Arrival Interval
Server

Service Time

Arrival Rate i Multiclass M/M/1 Preemptive

i Service Rate
Control Policy

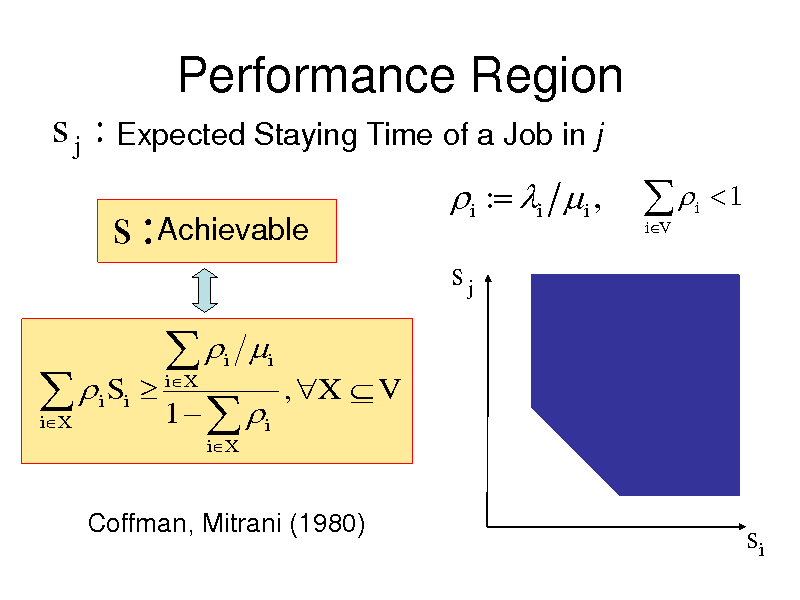
Performance Region
s j : Expected Staying Time of a Job in j

s : Achievable
i Si
iX

i : i i ,
sj
RY
s:

iV

i

1

1
iX i iX

i

, X V

i

Coffman, Mitrani (1980)

si

A Class of Submodular Functions
x, y, z RV
Itoko & Iwata (2007)

h : Nonnegative, Nondecreasing, Convex

f ( X ) z( X ) y( X )h( x( X ))
Submodular

(X V )

i Si
iX

1
iX i iX

i

zi : i Si
, X V

i yi : i
1 h( x) : 1 x

i

xi : i

Zonotope in 3D
w( X ) ( x( X ), y( X ), z( X ))

z

Z conv{w( X ) | X V }
Zonotope

~ f ( x, y, z ) z yh( x)
min{ f ( X ) | X V } ~ min{ f ( x, y, z ) | ( x, y, z ) : Lower Extreme Point of Z }

~ Remark: f ( x, y, z ) is NOT concave!

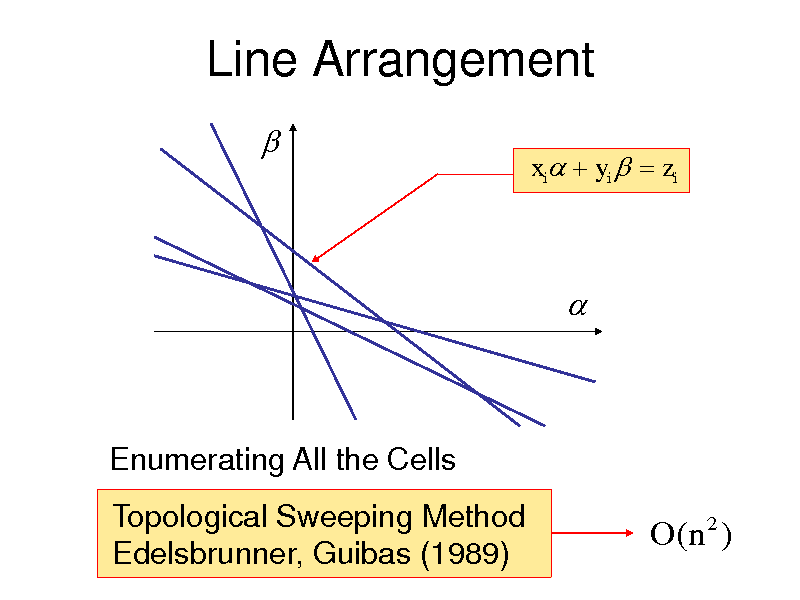
Line Arrangement

xi yi zi

Enumerating All the Cells Topological Sweeping Method Edelsbrunner, Guibas (1989)

O( n 2 )

Symmetric Submodular Functions
f :2 R
V

Symmetric

f ( X ) f (V \ X ),

X V .

Symmetric Submodular Function Minimization

min{ f ( X ) | X V }?
O(n3 ) Queyranne (1998)
Minimum Cut Algorithm by MA-ordering Nagamochi & Ibaraki (1992) Minimum Degree Ordering Nagamochi (2007)

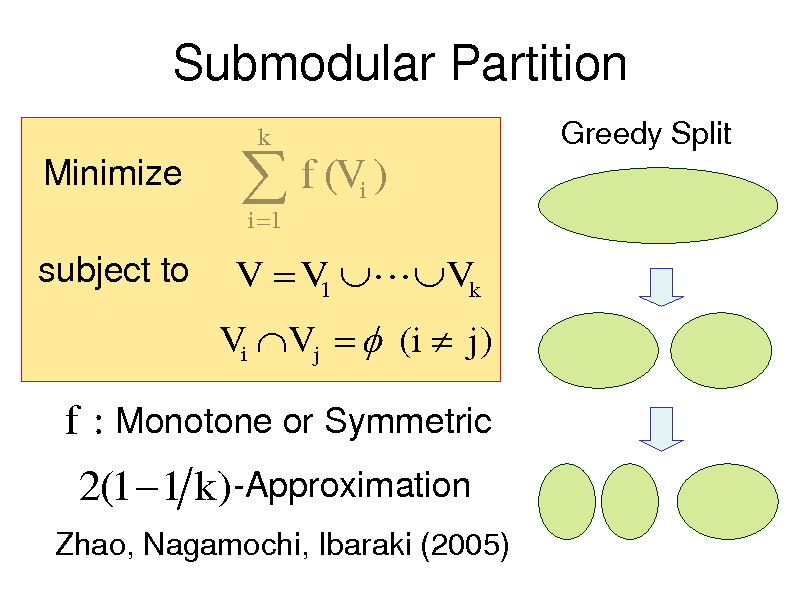
Submodular Partition
Minimize subject to

f (V )
i 1 i

k

Greedy Split

V V1 Vk
Vi V j (i j )

f : Monotone or Symmetric

2(1 1 k )-Approximation
Zhao, Nagamochi, Ibaraki (2005)

Questions
What Kind of Approximation Algorithms Can Be Extended to Optimization Problems with Submodular Cost or Constraints ?
Cf. Submodular Flow (Edmonds & Giles, 1977)

How Can We Exploit Discrete Convexity in Design of Approximation Algorithms?
Cf. Ellipsoid Method (Grtschel, Lovsz & Schrijver, 1981)

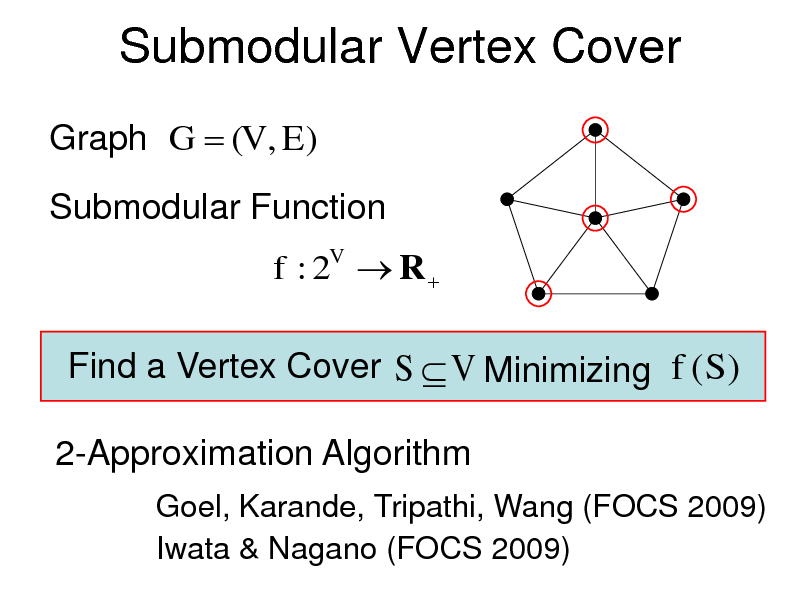
Submodular Vertex Cover
Graph G (V , E )
Submodular Function
f : 2V R

Find a Vertex Cover S V Minimizing f (S ) 2-Approximation Algorithm
Goel, Karande, Tripathi, Wang (FOCS 2009) Iwata & Nagano (FOCS 2009)

Relaxation Problem
Convex Programming Relaxation (CPR)

Minimize

f ( x)

subject to x(u) x(v) 1 (e (u, v) E)
x(v) 0 (v V )

CPR has a half-integral optimal solution. 2-Approximation Algorithm

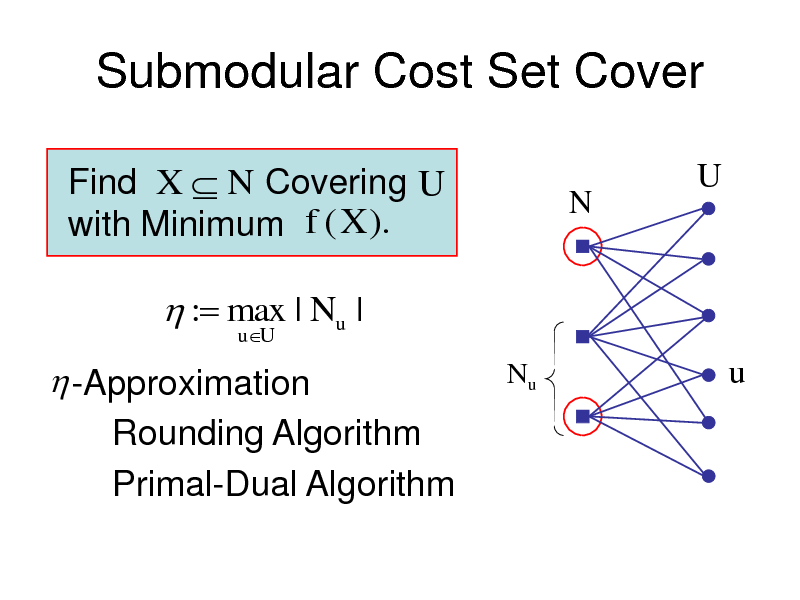
Submodular Cost Set Cover
Find X N Covering U with Minimum f (X ).
N

U

: max | Nu |
uU

-Approximation Rounding Algorithm Primal-Dual Algorithm

Nu

u

Submodular Multiway Partition
Chekuri & Ene (FOCS 2011)

Minimize

f (V )
i 1 i

k

subject to V V1 Vk

Vi V j (i j )

si Vi

(i 1,..., k )

f : Nonnegative Submodular

Relaxation Problem
Convex Programming Relaxation

Minimize
subject to

i 1 k

k

f ( xi )
i

x (v ) 1
i 1

(v V )

xi (si ) 1 (i 1,..., k )
xi (v) 0
Ellipsoid Method

(i 1,..., k , v V )

xi : Optimal Solution

Rounding Scheme
f : Symmetric Submodular
[0,1] : Chosen Uniformly at Random
Ai : {v | xi (v) } (i 1,..., k ),
Uncross ( A1 ,..., Ak )

U : V Ai
i 1

k

Return ( A1 ,..., Ak 1 , Ak U ) 3/2-Approximate Solution

Rounding Scheme
f : Nonnegative Submodular
( 1 ,1] : Chosen Uniformly at Random 2
Ai : {v | xi (v) } (i 1,..., k ),
Return ( A1 ,..., Ak 1 , Ak U )
2-Approximate Solution Improvement over the (k 1) -Approximation by Zhao, Nagamochi, & Ibaraki (2005)

U : V Ai
i 1

k

Submodular Function Maximization
Monotone Submodular Functions
Nemhauser, Wolsey, Fisher (1978) Cardinality Constraint (1-1/e)-Approximation

Calinescu, Chekuri, Pl, Vondrk (IPCO 2007) Vondrk (STOC 2008) Filmes and Ward (FOCS 2012) Matroid Constraint (1-1/e)-Approximation

Greedy Approximation Algorithm
Nemhauser, Wolsey, Fisher (1978)

f : Monotone Submodular Function
Maximize f (S ) subject to | S | k Greedy Algorithm
v1
v j 1

T0 : T j : T j 1 {v j }

T j 1

v j : arg max f (T j 1 {v})

j 1,..., k

Greedy Approximation Algorithm
S : Optimal Solution : f (S )
*
*

k j i ( j 1,..., k )
i 1

j 1

j : f (T j ) f (T j 1 )

f (Tk ) i
i 1

k

) f ( S ) f ( S T j 1 )
* *

f (T j 1 )

uS * \T j 1

f (T

j 1

{u}) f (T j 1 )
j 1

f (T j 1 ) k j

i 1

i

Greedy Approximation Algorithm
Minimize

i 1

k

i

i 1

k

i

f (Tk )
*

subject to

k 0 0 1 1 k 2 0 1 1 k k

: f (S )
j :

1 1 k k

j

j 0
k

( j 1,..., k )

( j 1,..., k )

1 k 1 i 1 1 k 1 e i 1

Submodular Welfare Problem
Utility Functions

f1 ,..., f k (Monotone, Submodular)

Maximize subject to

f (V )
i 1 i i

k

V V1 Vk
Vi V j (i j )

(1 1 e) -Approximation

Vondrk (2008)

Submodular Function Maximization
Nonnegative Submodular Functions
Feige, Mirrokni, Vondrk (FOCS 2007) 2/5-Approximation Lee, Mirrokni, Nagarajan, Sviridenko (STOC 2009) 1/4-Approximation (Matroid Constraint) 1/5-Approximation (Knapsack Constraints) Buchbinder, Feldman, Naor, Schwartz (FOCS 2012) 1/2-Approximation

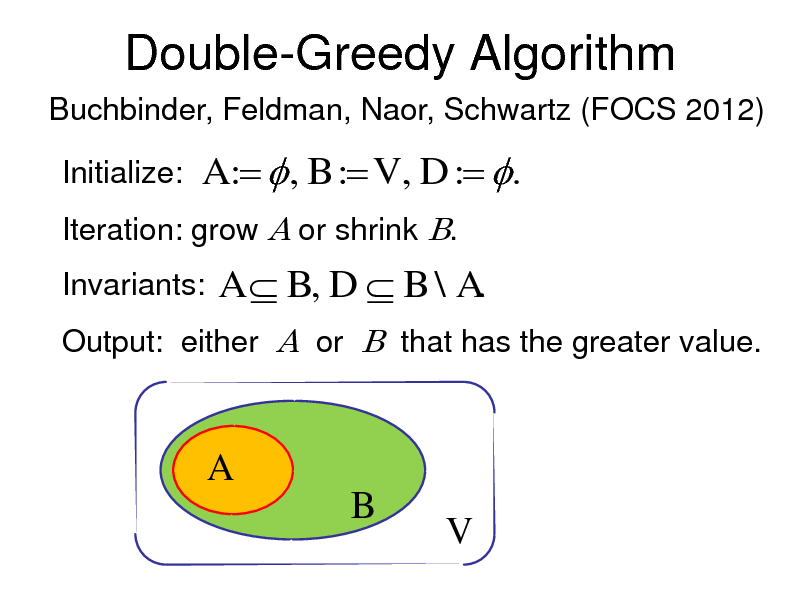
Double-Greedy Algorithm
Buchbinder, Feldman, Naor, Schwartz (FOCS 2012)

Initialize:

A : , B : V , D : . A B, D B \ A.

Iteration: grow A or shrink B. Invariants: Output: either A or B that has the greater value.

A B
V

Double-Greedy Algorithm
While

A D B Select u B \ ( D A). : max{ f ( A {u}) f ( A),0}. : max{ f ( B \ {u}) f ( B),0}.
If

0,

then

A : A {u} with probability B : B \ {u} with probability
Else

,

.

D : D {u}.

Double-Greedy Algorithm
The expectation

E[ f ( A) f ( B) 2 f (Z )]

never decreases in the process.

) Expected changes of f ( A) f ( B) 2 f (Z )
at each iteration is at least

2 ( ) 0.
2

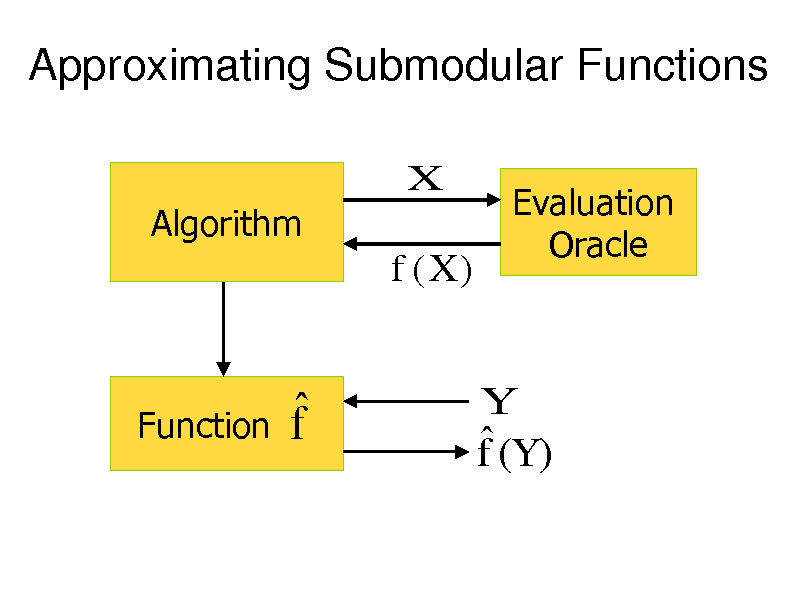
Approximating Submodular Functions
X
Algorithm

f (X )

Evaluation Oracle

Function

f

f (Y )

Y

Approximating Submodular Functions
Goemans, Harvey, Iwata & Mirrokni (SODA 2009)

f ( ) 0, f ( X ) 0, X V . Construct a set function f such that
f ( X ) f ( X ) (n) f ( X ), X V .
For what function is this possible? Algorithm with (n) O( n log n) for monotone submodular functions

Ellipsoidal Approximation
K : Centrally Symmetric Convex Body (x K x K )

E (A) : Maximum Volume Inscribed Ellipsoid
(The John Ellipsoid)

E ( A) K n E ( A)

Submodular Load Balancing
Svitkina & Fleischer (FOCS 2008)

f1 ,..., f m : Monotone Submodular Functions
{V1 ,..., m } V

min max f j (V j ) ?
j

f j ( X ) : p j (v)
vX

Scheduling 2-Approximation Algorithm Lenstra, Shmoys, Tardos (1990)

O( n log n) -Approximation Algorithm

Learning Submodular Functions
Balcan & Harvey (STOC 2010)

PMAC-learning

Construct a set function f such that f ( X ) f ( X ) (n) f ( X )
holds for most (1 fraction) of X . For what function is this possible with probability 1 in poly(n,1 / ,1 / ) time?

Summary
Submodular Functions Arise Everywhere. Discrete Analogue of Convexity. Combinatorial Algorithms for Minimization. Exploit Special Structures of Problems. Approx. Algorithms by Discrete Convexity Approx. Algorithms for Maximization Learning Submodular Functions